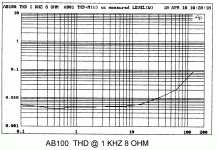
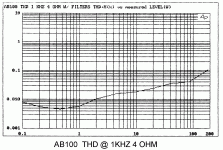
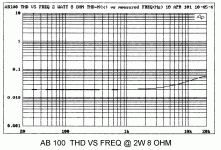
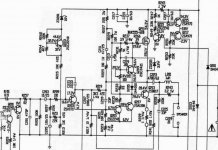
High Output Subs that play 20Hz to ≥200Hz
- By camplo
- Subwoofers
- 296 Replies
Hi yall, I'm hoping to create a space to talk about subwoofers that reach higher than typically expected, all the while covering down 20hz/30hz without sacrificing the accuracy of its upper passband. Sealed enclosures with multiple large woofers, and high xmax are a good choice. Having pairs of these types of subs only makes things better and being that we are traveling into the realm of localization by playing so high, these types of subs are to be apart of the mains, either by proximity or appendage.
Sealed enclosures as described above make short work of the task... I'd consider something like a large sealed cab, dual 18" with >14mm xmax the status quo. Where it gets interesting is transmission line and bass reflex. Vented Designs need to be a lot more particular. Damping is needed but maybe not in every design. A front loaded horn like the known HT tuba which is an bandpass design where the front horn is entered in offset, may do well thanks to the near 0 CSA at the beginning of the line. Of course it comes with its own sets of pros and cons, the line length creates delay, for example.
I will post some designs that fit the category, and I hope that you guys have some designs that you like as well. There are details that help optimize these types of subs, lets chop it up at our leisure

Sealed enclosures as described above make short work of the task... I'd consider something like a large sealed cab, dual 18" with >14mm xmax the status quo. Where it gets interesting is transmission line and bass reflex. Vented Designs need to be a lot more particular. Damping is needed but maybe not in every design. A front loaded horn like the known HT tuba which is an bandpass design where the front horn is entered in offset, may do well thanks to the near 0 CSA at the beginning of the line. Of course it comes with its own sets of pros and cons, the line length creates delay, for example.
I will post some designs that fit the category, and I hope that you guys have some designs that you like as well. There are details that help optimize these types of subs, lets chop it up at our leisure