Bias issue
- Solid State
- 7 Replies
So working with brand new amplifier big and famous that had a customer complain about sound
initial test proved the amp was too cold
Checked bias according to the manufacturer and found low ....
Manufacturer need 8mv per transistor but found only 2.5
So adjusted bias and all appears to work fine .....
Placed a question to the chief engineer ( Turkish ) ( ?????? ) about it, since this is not only famous but also very expensive amp
And the answer was that may be from transportation trimmers have been moved Trimmers areBB top quality 10
turn
Please comment your opinion for this bellow
initial test proved the amp was too cold
Checked bias according to the manufacturer and found low ....
Manufacturer need 8mv per transistor but found only 2.5
So adjusted bias and all appears to work fine .....
Placed a question to the chief engineer ( Turkish ) ( ?????? ) about it, since this is not only famous but also very expensive amp
And the answer was that may be from transportation trimmers have been moved Trimmers areBB top quality 10
Please comment your opinion for this bellow
Custom audio transformers - input, DAC/MC, interstage, output
- By Dorin Bodea
- Vendor's Bazaar
- 4 Replies
Just in case you need a custom audio transformer like the one in attach you can contact me and if it's doable then you can have what you won't find in other places.
I use mainly mumetal/permalloy and HiB/GOSS and you can see some results in the FB page attached, where I list from time to time some of my projects, you don't need an account.
https://www.facebook.com/profile.php?id=100057288107123
I'm located in Europe, but in the last 20 years I've sent my xfmrs pretty much all aver the world 🙂
I use mainly mumetal/permalloy and HiB/GOSS and you can see some results in the FB page attached, where I list from time to time some of my projects, you don't need an account.
https://www.facebook.com/profile.php?id=100057288107123
I'm located in Europe, but in the last 20 years I've sent my xfmrs pretty much all aver the world 🙂
Pure Tube i/V for ES9038PRO-9028, 9018, AKM...
- By quanghao
- Group Buys
- 114 Replies
Hello all friends!
After many years of using ES chips, we have experienced with DAC, ES9018S, ES9038PRO.
We are glad to announce to you that we have succeeded in designing the output for ES9038PRO, undergoing over 15 different designs, we chose the best design to share for you. Yes, you can make yourself a DAC with pure tube output.
I call it: Pure Tube i / V balanced.
Andrea-Quanghao-Morten would like to share our design with you!
Sincerely thank you.
1. Pure tube I/V- Balanced Output
Pure tube I/V PCB
Best design from our 15 design IV.
You can use for:
ES9038 DAC
ES9028...
AKM4497.....
♥ PCB dimension: 19.5 x 19cm
♥ PCB thickness: 1.6mm, double layer,
2oz copper.
♥ Symmetric layout design and signal paths with minimum
parasitic.
♥ Dedicated ground and power rails layout design.
Tube need use :
♥ Input: 2 x 12AU7
♥ Output: 2 x 6DJ8 or E88CC
♥ Cap Output: 4 x 1µF
♥ Simple R/IV
price: 45$
EX:
And Pure i/V schematic L:
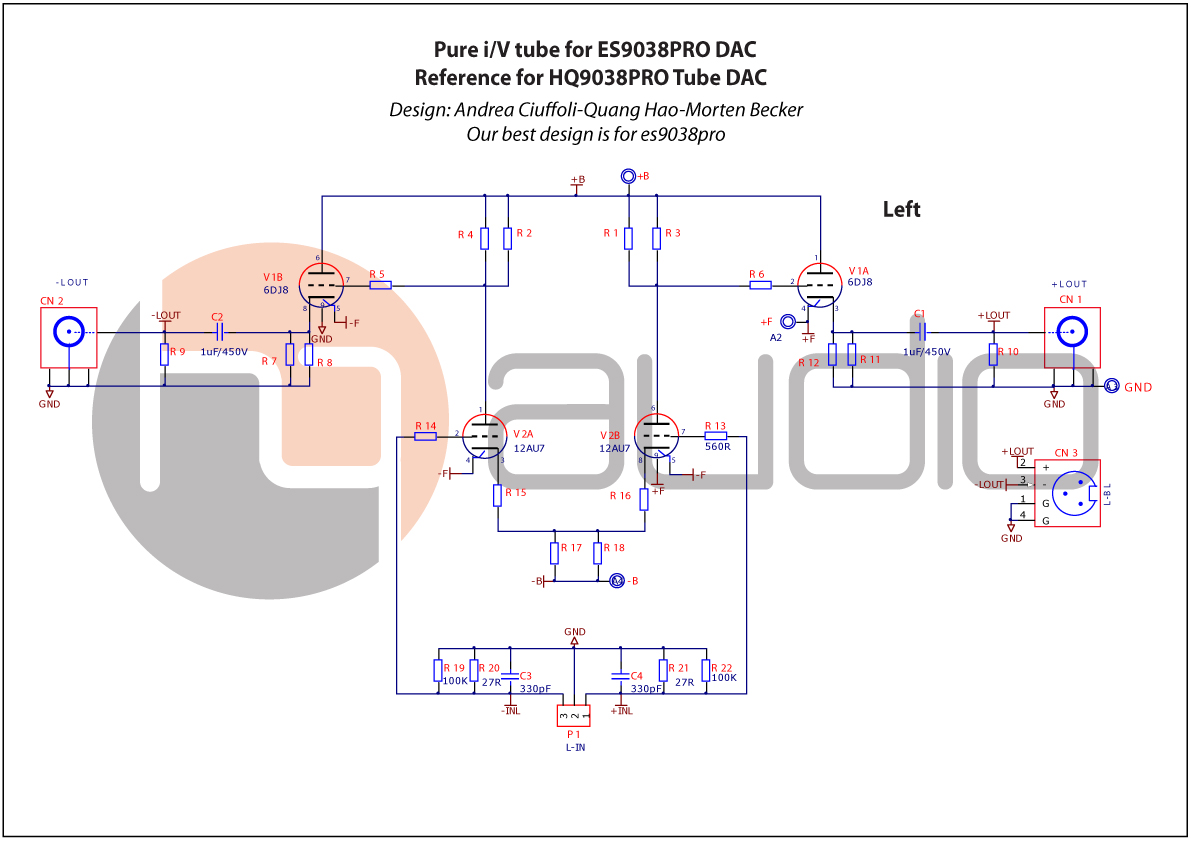
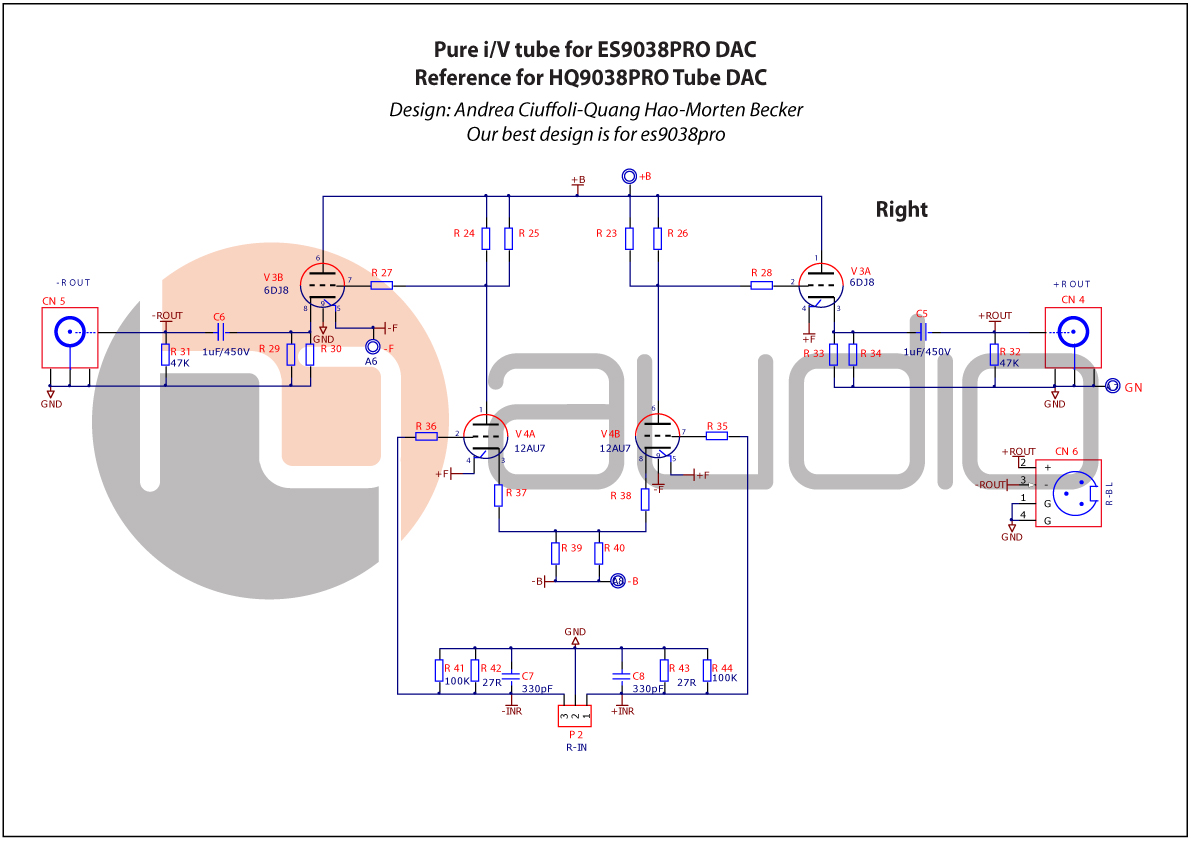
And Pure i/V schematic R:
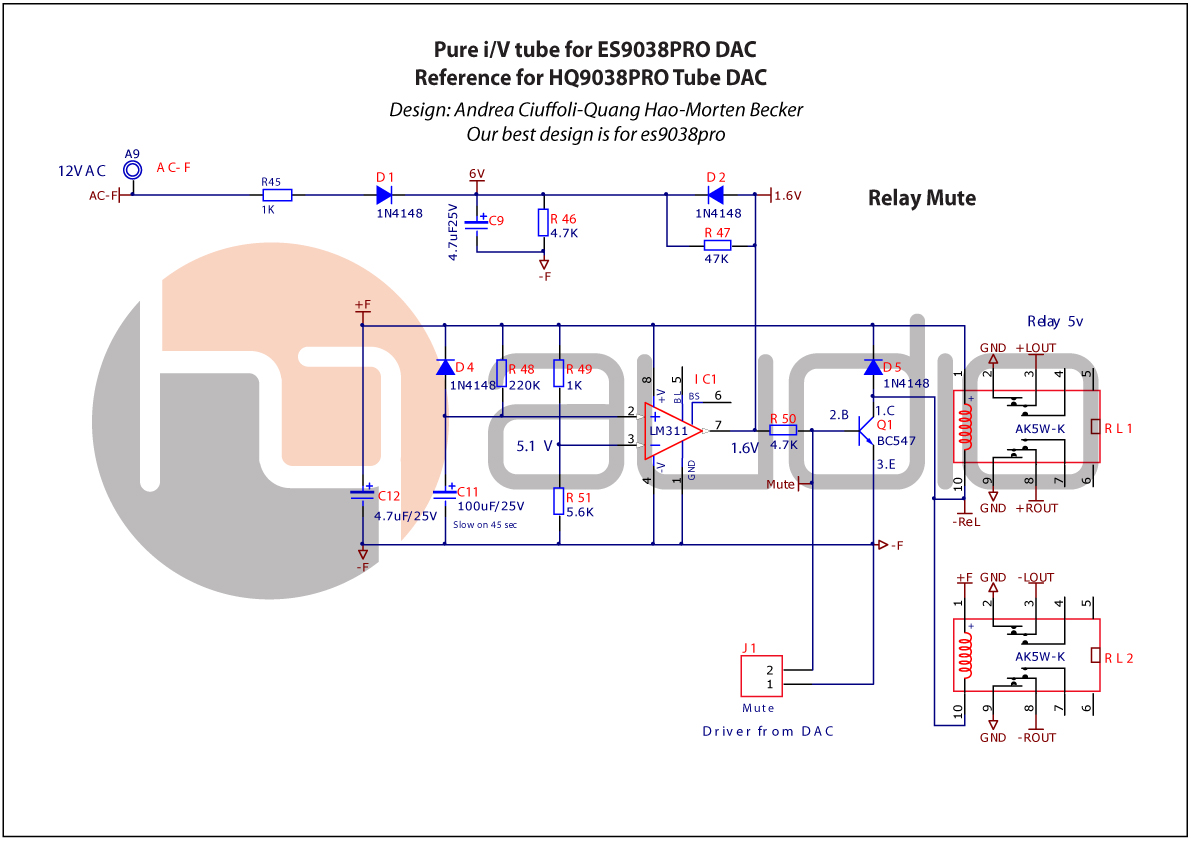
And Pure i/V schematic Relay:
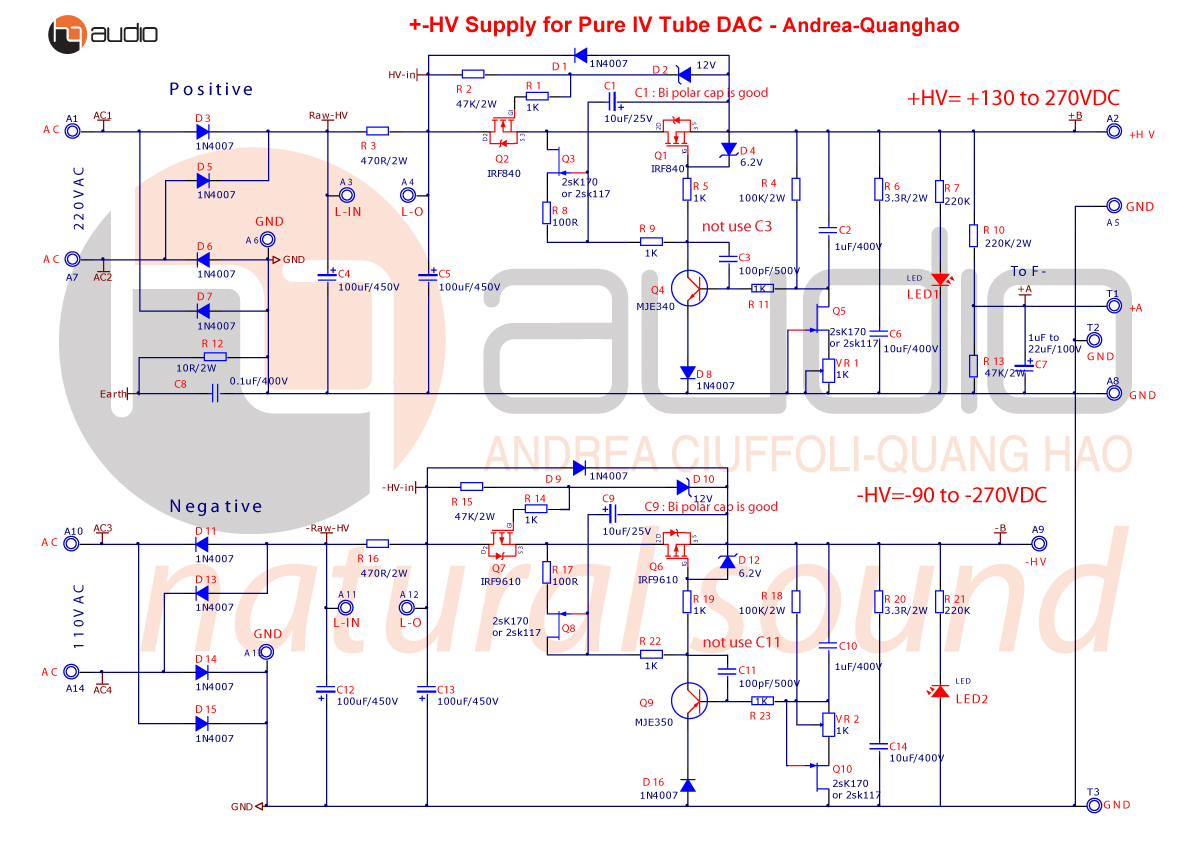
2. HQ-Hv Supply for Tube IV
Output:
1. Positive voltage:
♥ 100-270VDC.
2. Negative voltage:
♥ 100-270VDC.
♥ Low noise , Low Z-out
♥ Use mosfet
3. Filemant Tube: 6.3VDC
to 12VDC/3A.
price: 35$
And Hq-hv schematic:
And schematic Filemant
Shipping by transport envelope for all countryll contry: 25$.
Payment by paypal: quanghao168@yahoo.com.vn
Paypal free: 2%.
After many years of using ES chips, we have experienced with DAC, ES9018S, ES9038PRO.
We are glad to announce to you that we have succeeded in designing the output for ES9038PRO, undergoing over 15 different designs, we chose the best design to share for you. Yes, you can make yourself a DAC with pure tube output.
I call it: Pure Tube i / V balanced.
Andrea-Quanghao-Morten would like to share our design with you!
Sincerely thank you.
1. Pure tube I/V- Balanced Output
Pure tube I/V PCB
Best design from our 15 design IV.
You can use for:
ES9038 DAC
ES9028...
AKM4497.....
♥ PCB dimension: 19.5 x 19cm
♥ PCB thickness: 1.6mm, double layer,
2oz copper.
♥ Symmetric layout design and signal paths with minimum
parasitic.
♥ Dedicated ground and power rails layout design.
Tube need use :
♥ Input: 2 x 12AU7
♥ Output: 2 x 6DJ8 or E88CC
♥ Cap Output: 4 x 1µF
♥ Simple R/IV
price: 45$
EX:
And Pure i/V schematic L:
And Pure i/V schematic R:
And Pure i/V schematic Relay:
2. HQ-Hv Supply for Tube IV
Output:
1. Positive voltage:
♥ 100-270VDC.
2. Negative voltage:
♥ 100-270VDC.
♥ Low noise , Low Z-out
♥ Use mosfet
3. Filemant Tube: 6.3VDC
to 12VDC/3A.
price: 35$
And Hq-hv schematic:
And schematic Filemant
Shipping by transport envelope for all countryll contry: 25$.
Payment by paypal: quanghao168@yahoo.com.vn
Paypal free: 2%.
"The (Barrie) Gilbert Paper" "Are OP Amps Really Linear"
- By PB2
- Solid State
- 6 Replies
We discussed this paper over a decade ago and it was online at the time but, today, I had to use the Wayback Machine
to find it. Making it a thread here so that it is not lost forever. I believe that there was also a .pdf of it. Most of the
theory also applies to power amps.
There are a few Figures that were not captured.
A few very old links where it was discussed:
This one is almost 20 years old:
https://www.diyaudio.com/community/...rning-cordell-otala-and-gilbert-papers.48873/
Fairly certain that it was referenced here also, not saying that this is a good thread but here it is:
https://www.diyaudio.com/community/threads/whats-your-reasoning-and-not-whats-your-belief.41770/
Everyone knows that op amps are the most linear building blocks in the analog repertoire. If you want nonlinear behavior, you had better look to multipliers or other arcania. But we recognize that every real amplifier has a bit of nonlinearity, like it or lump it, so maybe we ought to take a look at just how good is that standard op amp, the voltage-mode amplifier identified as an 'OPA' in previous columns, when used at frequencies above a few Hertz.
It wasn't so many years ago, in the heyday of the uA741, that a guy called Otala discovered this early 1-MHz OPA performed a lot worse than might expected at audio frequencies, so he wrote a paper in the Journal of the Audio Engineering Society in which he coined a brand new term -- transient intermodulation distortion, or 'TIM' -- to describe in audio lingo what most users of op amps had already discovered, namely, the little matter of a limited slew-rate. It was a phenomenon peculiar to IC op amps. If you had grown up with vacuum tubes, you had plenty of reason to raise your eyebrows, since, unlike bipolar transistors (with their extremely high gm and a correspondingly small range over which linearity prevails in the familiar differential-pair gain cell), tube amplifiers rarely, if ever, got themselves into this pathological state of affairs.
Predictably, Otala's 'discovery' only added welcome fuel to the fire of those who were quite convinced that these new-fangled transistor amplifiers were genetically incapable of pleasing the audiophile ear, a notion which, like all myths, persists unabated, in spite of the fact that the root cause of TIM is now completely understood, and can easily be avoided in transistor amplifiers expressly designed for the most demanding audio applications. Nevertheless, Mister Otala was on to something, and although there are many splendid op amps out there, not all deliver quite what the textbooks promise. Accordingly, for a few minutes, we will examine a major source of distortion in op amps. Writing this in Kailua-Kona, Hawaii, with the thunder of the surf just feet away from this lanai, as the palms and hibiscus breathe the balmy post-dawn air, I have ample time on my hands.
The dominant mantra intoned over the application of op amps goes something like this: Never mind what's inside that cute little triangle; the function of the overall linear block -- invariably just a simple amplifier or filter stage -- is determined (almost entirely) by the passive components that are added to provide feedback. The triangle thing is merely the power-house that, come rain or shine, makes everything work out right in the end, by a kind of op-amp magic. The parenthetical inclusion is a concession to those who know a bit better, and it's the focus of this piece.
Reduced to essentials, most voltage-mode op amps, OPAs, are based on a topology like that shown in Fig. 1. To develop the theory, our device is here connected as a simple amplifier with a closed-loop gain of G, determined by the ratio (R1+R2)/R2, which can alternatively be expressed in terms of the feedback fraction b = 1/G. Because the dominant source of nonlinearity is in the input cell, the distortion will be lowest in the voltage-follower mode.
In the interests of clarity and analytical simplicity, we will assume here that the output is a perfect sinusoid, having an amplitude E and angular frequency w, that is, Esinwt, and work backwards from this output to deduce what VIN would need to be to generate that output. This may seem an odd approach, and it's certainly not essential to do it this way. However, many analyses involving the exponential behavior of transistors lead to transcendental solutions when pursued in the forward direction, and that's true in this case. A reverse-direction analysis quickly generates the key insights, and points towards the required modifications to effect a solution, at the price of a slight but not serious loss of rigor.
A bipolar implementation is shown, since many monolithic OPAs use this technology. A basic differential-pair Q1, Q2, also cast in pnp form, and having a near-perfect current-source IT in its 'tail', senses the difference between the applied input VIN and some fraction of the output, while being insensitive to common-mode levels. In the case of a voltage follower, of course, the distinction between the signal and the common-mode voltage is somewhat fuzzy; the real value of the high common-mode rejection ratio (CMRR) afforded by OPAs is much more apparent when the amplifier is connected in a high-gain mode, and a small input signal is accompanied by an interfering common-mode signal.
Formally, this input cell is a nonlinear transconductance, whose output currents IC1 and IC2 are applied to the npn current-mirror Q3, Q4, which generates the difference IC1 - IC2. This current is then integrated by the 'HF compensation' capacitor, CC, in the main voltage-gain stage provided by the common-emitter stage Q5, which is forced to operate at a constant collector current of IT. The resulting output voltage is buffered by what is here shown as an ideal voltage-controlled voltage-source (VCVS) but which in most cases will be the familiar Class-AB complementary emitter-follower that provides the high current-gain to drive the load, RL.
In a real OPA, some of the open-loop distortion will arise in this VCVS stage, but in order to keep our sights focused on the main distortion mechanism, we can ignore that here. Notice that CC is connected to the final output node, not to the collector of Q5, as is often the case. This minor modification means that back-and-forth flow of the HF displacement current in CC is not supported by Q5 but, rather, by the output stage. Consequently, there is no variation in IC5 (it's held steady at IT) and thus the VBE of Q5 is likewise constant with output voltage.
All this groundwork may seem very tedious, but it is with a view to getting at the root cause of distortion. Numerous such detailed considerations are crucial to the design of an op amp capable of ultra-linear HF performance, and each needs to be eliminated independently. We're only considering the first of many, here.
Now we're ready to start the sums. Unfortunately, there is no painless way to avoid mathematics, but what we can do is use simple, even rudimentary, models for the transistors, in the spirit of Foundation Design. This approach to the quest for insight was mentioned in the "Spicing Up The Op Amp", and it's time to be a little more specific about this notion. It works very well for the bipolar junction transistor (BJT), which will probably remain a major technology -- certainly in the high-performance arena -- for at least the next decade, and beyond, in spite of the impressive advances in analog CMOS design, only made more difficult by the almost total emphasis on digital applications in the on-going development of sub-micron technologies. (Some of the reasons for holding to this view were stated in "Why Bipolar?".)
The Level-0 model for the BJT is simply a voltage-controlled current-source (VCCS) having an exact exponential relationship between its collector current, IC, and its base-emitter voltage, VBE; this is the heart of the BJT:
IC = IS exp (VBE/VT) (1)
where IS is the saturation current (and, only slightly whimsically, can be regarded as the BJT's soul, since it mediates so much of the device's personality) having a value of some 3.6E-18 amps for a VBE of 800 mV at IC = 100 mA and temperature of 27ıC. It's amazing to me, after having stared at this equation for the better part of my life, how very profound it is, traceable to fundamental aspects of carrier statistics in semiconductor materials. It is the well-spring of BJT magic. It takes but a moment to find that the transconductance dIC/dVBE of a single device is:
gm = IC/VT (2)
where VT is, of course, the thermal voltage kT/q, 26 mV at 30ıC. This remains as true for a modern complex SiGe heterojunction transistor as it was for the primitive junction-alloy devices that came along quite shortly after Bardeen, Brattain and Shockley went whooping up and down the halls of Bell Labs jubilantly shouting Eureka! It's fair to say that (1) and (2) are the most remarkable of all equations in modern electronics.
The Level-0 model also conveniently omits such pesky set-backs as the finite base current and Early voltage of a BJT, its ohmic resistances and parasitic capacitances, base transit time and other effects. Accordingly, we set BF = BR = VAF = VAR = 1E6, and most other parameters to zero. Crazy? Not really: This is just what first-order textbook analyses do, without drawing attention to the fact. It is nonetheless surprising just how much of the reality of an IC's behavior emerges from the application of this simple translinear model to circuit analysis. For example, the minimum permissible supply voltage will usually be correctly modeled; the shot noise will be right on the money; most of the temperature behavior; and, for the present purposes, an important distortion mechanism in OPAs will be quite accurately predicted.
to find it. Making it a thread here so that it is not lost forever. I believe that there was also a .pdf of it. Most of the
theory also applies to power amps.
There are a few Figures that were not captured.
A few very old links where it was discussed:
This one is almost 20 years old:
https://www.diyaudio.com/community/...rning-cordell-otala-and-gilbert-papers.48873/
Fairly certain that it was referenced here also, not saying that this is a good thread but here it is:
https://www.diyaudio.com/community/threads/whats-your-reasoning-and-not-whats-your-belief.41770/
Everyone knows that op amps are the most linear building blocks in the analog repertoire. If you want nonlinear behavior, you had better look to multipliers or other arcania. But we recognize that every real amplifier has a bit of nonlinearity, like it or lump it, so maybe we ought to take a look at just how good is that standard op amp, the voltage-mode amplifier identified as an 'OPA' in previous columns, when used at frequencies above a few Hertz.
It wasn't so many years ago, in the heyday of the uA741, that a guy called Otala discovered this early 1-MHz OPA performed a lot worse than might expected at audio frequencies, so he wrote a paper in the Journal of the Audio Engineering Society in which he coined a brand new term -- transient intermodulation distortion, or 'TIM' -- to describe in audio lingo what most users of op amps had already discovered, namely, the little matter of a limited slew-rate. It was a phenomenon peculiar to IC op amps. If you had grown up with vacuum tubes, you had plenty of reason to raise your eyebrows, since, unlike bipolar transistors (with their extremely high gm and a correspondingly small range over which linearity prevails in the familiar differential-pair gain cell), tube amplifiers rarely, if ever, got themselves into this pathological state of affairs.
Predictably, Otala's 'discovery' only added welcome fuel to the fire of those who were quite convinced that these new-fangled transistor amplifiers were genetically incapable of pleasing the audiophile ear, a notion which, like all myths, persists unabated, in spite of the fact that the root cause of TIM is now completely understood, and can easily be avoided in transistor amplifiers expressly designed for the most demanding audio applications. Nevertheless, Mister Otala was on to something, and although there are many splendid op amps out there, not all deliver quite what the textbooks promise. Accordingly, for a few minutes, we will examine a major source of distortion in op amps. Writing this in Kailua-Kona, Hawaii, with the thunder of the surf just feet away from this lanai, as the palms and hibiscus breathe the balmy post-dawn air, I have ample time on my hands.
The dominant mantra intoned over the application of op amps goes something like this: Never mind what's inside that cute little triangle; the function of the overall linear block -- invariably just a simple amplifier or filter stage -- is determined (almost entirely) by the passive components that are added to provide feedback. The triangle thing is merely the power-house that, come rain or shine, makes everything work out right in the end, by a kind of op-amp magic. The parenthetical inclusion is a concession to those who know a bit better, and it's the focus of this piece.
Reduced to essentials, most voltage-mode op amps, OPAs, are based on a topology like that shown in Fig. 1. To develop the theory, our device is here connected as a simple amplifier with a closed-loop gain of G, determined by the ratio (R1+R2)/R2, which can alternatively be expressed in terms of the feedback fraction b = 1/G. Because the dominant source of nonlinearity is in the input cell, the distortion will be lowest in the voltage-follower mode.
In the interests of clarity and analytical simplicity, we will assume here that the output is a perfect sinusoid, having an amplitude E and angular frequency w, that is, Esinwt, and work backwards from this output to deduce what VIN would need to be to generate that output. This may seem an odd approach, and it's certainly not essential to do it this way. However, many analyses involving the exponential behavior of transistors lead to transcendental solutions when pursued in the forward direction, and that's true in this case. A reverse-direction analysis quickly generates the key insights, and points towards the required modifications to effect a solution, at the price of a slight but not serious loss of rigor.
A bipolar implementation is shown, since many monolithic OPAs use this technology. A basic differential-pair Q1, Q2, also cast in pnp form, and having a near-perfect current-source IT in its 'tail', senses the difference between the applied input VIN and some fraction of the output, while being insensitive to common-mode levels. In the case of a voltage follower, of course, the distinction between the signal and the common-mode voltage is somewhat fuzzy; the real value of the high common-mode rejection ratio (CMRR) afforded by OPAs is much more apparent when the amplifier is connected in a high-gain mode, and a small input signal is accompanied by an interfering common-mode signal.
Formally, this input cell is a nonlinear transconductance, whose output currents IC1 and IC2 are applied to the npn current-mirror Q3, Q4, which generates the difference IC1 - IC2. This current is then integrated by the 'HF compensation' capacitor, CC, in the main voltage-gain stage provided by the common-emitter stage Q5, which is forced to operate at a constant collector current of IT. The resulting output voltage is buffered by what is here shown as an ideal voltage-controlled voltage-source (VCVS) but which in most cases will be the familiar Class-AB complementary emitter-follower that provides the high current-gain to drive the load, RL.
In a real OPA, some of the open-loop distortion will arise in this VCVS stage, but in order to keep our sights focused on the main distortion mechanism, we can ignore that here. Notice that CC is connected to the final output node, not to the collector of Q5, as is often the case. This minor modification means that back-and-forth flow of the HF displacement current in CC is not supported by Q5 but, rather, by the output stage. Consequently, there is no variation in IC5 (it's held steady at IT) and thus the VBE of Q5 is likewise constant with output voltage.
All this groundwork may seem very tedious, but it is with a view to getting at the root cause of distortion. Numerous such detailed considerations are crucial to the design of an op amp capable of ultra-linear HF performance, and each needs to be eliminated independently. We're only considering the first of many, here.
Now we're ready to start the sums. Unfortunately, there is no painless way to avoid mathematics, but what we can do is use simple, even rudimentary, models for the transistors, in the spirit of Foundation Design. This approach to the quest for insight was mentioned in the "Spicing Up The Op Amp", and it's time to be a little more specific about this notion. It works very well for the bipolar junction transistor (BJT), which will probably remain a major technology -- certainly in the high-performance arena -- for at least the next decade, and beyond, in spite of the impressive advances in analog CMOS design, only made more difficult by the almost total emphasis on digital applications in the on-going development of sub-micron technologies. (Some of the reasons for holding to this view were stated in "Why Bipolar?".)
The Level-0 model for the BJT is simply a voltage-controlled current-source (VCCS) having an exact exponential relationship between its collector current, IC, and its base-emitter voltage, VBE; this is the heart of the BJT:
IC = IS exp (VBE/VT) (1)
where IS is the saturation current (and, only slightly whimsically, can be regarded as the BJT's soul, since it mediates so much of the device's personality) having a value of some 3.6E-18 amps for a VBE of 800 mV at IC = 100 mA and temperature of 27ıC. It's amazing to me, after having stared at this equation for the better part of my life, how very profound it is, traceable to fundamental aspects of carrier statistics in semiconductor materials. It is the well-spring of BJT magic. It takes but a moment to find that the transconductance dIC/dVBE of a single device is:
gm = IC/VT (2)
where VT is, of course, the thermal voltage kT/q, 26 mV at 30ıC. This remains as true for a modern complex SiGe heterojunction transistor as it was for the primitive junction-alloy devices that came along quite shortly after Bardeen, Brattain and Shockley went whooping up and down the halls of Bell Labs jubilantly shouting Eureka! It's fair to say that (1) and (2) are the most remarkable of all equations in modern electronics.
The Level-0 model also conveniently omits such pesky set-backs as the finite base current and Early voltage of a BJT, its ohmic resistances and parasitic capacitances, base transit time and other effects. Accordingly, we set BF = BR = VAF = VAR = 1E6, and most other parameters to zero. Crazy? Not really: This is just what first-order textbook analyses do, without drawing attention to the fact. It is nonetheless surprising just how much of the reality of an IC's behavior emerges from the application of this simple translinear model to circuit analysis. For example, the minimum permissible supply voltage will usually be correctly modeled; the shot noise will be right on the money; most of the temperature behavior; and, for the present purposes, an important distortion mechanism in OPAs will be quite accurately predicted.
Audio Research LS1 what are those FETs?
- By gamerpaddy
- Tubes / Valves
- 4 Replies
ive got a Audio Research LS1 that has some hissing on the right channel that goes away once its running for a while, i suspect one of the old fet's going bad.
unfourtainly they are painted over and just marked FET, White Orange in the SM
Does anyone know what model they are?
Also whats going on here? are they just using them as capacitors?
i may also get a new 6922 tube to see if its the problem
unfourtainly they are painted over and just marked FET, White Orange in the SM
Does anyone know what model they are?
Also whats going on here? are they just using them as capacitors?
i may also get a new 6922 tube to see if its the problem
What makes a speaker driver expensive?
- Multi-Way
- 233 Replies
There is a huge difference in the price of loudspeakers. Some are a few dollars others are thousands. What are the factors that make a speaker driver expensive? If it was low distortion wouldn’t the distortion figures be advertised? Some is of course proprietary materials and expensive processes like MAOP or diamond coatings where the process often destroys more membranes and diaphrams than are used. There is also market demand, which I don’t think is a big deal for most hi-fi speakers. In the example below one is a matched pair, obviously there is a cost to match drivers to some tolerance, but is it worth $800?
What is the cost driver to produce good power handling, flat frequency response, low distortion, etc?
Here’s a somewhat absurd example from PE:
The least expensive full sized dome tweeter.
$6.98, GRS 1TD1-8 1" Dome Tweeter 8 Ohm ($13.96 for an unmatched pair)
A similar, and the most expensive, dome tweeter.
$808/pair, Morel TSCT1044 Supreme 1" Silk Dome Neodymium Tweeters - Matched Pair
What is the cost driver to produce good power handling, flat frequency response, low distortion, etc?
Here’s a somewhat absurd example from PE:
The least expensive full sized dome tweeter.
$6.98, GRS 1TD1-8 1" Dome Tweeter 8 Ohm ($13.96 for an unmatched pair)
A similar, and the most expensive, dome tweeter.
$808/pair, Morel TSCT1044 Supreme 1" Silk Dome Neodymium Tweeters - Matched Pair
Syn-11… a one-horn 5-way
About 2-3 weeks ago I got inspired by ncbluetj's BASH build which uses 4-15" !! https://www.diyaudio.com/community/threads/the-b-a-s-h.391536/page-6#post-7190481
Decided to see if I could retrofit a pair of 18" to an old synergy prototype....looked like it could work, providing a box could be built to wrap it.
The old proto is a 75x60 build that uses two 12"s, four 4"s, and a coax CD.
I'm like yeah, I can build a box around it, but it's going to be one heavy sucker. I'll need to build it on site, in its final resting place.
Decided I wanted to build it on a stand to match the height of other synergies sitting on tall subs. Used a vented sub box emptied and turned point up for the base.....(which already had coaster wheels, yay)
Built the box pieces and painted them. Time to assemble.
First thing was to mount the 12"s and seal them up the way the proto was designed.
So I can start putting it together on the stand.
Ann then add the rest of the drivers.
And then add the box.
Finish the wiring and seal her up...
Done. Assembly went nicely....took about 4 hours yesterday......happy camper 🙂
Decided to see if I could retrofit a pair of 18" to an old synergy prototype....looked like it could work, providing a box could be built to wrap it.
The old proto is a 75x60 build that uses two 12"s, four 4"s, and a coax CD.
I'm like yeah, I can build a box around it, but it's going to be one heavy sucker. I'll need to build it on site, in its final resting place.
Decided I wanted to build it on a stand to match the height of other synergies sitting on tall subs. Used a vented sub box emptied and turned point up for the base.....(which already had coaster wheels, yay)
Built the box pieces and painted them. Time to assemble.
First thing was to mount the 12"s and seal them up the way the proto was designed.
So I can start putting it together on the stand.
Ann then add the rest of the drivers.
And then add the box.
Finish the wiring and seal her up...
Done. Assembly went nicely....took about 4 hours yesterday......happy camper 🙂
Double Bass Array
- By 63781
- Subwoofers
- 60 Replies
I believe this forum doesn't have a thread dedicated to Double Bass Array (DBA), so I'm creating one.
Wikipedia article about DBA :
https://en.wikipedia.org/wiki/Double_bass_array
(Images below are taken from the Wiki article)
To create a DBA we must set up an array of at least four loudspeakers on the front wall, and a similar one on the rear wall. The rear array must play in reverse phase to actively absorb the plane wave from the front wall.
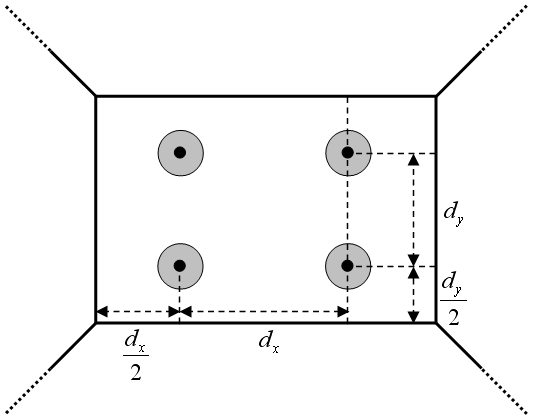
A simple way to understand what a DBA does can be described like this:
- The front array creates a plane wave which should cancel standing waves in the height- and width plane of the room (up to a certain frequency)
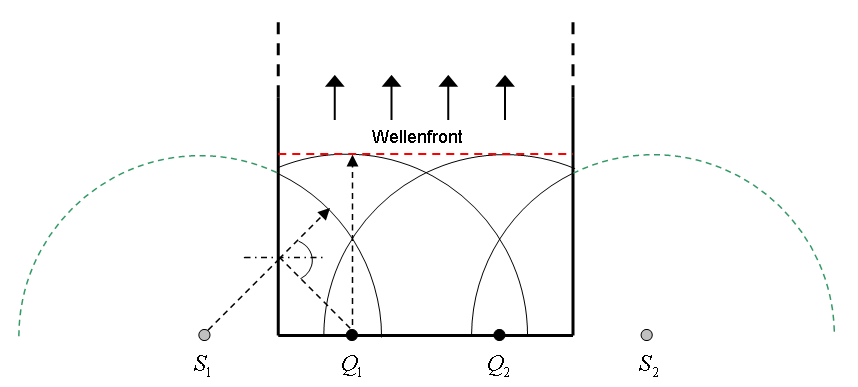
- The rear array shall actively absorb standing waves in the longitudinal plane
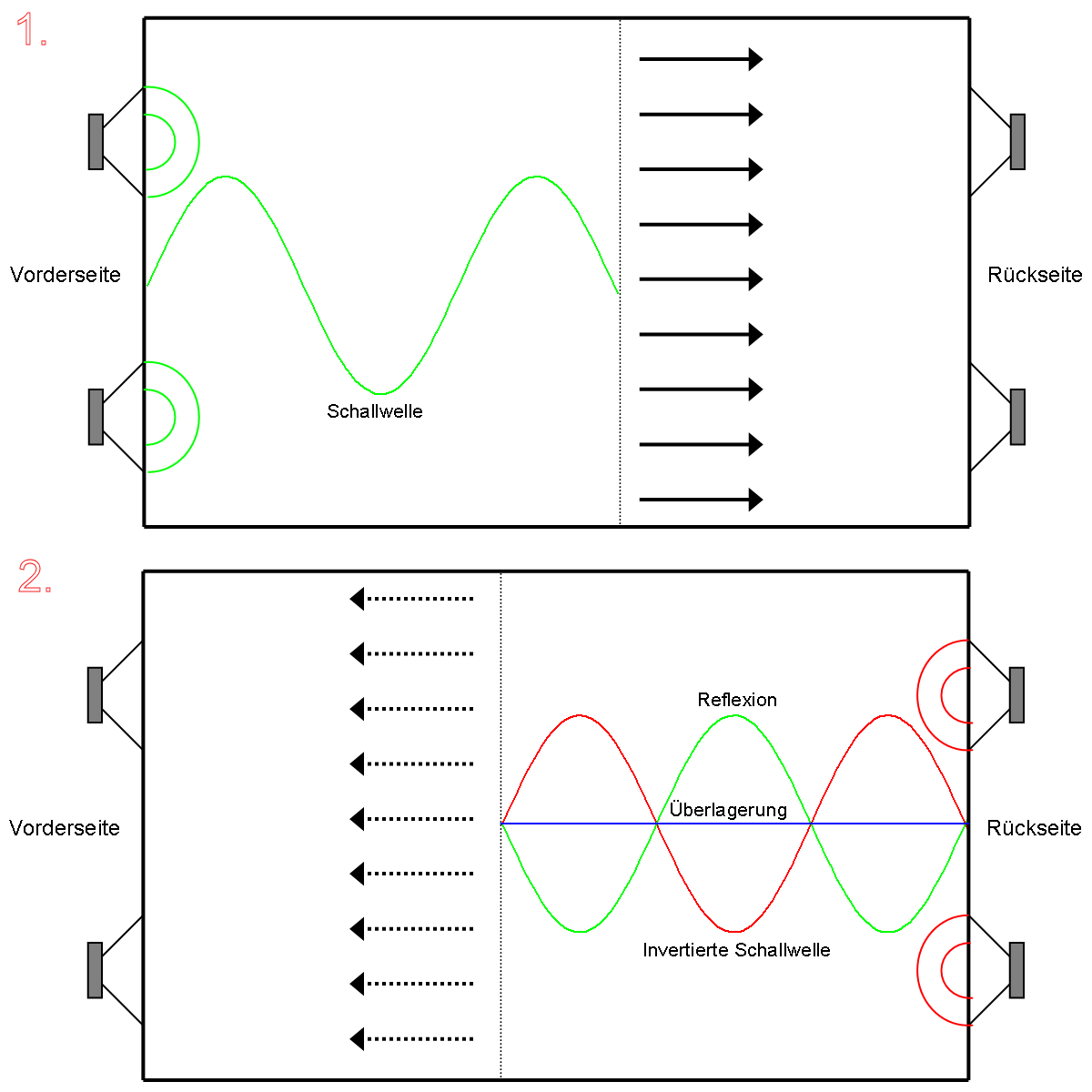
The result of this is that no standing waves should be exited, and you get a frequency response that is completely flat, and a decay without resonances. In theory at least. With some tweaking, it's possible in practice as well.
There are requirements and limitations of course:
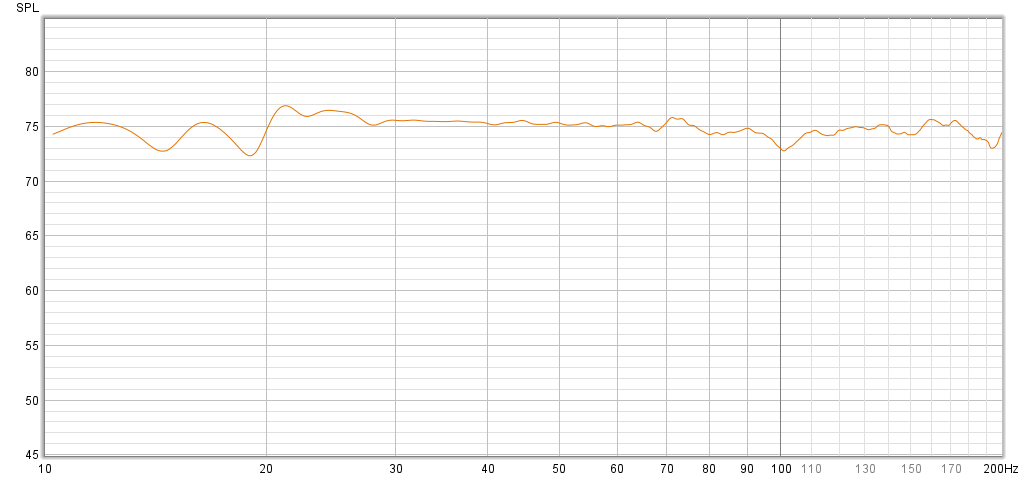
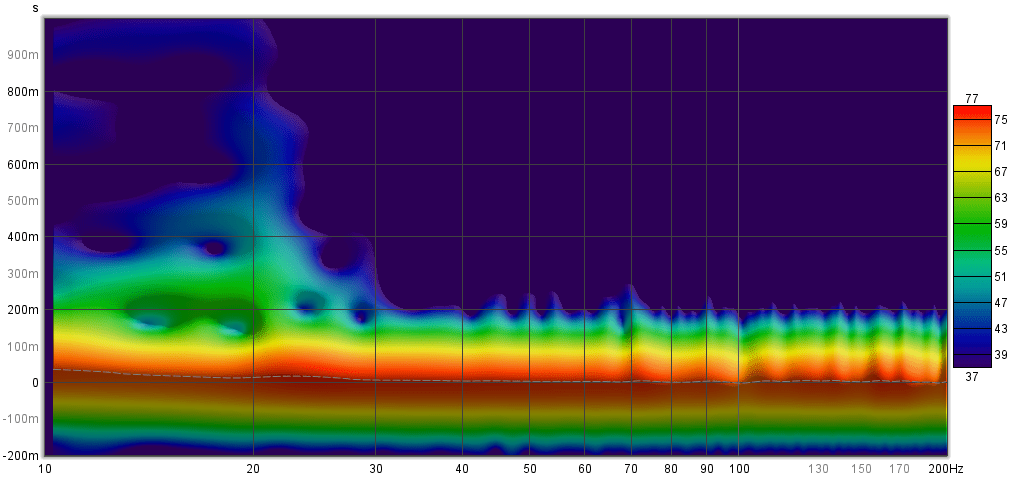
My own room doesn't meet any of these requirements. Even so, I was able to create this result with a lot of tweaking. The decay is very short down to about 30 Hz, where the neighboring room starts to contribute to the decay we see on the measurements here.
Wikipedia article about DBA :
https://en.wikipedia.org/wiki/Double_bass_array
(Images below are taken from the Wiki article)
To create a DBA we must set up an array of at least four loudspeakers on the front wall, and a similar one on the rear wall. The rear array must play in reverse phase to actively absorb the plane wave from the front wall.
A simple way to understand what a DBA does can be described like this:
- The front array creates a plane wave which should cancel standing waves in the height- and width plane of the room (up to a certain frequency)
- The rear array shall actively absorb standing waves in the longitudinal plane
The result of this is that no standing waves should be exited, and you get a frequency response that is completely flat, and a decay without resonances. In theory at least. With some tweaking, it's possible in practice as well.
There are requirements and limitations of course:
- The room should be rectangular with a flat ceiling (relatively easy to accomplish)
- The room should have very stiff surfaces. Concrete is good. Japanese paper walls are not.
- Apart from the loudspeaker arrays, the room should ideally be empty. Any objects disturbing the wave fronts will alter the result.
- Digital delay and EQ is required
- Measurements during setup is required
My own room doesn't meet any of these requirements. Even so, I was able to create this result with a lot of tweaking. The decay is very short down to about 30 Hz, where the neighboring room starts to contribute to the decay we see on the measurements here.
Matching SITs
It's known how to match FETs due to generosity of The One and Only. By the luck I've got some SITs and would of liked have them matched within reason. I can't make or borrow full blown curve tracer but I can plot a curve or two per device. What should I look for?|
PecanPi® DAC / Streamer Rev 3.0
- By orchardaudio
- Vendor's Bazaar
- 3 Replies
I am proud to announce the release of Rev 3.0 of my award winning PecanPi® product line.
.
The PecanPi Streamer is a networked music player with build-in DAC and headphone amplifier.
The PecanPi DAC is high-performance DAC for the RaspberryPi and Tinker Board, this is for DIYer and tinkers.
With Rev 3.0 the big change is the availability of an S/PDIF input.
The S/PDIF input has an automatic switch over that takes audio from the S/PDIF connection when there is a valid signal. When no valid signal is available on the S/PDIF interface the device defaults back to taking streaming data.
With Rev 3.0 the linear regulator have also been upgraded to use lower noise parts.
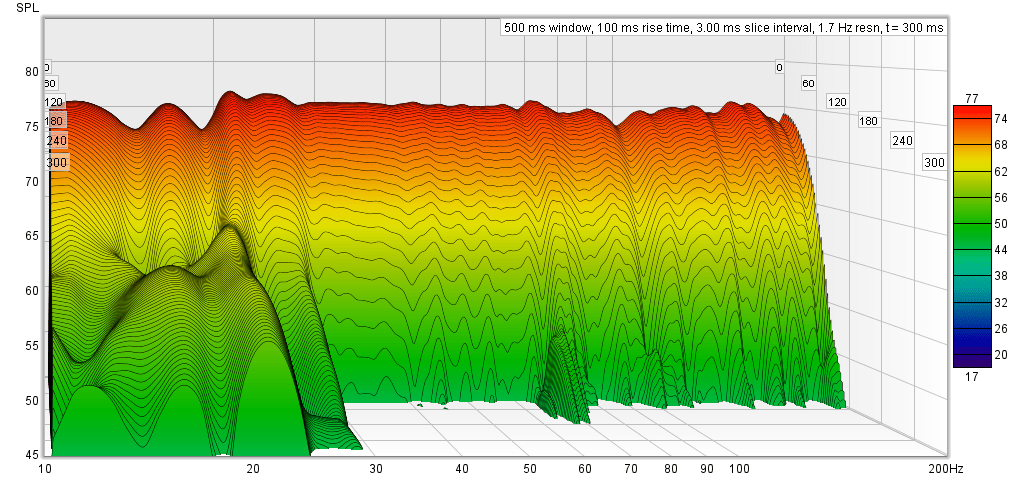
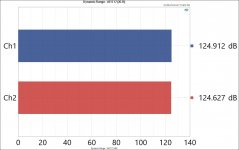
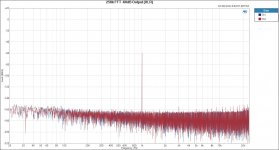
The audio performance remains the same as with previous versions. Below I retook some of the measurements using S/PDIF input.
Additional Details can be found on my website here:
www.orchardaudio.com
.The PecanPi Streamer is a networked music player with build-in DAC and headphone amplifier.
The PecanPi DAC is high-performance DAC for the RaspberryPi and Tinker Board, this is for DIYer and tinkers.
With Rev 3.0 the big change is the availability of an S/PDIF input.
The S/PDIF input has an automatic switch over that takes audio from the S/PDIF connection when there is a valid signal. When no valid signal is available on the S/PDIF interface the device defaults back to taking streaming data.
With Rev 3.0 the linear regulator have also been upgraded to use lower noise parts.
The audio performance remains the same as with previous versions. Below I retook some of the measurements using S/PDIF input.
Additional Details can be found on my website here:
www.orchardaudio.com
My New Cassette Deck
- Analogue Source
- 2 Replies
I'd had this Sharp cassette deck for fifty-two years, it's always played well, I put this video of it on YouTube.
Login to view embedded media
But lately I'd noticed a bit of noise from the left-hand channel when I turn it on. I hardly ever play it, but It's "there" if I want to. I like all my stuff to be working. But it's not worth having it repaired.
But I had a stroke of luck, I found this listed on eBay. Now for me, the "deal breaker," was the connections. It used din plugs on the lead like the other, I wouldn't have considered it if it didn't. The vendor said it was working, but hadn't tested it. That always throws up "red flags," but I decided if I bought it and it didn't work, it would be going back.
It's a Sharp RT-2500 Full auto-stop, auto Cr O2 plus Dolby.
What really impressed me was the condition in the vendor's photos. Not a mark on the cabinet, but although the black plastic had faded with age a bit, the lettering on the "POWER" and "EJECT" buttons were still clearly visible. If the lettering had worn, it would suggest to me a lot of use.
Anyway, I put in a bid and won. It arrived, extremely well packed. I checked it out and there was a lot of distortion on one channel. But a good clean of the heads with switch cleaner on a cotton bud cleared that problem.
The fast forward/return "didn't." It's usually a stretched belt. I had a spare set for the 442 which had a similar mechanism, so another fault cured.
Then gave the rest a good clean and it was good to go.
All the lights work.
It's only "mid range" but will do for me.
Well worth the £38 I paid for it. Which was half what I paid for the 442 in 1972.
Sounds OK.
Login to view embedded media
"Little Susanna Hoffs," the Bangles lead singer, was 65 earlier this year.
Doesn't time fly?
Login to view embedded media
But lately I'd noticed a bit of noise from the left-hand channel when I turn it on. I hardly ever play it, but It's "there" if I want to. I like all my stuff to be working. But it's not worth having it repaired.
But I had a stroke of luck, I found this listed on eBay. Now for me, the "deal breaker," was the connections. It used din plugs on the lead like the other, I wouldn't have considered it if it didn't. The vendor said it was working, but hadn't tested it. That always throws up "red flags," but I decided if I bought it and it didn't work, it would be going back.
It's a Sharp RT-2500 Full auto-stop, auto Cr O2 plus Dolby.
What really impressed me was the condition in the vendor's photos. Not a mark on the cabinet, but although the black plastic had faded with age a bit, the lettering on the "POWER" and "EJECT" buttons were still clearly visible. If the lettering had worn, it would suggest to me a lot of use.
Anyway, I put in a bid and won. It arrived, extremely well packed. I checked it out and there was a lot of distortion on one channel. But a good clean of the heads with switch cleaner on a cotton bud cleared that problem.
The fast forward/return "didn't." It's usually a stretched belt. I had a spare set for the 442 which had a similar mechanism, so another fault cured.
Then gave the rest a good clean and it was good to go.
All the lights work.
It's only "mid range" but will do for me.
Well worth the £38 I paid for it. Which was half what I paid for the 442 in 1972.
Sounds OK.
Login to view embedded media
"Little Susanna Hoffs," the Bangles lead singer, was 65 earlier this year.
Doesn't time fly?
The Aperdioid - ish
- By vdljev
- Full Range
- 10 Replies
Hi there, i was inspired by Nola brios since i have two TG9 4 ohm, and i came out with this.
With my limited understanding, it seems the phase shift an aperiodic TL provides helps create a cancelation over a wide band.
In this case, the TL is tuned so there is a 360° phase difference at approx 650 Hz, and below that, until port tuning freq (200 Hz), i get a nice rear wave cancelation. This was choosed as an 3.5 inch driver is expected to abandom omni pattern arround there. For some reason, the OB makes for a better cancelation (in vituixcad), if its inverted, as prob brios are, according to some measurments in the brio thread.
Vituixcad shows awesome cancelation, but little arround TL tuning f, AKABAK shows the opposite.
Some sim images to show what i'm talking about...
The akabak sim is for generic speaker, no LEM data inserted as of now. TL was simed using Leonard audio and then translated to the other programs.
Now that both programs are showing the effect i'm after, i'll make some more iterations on akabak, and i'm gonna build it soon-
recomendations welcomed! Best regards!
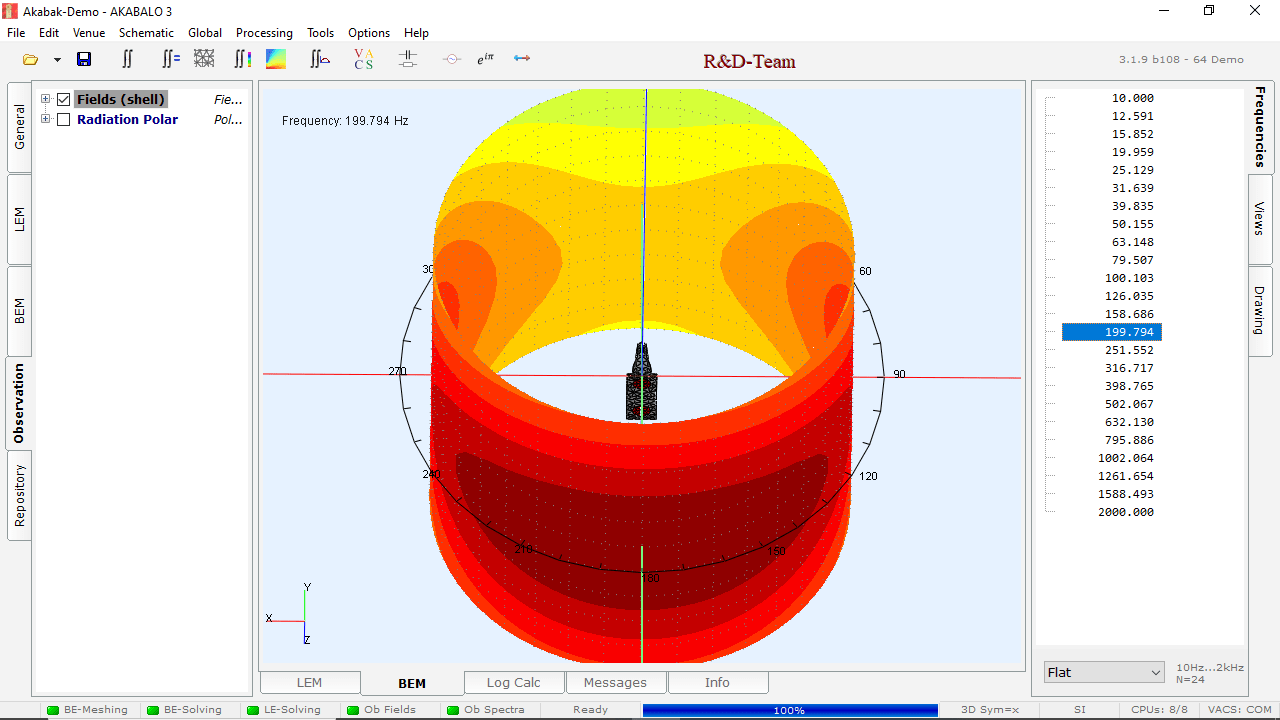
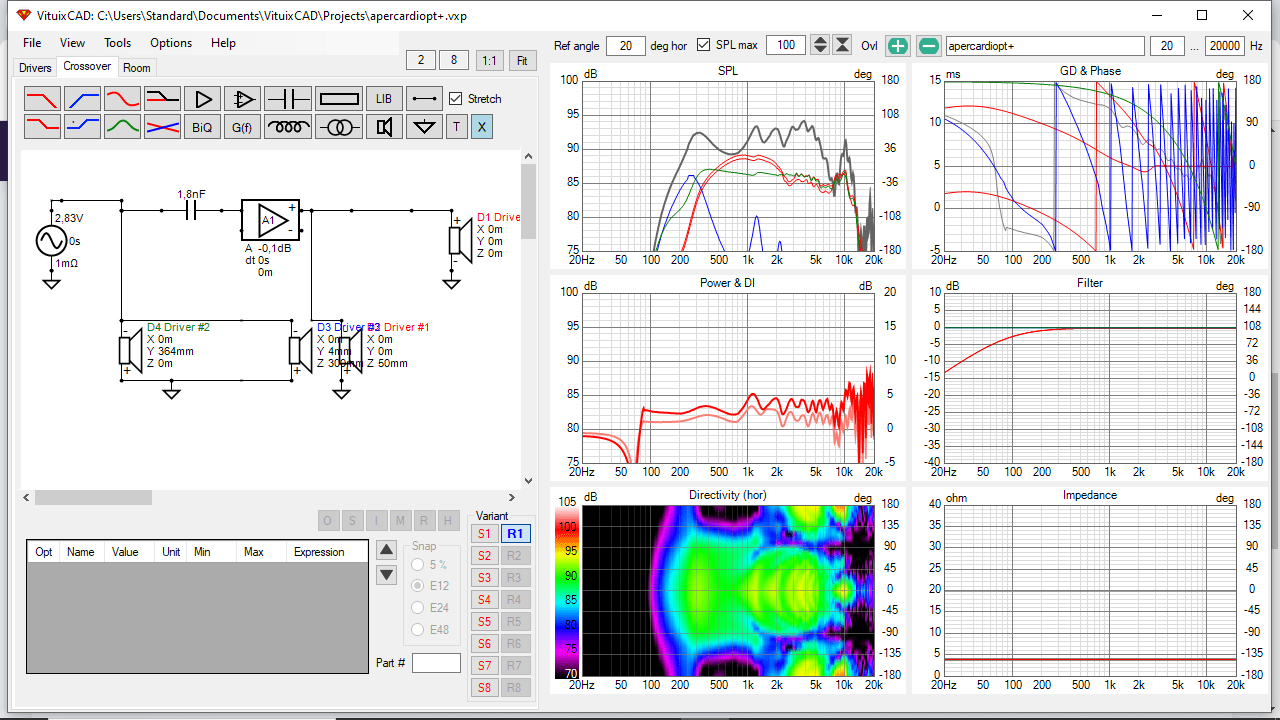
This one is an imposible thing, as port distance from front baffle is about double of the TL, but it shows the effect real nice. I also ended up making distance between drivers 220 mm as 364 mm seemed like too much visually. Also, it makes the dip at 8Khz way more benign. The idea is that some day far from now, some supertweeter will lay there.
(forget the cap its not doing anything) (i will waste some power to make the load 4 ohm)
I bet this speakers from project10 are pretty directional too: https://www.diyaudio.com/community/threads/aperiodic-loading-to-lower-qt.162130/
With my limited understanding, it seems the phase shift an aperiodic TL provides helps create a cancelation over a wide band.
In this case, the TL is tuned so there is a 360° phase difference at approx 650 Hz, and below that, until port tuning freq (200 Hz), i get a nice rear wave cancelation. This was choosed as an 3.5 inch driver is expected to abandom omni pattern arround there. For some reason, the OB makes for a better cancelation (in vituixcad), if its inverted, as prob brios are, according to some measurments in the brio thread.
Vituixcad shows awesome cancelation, but little arround TL tuning f, AKABAK shows the opposite.
Some sim images to show what i'm talking about...
The akabak sim is for generic speaker, no LEM data inserted as of now. TL was simed using Leonard audio and then translated to the other programs.
Now that both programs are showing the effect i'm after, i'll make some more iterations on akabak, and i'm gonna build it soon-
recomendations welcomed! Best regards!
This one is an imposible thing, as port distance from front baffle is about double of the TL, but it shows the effect real nice. I also ended up making distance between drivers 220 mm as 364 mm seemed like too much visually. Also, it makes the dip at 8Khz way more benign. The idea is that some day far from now, some supertweeter will lay there.
(forget the cap its not doing anything) (i will waste some power to make the load 4 ohm)
I bet this speakers from project10 are pretty directional too: https://www.diyaudio.com/community/threads/aperiodic-loading-to-lower-qt.162130/
Can you identify this DIY tube amp PCB?
- By Cornwallav8r
- Tubes / Valves
- 4 Replies
I've got this unknown amp new PCB, it indicates 6BM8 tubes in the small text. Text reads: Experimenter's 6BM8 Push Pull Stereo Amplifier...Richard Sears Rev 051810. Does anybody know this board or have a schematic for it? Seems a waste to throw it away.
![20240708_094034[1].jpg](https://www.diyaudio.com/community/attachments/20240708_094034-1-jpg.1331421/ "20240708_094034[1].jpg")
Hello there
- By Max12
- Introductions
- 1 Replies
Hey there, just joined the forum, currently planing on building myself some SyntripPs to go with my lonely TH12 tapped subwoofers
Greetings Maxi
Greetings Maxi
Help! AliExpress Crossover Values on Cerwin Vega E312
Hey, hoping for some observations on these crossovers I picked up for a little Cerwin Vega project I have planned with my brother. I have a set of Cerwin E-312 and the crossovers are really subpar.. So in thinking about stuff for the both of us to do as a project, I thought of redoing these speakers I have in my workshop.
Here is the crossover I picked:
https://www.aliexpress.com/item/1005005705670791.html
First off, I'd probably do some obvious things like remove the cheap screwed on terminals and solder wire direct. But in reading reviews, these Russian guys were all sounding off on incorrect values used on the LF portion - the 2.7uF specifically and how it should be larger. Having a look, trying to see what they are talking about, if anything at all. I'd also bypass a few caps too, maybe hard-wire the midrange jumper. Interested in some thoughts. Fortunately there was a pic posted of the backside of the PCB. What do you think of extras to do on these?
Here is the crossover I picked:
https://www.aliexpress.com/item/1005005705670791.html
First off, I'd probably do some obvious things like remove the cheap screwed on terminals and solder wire direct. But in reading reviews, these Russian guys were all sounding off on incorrect values used on the LF portion - the 2.7uF specifically and how it should be larger. Having a look, trying to see what they are talking about, if anything at all. I'd also bypass a few caps too, maybe hard-wire the midrange jumper. Interested in some thoughts. Fortunately there was a pic posted of the backside of the PCB. What do you think of extras to do on these?
Sub phase alignment
- By stajo
- Subwoofers
- 16 Replies
Hi, I didnt know if I should ask here or at Multi Way but you dudes that are into subs might know. So I have done some repositioning of speakers and listening position etc and listening and measuring, trying to understand what happens. I have come up with a placement that suits me fairly for my LP and the speakers. It sounds ok, still doing tweaking with speaker stuffing (its TQWT) that changes things quite alot. Lately I have also added two subs that are placed ca 1,5 m in front of the speakers. I assumed that I will have to run those thru a dsp because of likely phase disalignment with the speakers woofers. But It doesnt sound or measure as I will have to.
The system is analog but actively crossed at 1000 hz, and I feed the subs with an extra buffer that I have tapped from the LF outputs on the active x-over, so they have a 20-1000 hz signal. The main speakers has a fairly good respons down to abt 40, than they fall pretty steep. So I turned the local low pass button on the subs all anticlockwise to lowest lowpass fq, hoping that they will cut over 40 or so. And maybe they do but not very steep, as seen in measures.
But, now to my main poll. Do you agree that it doesnt look like I have a big problem with phase woofer/subs, so maybe I can skip the dsp and work with some sub eq instead?
Lower is speakers only, both channels, upper is with subs added.
The system is analog but actively crossed at 1000 hz, and I feed the subs with an extra buffer that I have tapped from the LF outputs on the active x-over, so they have a 20-1000 hz signal. The main speakers has a fairly good respons down to abt 40, than they fall pretty steep. So I turned the local low pass button on the subs all anticlockwise to lowest lowpass fq, hoping that they will cut over 40 or so. And maybe they do but not very steep, as seen in measures.
But, now to my main poll. Do you agree that it doesnt look like I have a big problem with phase woofer/subs, so maybe I can skip the dsp and work with some sub eq instead?
Lower is speakers only, both channels, upper is with subs added.
modifying valve amp with net/single bias trimpot
- By lordearl
- Tubes / Valves
- 35 Replies
I've recently switched out a set of EL34 tubes in the attached circuit and find adjusting the bias a rather painful process as the adjustment is done on a net basis for both tubes and it is very hard to get the tubes matched to an acceptable level.
What would be the most efficient way to add in a second trimpot so each power tube could be adjusted separately?
What would be the most efficient way to add in a second trimpot so each power tube could be adjusted separately?
Avalanche AS1 modernization
Avalanche AS1 was an active 3-way speaker made in early '90s in Finland by a small company in Eastern Finland.
It is an active 3-way speaker with analog line level xo and three amplifier boards with Hitachi K135 MOSFET amplifiers.The box is made of soupstone, dead weight 86kg a piece! Drivers are ScanSpeak 21W/8555 (pair) Audax/Polydax 4" mids (pair) and a Dynaudio D28 tweeter.
This pair was for sale at a Finnish hifi-forum, and to my surprise I knew the owner! He had bought this pair just before the bankcrupcy of the company. The speakers had one bass drivers changed but still they suffered from poor sound.
I just had to push the buy button, but for totally altruistic reasons - I will give this pair to my younger son!
It is an active 3-way speaker with analog line level xo and three amplifier boards with Hitachi K135 MOSFET amplifiers.The box is made of soupstone, dead weight 86kg a piece! Drivers are ScanSpeak 21W/8555 (pair) Audax/Polydax 4" mids (pair) and a Dynaudio D28 tweeter.
This pair was for sale at a Finnish hifi-forum, and to my surprise I knew the owner! He had bought this pair just before the bankcrupcy of the company. The speakers had one bass drivers changed but still they suffered from poor sound.
I just had to push the buy button, but for totally altruistic reasons - I will give this pair to my younger son!
Darling 1626 Amp
- By jcmusic
- Tubes / Valves
- 18 Replies
I picked up this little amp a few weeks ago and was just wondering if anyone here could offer advice on tubes to improve or change the sound?
Here are the details from the builder in 2010.
I built this little amp about 6 months ago and it's seen about 25 hours of use. You could think of the amp as a JE Labs "Simple 45" except it uses the 1626 output tube (the schematics are virtually identical except for output tubes and naturally different operating points).
The tubes include a 5U4GB rectifier, a pair of 1940's Hytron 1626 power tubes and an RCA JAN Black Plate (graphite coated envelope) 12SL7 driver tube (all tubes were new with the amp and have about 25 hours on them max).
I've really enjoyed this amp in my Den and used it to drive some custom made 94 DB single driver speakers with plenty of volume and dynamics for my listening level. The tube puts out about .75 watts per channel so more efficient speakers will be needed in a larger room. However, I let one of my friends with a pair of Lowther Alerion speakers at around 94 db efficiency listen to it in his larger room and he really liked it. But he already has two of my hand built amps and couldn't really justify buying another one (he has several other tube amps as well) so this one is available to the public at large.
The amp has an overbuilt power supply and is really quiet. I used a seperate filament transformer with center tap to help with hum balance and avoid any coupling noises between windings in the power transformer which I think helped.
Some other details about the amp:
-- NOS USA Made Pyramid Paper in Oil Coupling Capacitors
-- Teflon Jacketed Silver Clad copper for all signal carrying wires.
-- Made in USA new Edcor output transformers
-- Super short signal path, with an attempt to use only the leads on most resistors to minimize the number of solder joints.
-- Lead free Kester 3% silver solder used exclusively
-- Vintage Power transformer that I picked up on Ebay last Summer (spray painted it a hammertone black to match the plinth).
-- A hybrid star ground that uses a short silver clad copper bus bar that is reputed to be quieter than a straight star ground (high currents are kept from commingling with sensative signal circuits).
The amp is point to point wired, although I did build the power supply on a perf-board to conserve space and to better group the power supply grounding node.
Here are the details from the builder in 2010.
I built this little amp about 6 months ago and it's seen about 25 hours of use. You could think of the amp as a JE Labs "Simple 45" except it uses the 1626 output tube (the schematics are virtually identical except for output tubes and naturally different operating points).
The tubes include a 5U4GB rectifier, a pair of 1940's Hytron 1626 power tubes and an RCA JAN Black Plate (graphite coated envelope) 12SL7 driver tube (all tubes were new with the amp and have about 25 hours on them max).
I've really enjoyed this amp in my Den and used it to drive some custom made 94 DB single driver speakers with plenty of volume and dynamics for my listening level. The tube puts out about .75 watts per channel so more efficient speakers will be needed in a larger room. However, I let one of my friends with a pair of Lowther Alerion speakers at around 94 db efficiency listen to it in his larger room and he really liked it. But he already has two of my hand built amps and couldn't really justify buying another one (he has several other tube amps as well) so this one is available to the public at large.
The amp has an overbuilt power supply and is really quiet. I used a seperate filament transformer with center tap to help with hum balance and avoid any coupling noises between windings in the power transformer which I think helped.
Some other details about the amp:
-- NOS USA Made Pyramid Paper in Oil Coupling Capacitors
-- Teflon Jacketed Silver Clad copper for all signal carrying wires.
-- Made in USA new Edcor output transformers
-- Super short signal path, with an attempt to use only the leads on most resistors to minimize the number of solder joints.
-- Lead free Kester 3% silver solder used exclusively
-- Vintage Power transformer that I picked up on Ebay last Summer (spray painted it a hammertone black to match the plinth).
-- A hybrid star ground that uses a short silver clad copper bus bar that is reputed to be quieter than a straight star ground (high currents are kept from commingling with sensative signal circuits).
The amp is point to point wired, although I did build the power supply on a perf-board to conserve space and to better group the power supply grounding node.