Understand that, with the Gaussian (or any FIR) version of the crossover with 4th-order highpass section, one need not create the elaborate structure with dual delays, etc. One need only compute the lowpass impulse response once, save it as an FIR filter, and subtract the delayed full-bandwidth signal from the lowpass output to create the highpass filter.Berchin 8x4 Gaussian version, delay = 2x1381 samples. Gaussian impulse response for FIR filter attached below for anyone who is interested.
Actually, the same holds true for the Gaussian version with 2nd-order highpass section.
There is a simple multiway structure presented in the original AES paper. I haven't attempted to adapt that structure to the version of the crossover that has 4th-order highpass, so I don't know if it's possible. Otherwise a traditional branched structure could be used.How difficult would it be to implement a full 3 or 4 way crossover for given frequencies?
That would be my recommendation, if sufficient computational resources exist.Or would it make better sense to use this for the lowest band only and then FIR above?
Perhaps that is the nomenclature that we should adopt; "8x2" or "8x4" for 8th-order Bessel LPF with 2nd- or 4th-order derived HPF, respectively; "Gx2" or Gx4" for Gaussian; "4x2" or "4x4", etc. Much more compact, yet unambiguous. Thanks @newvirus2008.The Berchin 8x4 crossover
Note also that the original concept can be extended to higher-order highpass sections, but the complexity increases as does the length of the impulse response.
So, no cascading MDS required ? Maybe I didn't follow correctly. Could you rephrase that a little if you don't mind ?Understand that, with the Gaussian (or any FIR) version of the crossover with 4th-order highpass section, one need not create the elaborate structure with dual delays, etc. One need only compute the lowpass impulse response once, save it as an FIR filter, and subtract the delayed full-bandwidth signal from the lowpass output to create the highpass filter.
Actually, the same holds true for the Gaussian version with 2nd-order highpass section.
I think it was SubSoniks who first used that kind of suffix (here), I just picked that up since it was convenient. Mark100 used GB4th, GB8th etc.Perhaps that is the nomenclature that we should adopt; "8x2" or "8x4" for 8th-order Bessel LPF with 2nd- or 4th-order derived HPF, respectively; "Gx2" or Gx4" for Gaussian; "4x2" or "4x4", etc. Much more compact, yet unambiguous.
@pelanj, Please note that it's 511 samples, not 512. thanks.Here's a 1023-point Gaussian FIR for 100Hz if you want to try. I think the delay would then be 512 samples.
If one is creating a FIR implementation, then the structure that I showed in message #316 is not necessary for realtime operation. Instead, use the structure in #316 to compute the lowpass impulse response and use that impulse response as the FIR lowpass filter coefficients. Derive the highpass filter from the lowpass filter by delaying the full-bandwidth signal half the LPF length, and subtracting the LPF from it -- just as in the Gx2 case.So, no cascading MDS required ? Maybe I didn't follow correctly. Could you rephrase that a little if you don't mind ?
The only time that the full structure in #316 is necessary (other than for computing the impulse response, above) is when IIR filters are being used in realtime operation.
I hope that's understandable. If not, please ask again.
Thank you @SubSoniks.I think it was SubSoniks who first used that kind of suffix (here), I just picked that up since it was convenient.
Ok, I guess it's like pre-compute/pipeline the larger structure as an FIR fiter, and perform only the final MDS in real-time, correct ?I hope that's understandable. If not, please ask again.
Correct. All that you need is the overall impulse response.Ok, I guess it's like pre-compute/pipeline the larger structure as an FIR fiter, and perform only the final MDS in real-time, correct ?
@newvirus2008, have you found this to be true in general? As I mentioned, I haven't got around to formalizing the determination of correct delay, only having spot-checked a few cases for each filter order. If your discovery holds true in general, then I will modify my script to incorporate it. Thanks.my delay seems to happen at 337 samples, which is, once again, equivalent to the 7ms max delay of the Bessel.
Ok, here is the overall impulse response of the Gx8 low-pass filter. Rename the attached file to *.wav and use 1381-sample delay to obtain the subtractive high-pass filter.All that you need is the overall impulse response.
Also, @pelanj please note that this response cannot be faithfully represented using 1024 points.
Until now, I've found it to be true for all orders of the 100Hz filter that I've been trying, where the GD at DC and that at 100Hz match to within 1 sample-time. I think @SubSoniks also used the same delay as the GD of his filter (9.0ms).@newvirus2008, have you found this to be true in general? As I mentioned, I haven't got around to formalizing the determination of correct delay, only having spot-checked a few cases for each filter order. If your discovery holds true in general, then I will modify my script to incorporate it. Thanks.
However, to be on the safer side, I think it maybe better to use the group delay at the crossover frequency (vs. the max delay at DC), as the above-mentioned property may not hold for filters with higher group delays (lower cutoff frequencies than 100).
Of course, for FIR filters, the script could directly obtain the delay as N/2±1.
Attachments
Last edited:
For the classic subtractive-delay crossover it is definitley the case that the fullrange delay must be equal to the group-delay of the lowpass at 0 Hz and not equal at the crossover frequency. I guess this is also the case here.
Regards
Charles
Regards
Charles
I believe that's "Gx4"; Gaussian LPF with derived 4th-order HPF.Ok, here is the overall impulse response of the Gx8 low-pass filter.
Great; thank you. I'll use that as my starting point and see if any fine-tuning is necessary.Until now, I've found it to be true for all orders of the 100Hz filter that I've been trying, where the GD at DC and that at 100Hz match to within 1 sample-time.
Oh, yes Gx4, correct.
For a 25Hz (-6dB) 8th Bessel, 25Hz is GD-wise misaligned from 1Hz by only 1.77 samples at 48kHz. While it is highly unlikely that anyone would ever need a crossing lower than that, it is worth noting that the error is still too small to cause any big issues.
You may look at the higher order / higher sample-rate implementations for consistency though. Maybe Mark can help you with his observations on the 10th and 16th ones.
For a 25Hz (-6dB) 8th Bessel, 25Hz is GD-wise misaligned from 1Hz by only 1.77 samples at 48kHz. While it is highly unlikely that anyone would ever need a crossing lower than that, it is worth noting that the error is still too small to cause any big issues.
You may look at the higher order / higher sample-rate implementations for consistency though. Maybe Mark can help you with his observations on the 10th and 16th ones.
I also tried 10th order (about 20.8ms delay) and 16th order (about 26.7ms) ....Will post if anyone wants....
Last edited:
I have verified that "group delay at DC" provides the proper alignment delay for Bessel lowpass filters of orders 3-8. Tested at frequencies of 100Hz and 10,000Hz -- it's really sensitive at the higher frequencies, as one might expect.
EDIT: 48kHz sampling rate
EDIT: 48kHz sampling rate
At such low frequencies, one is dealing with tremendous group delay issues from the woofers anyway, so linear-phase filters probably won't make a lot of difference and traditional filters might be a reasonable choice.For a 25Hz (-6dB) 8th Bessel, 25Hz is GD-wise misaligned from 1Hz by only 1.77 samples at 48kHz. While it is highly unlikely that anyone would ever need a crossing lower than that, it is worth noting that the error is still too small to cause any big issues.
I've been adjusting for maximum HP attenuation whilst keeping an eye on the crossover point being -6dB down, I have tried to measure the GD at low frequencies but it is not so easy or stable with the equipment I have here. The 9ms was copied from your post #289Until now, I've found it to be true for all orders of the 100Hz filter that I've been trying, where the GD at DC and that at 100Hz match to within 1 sample-time. I think @SubSoniks also used the same delay as the GD of his filter (9.0ms).
I've not found a way to do this, I think it would be a useful addition, I have one request in the pipeline with them, they seem very open to suggestions.Oh, and with OSM, do you know how to delete all measurements at once? thx.
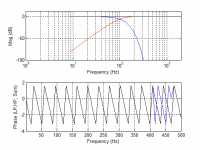
Re scaling, I worked out the scaling factor for 8th order Bessel from what you posted based on Greg's scaling factor to work directly from the Bessel tables and also worked out the scaling for the the 4th order by iteration, should be good to one decimal place.The Berchin 8x4 crossover also works as expected, but the crossing has risen from 100Hz to 129Hz, like @SubSoniks was having earlier. It now becomes obvious that scaling the LPF to 77Hz would bring the cutoff back to 100Hz, with an alignment delay of 9.0ms, as was seen in post #289.
Scaling factors I have are:
4th order Bessel: /1.76
8th order Bessel: /1.795
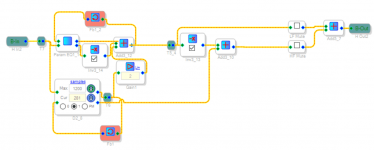
I have also had a play with your optimised version, I used a couple of feedback loops to reduce the amount of adjustment tabs.
I'm currently using an ADAU1466 DSP but a somewhat less powerful DSP such as the the ADAU1701 which is available for pennies will work fine with the Bessel derived GB filters.
I'm currently using an ADAU1466 DSP but a somewhat less powerful DSP such as the the ADAU1701 which is available for pennies will work fine with the Bessel derived GB filters.
Attachments
I suspect that the Bessel tables to which you refer generate Bessel filters that are -3 dB at your specified cutoff frequency, not -6 dB. Correct? I am so accustomed to using -6 dB Bessel filter equations that I forget I had to generate them myself.Re scaling, I worked out the scaling factor for 8th order Bessel from what you posted based on Greg's scaling factor to work directly from the Bessel tables and also worked out the scaling for the the 4th order by iteration, should be good to one decimal place.
Scaling factors I have are:
4th order Bessel: /1.76
8th order Bessel: /1.795
Here are the Bessel lowpass filter denominator polynomials that generate -6 dB at 1.0 rad/sec (I wish that the editor here would preserve tabs.):
1
s + 0.577350269189625
2
(Q = 0.57735) s² + 1.51748993932003s + 0.767591905312504
3
(Q = 0.69105) s² + 1.51690751998813s + 1.0988360782234
s + 0.957780847294575
4
(Q = 0.80554) s² + 1.45791596812417s + 1.37923209297774
(Q = 0.52193) s² + 2.00706006531024s + 1.0973694993458
5
(Q = 0.91648) s² + 1.39865560086264s + 1.64310407474472
(Q = 0.56354) s² + 2.01672663783782s + 1.29162610822856
s + 1.09704214355081
6
(Q = 1.02331) s² + 1.35027150823981s + 1.90923769367689
(Q = 0.61119) s² + 2.00491112629497s + 1.50158248373144
(Q = 0.51032) s² + 2.28004496305045s + 1.35384298459159
7
(Q = 1.12626) s² + 1.3126237600054s + 2.18552584665144
(Q = 0.66082) s² + 1.98927928173616s + 1.72806352056746
(Q = 0.53236) s² + 2.32561305242455s + 1.532776121137
s + 1.21497965956963
8
(Q = 1.22567) s² + 1.28299239215439s + 2.47283345436118
(Q = 0.71085) s² + 1.9741153642581s + 1.96926212166436
(Q = 0.55961) s² + 2.35216938769735s + 1.73263396575613
(Q = 0.50599) s² + 2.52527503176501s + 1.6326875194579
9
(Q = 1.32191) s² + 1.25882651612532s + 2.76908688019576
(Q = 0.76061) s² + 1.95987915089682s + 2.22220333341006
(Q = 0.58941) s² + 2.36803531877968s + 1.94807468608236
(Q = 0.51971) s² + 2.58984069125509s + 1.81161516486553
s + 1.33033917731169
10
(Q = 1.41531) s² + 1.2383906778965s + 3.07197590340822
(Q = 0.80977) s² + 1.9463531040995s + 2.48421464566909
(Q = 0.62047) s² + 2.37707641403698s + 2.17534467756742
(Q = 0.53755) s² + 2.63510305440823s + 2.00648730986839
(Q = 0.50391) s² + 2.75729393738485s + 1.9305310305774
1
s + 0.577350269189625
2
(Q = 0.57735) s² + 1.51748993932003s + 0.767591905312504
3
(Q = 0.69105) s² + 1.51690751998813s + 1.0988360782234
s + 0.957780847294575
4
(Q = 0.80554) s² + 1.45791596812417s + 1.37923209297774
(Q = 0.52193) s² + 2.00706006531024s + 1.0973694993458
5
(Q = 0.91648) s² + 1.39865560086264s + 1.64310407474472
(Q = 0.56354) s² + 2.01672663783782s + 1.29162610822856
s + 1.09704214355081
6
(Q = 1.02331) s² + 1.35027150823981s + 1.90923769367689
(Q = 0.61119) s² + 2.00491112629497s + 1.50158248373144
(Q = 0.51032) s² + 2.28004496305045s + 1.35384298459159
7
(Q = 1.12626) s² + 1.3126237600054s + 2.18552584665144
(Q = 0.66082) s² + 1.98927928173616s + 1.72806352056746
(Q = 0.53236) s² + 2.32561305242455s + 1.532776121137
s + 1.21497965956963
8
(Q = 1.22567) s² + 1.28299239215439s + 2.47283345436118
(Q = 0.71085) s² + 1.9741153642581s + 1.96926212166436
(Q = 0.55961) s² + 2.35216938769735s + 1.73263396575613
(Q = 0.50599) s² + 2.52527503176501s + 1.6326875194579
9
(Q = 1.32191) s² + 1.25882651612532s + 2.76908688019576
(Q = 0.76061) s² + 1.95987915089682s + 2.22220333341006
(Q = 0.58941) s² + 2.36803531877968s + 1.94807468608236
(Q = 0.51971) s² + 2.58984069125509s + 1.81161516486553
s + 1.33033917731169
10
(Q = 1.41531) s² + 1.2383906778965s + 3.07197590340822
(Q = 0.80977) s² + 1.9463531040995s + 2.48421464566909
(Q = 0.62047) s² + 2.37707641403698s + 2.17534467756742
(Q = 0.53755) s² + 2.63510305440823s + 2.00648730986839
(Q = 0.50391) s² + 2.75729393738485s + 1.9305310305774
Yes, -3dB tables 🙂I suspect that the Bessel tables to which you refer generate Bessel filters that are -3 dB at your specified cutoff frequency, not -6 dB. Correct? I am so accustomed to using -6 dB Bessel filter equations that I forget I had to generate them myself.
- Home
- Loudspeakers
- Multi-Way
- Why not IIR filters + a global phase linearization by FIR