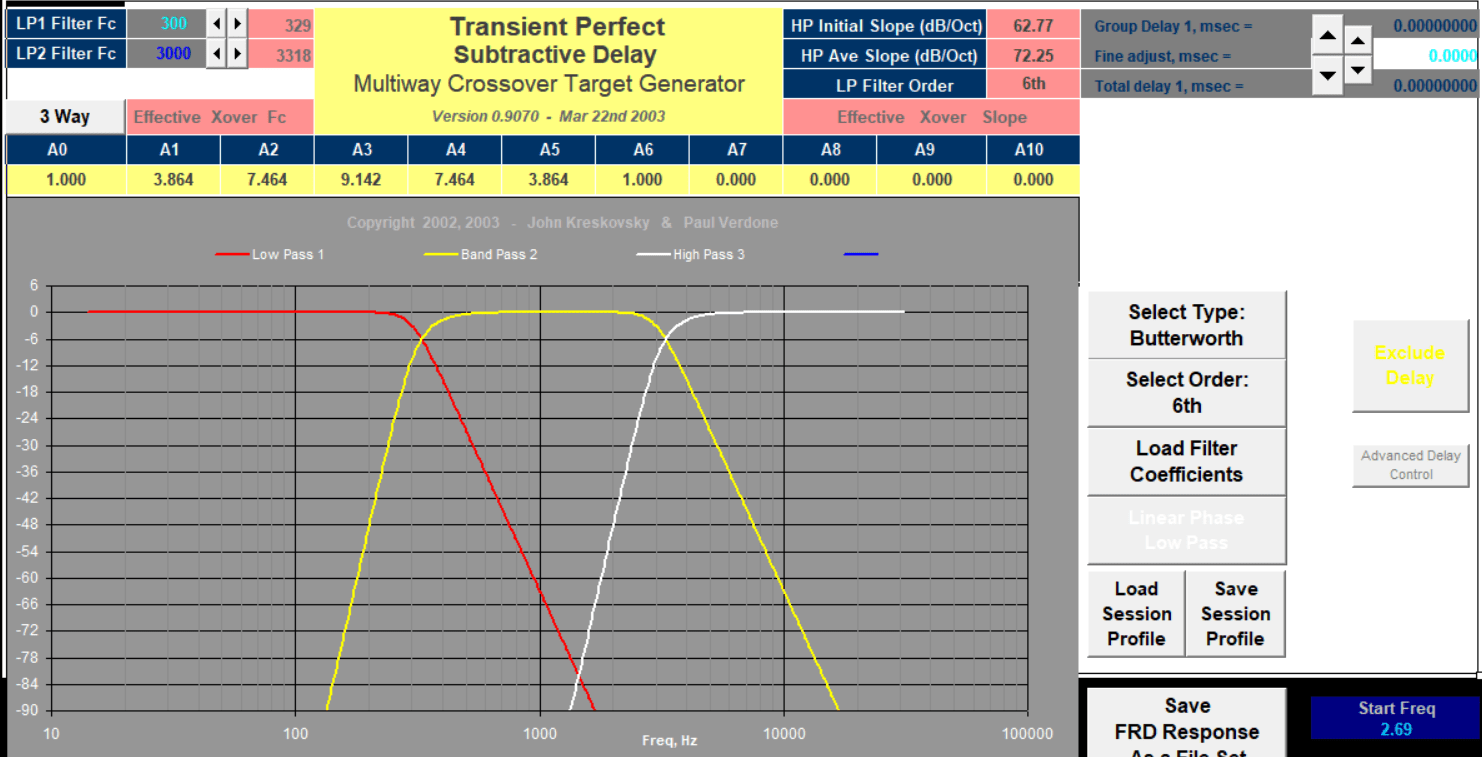
Years ago I had developed a spread sheet for 2-way subtractive delay crossover. It allowed yuo to choose the crossover point, low pass filter type and order, and whether the LP filter was linear or minimum phase. Later, Paul V of the old FRC took it s a step further and made it more general, allowing up to a 4-way crossover. It seems to have some glitches in it but is still functional. It includes Butter worth filters and show what I found that when using a linear phase, Butterworth LP section the subtractive HP section roll off at a slope twice that of the LP section. Here is a screen shot of the crossover section for a 3-wy using 6th order Butterworth amplitude LP sections with linear phase. Attached is the spread sheet. Don't know how well it will work with newer Excel, but fun to play with if it works.
Trying to catch-up with all of the requests. The forum limits the number of replies per hour, so I'll have to wait a bit to get to the remainder. If you requested a copy of the paper but haven't received it by tomorrow, write to me again and I'll give it another try.
- Greg
- Greg
True, but it's still a pain to use -- like learning another language. I use LaTeX, pronounced "lay-TEK". Only I call it "cave-tech".
Same here, but I use this thing called LyX that looks like MS Word but generates LaTeX output once you press a button. There are also many built-in templates available within LyX for letters, papers, presentations (beamer) e.g. IEEE transactions. One just needs to install LyX and specify the path of the MikTeX package that's it, freeware no money.
https://www.lyx.org/
Almost all of those old FRC Excel based programs work fine with newer versions of Excel, but only if you install the 32 bit version of Office instead of the 64 bit version. On my Win 11 machine I have both Excel 2010 (32 bit) and Excel 2021 (64 bit) although MS doesn't support multiple Office versions. A perhaps cleaner and safer way (which I used in the past) is to create a virtual machine (I used good old Windows 7) to run the 32 bit version of Office. What ever works for you.
I did find a slightly newer version of the app on the old FRC website via the way back machine (LINK). The TPSD (Transient Perfect Subtractive Delay) file, tpsd1.10.exe, is a self-extracting executable that contains TPSDMulti-.9071.xls, a user manual and fftdll.dll. The DLL speeds up the FFT process, but probably isn't needed on today's machines.
I'm on Office Enterprise 2007, got the following upon opening the spreadsheet, dismissed it (End). But most buttons worked and I was able to see some graphs as expected. Thanks.
To everybody who received a copy of my Matched Delay Crossover Tutorial, and anybody who still wants to:
It's been a few days since I received any new feedback (thank you!), so I'm declaring the document to be finished. The final version is 20231026. If you have a version earlier than that, and want a copy of the final version, please PM me.
All of the changes are what I would call "cosmetic" -- typographical errors, language clarification, tidying-up some graphics, etc., so if you have an earlier version you still have all of the correct technical information.
It's been a few days since I received any new feedback (thank you!), so I'm declaring the document to be finished. The final version is 20231026. If you have a version earlier than that, and want a copy of the final version, please PM me.
All of the changes are what I would call "cosmetic" -- typographical errors, language clarification, tidying-up some graphics, etc., so if you have an earlier version you still have all of the correct technical information.
Hi Greg, I've enjoyed your paper. It has a nicely laid out logical progression, that i found easy to understand.
Other than when I needed my long forgotten math (lol/sigh).
Oh, what's the practical meaning of RMS periods? ...I couldn't grasp that either...
The "G8x2" does look like a nice substitute for a Gaussian low pass. I could see that being used anywhere a second order high pass works.
I like your idea of trying to minimize impulse response width per bandwidth. I've never really thought of that.
I see my FIR generating software will produce the subtractive complement for linear phase bessels, BW's, and a host of other non-complementary types. ( and from either side)
I may play with lin phase Bessel's despite their relatively low orders vs the high orders i typically swear by......
i figure we never know, proof is in the listening...gotta keep trying stuff.
Must admit though, I have a hard time imagining that reduced impulse widths will overpower the benefits of reduced lobing frequency ranges.
Maybe like all things in audio, there's a happy compromise.....🙂
Anyway, thx again !
Other than when I needed my long forgotten math (lol/sigh).
Oh, what's the practical meaning of RMS periods? ...I couldn't grasp that either...
The "G8x2" does look like a nice substitute for a Gaussian low pass. I could see that being used anywhere a second order high pass works.
I like your idea of trying to minimize impulse response width per bandwidth. I've never really thought of that.
I see my FIR generating software will produce the subtractive complement for linear phase bessels, BW's, and a host of other non-complementary types. ( and from either side)
I may play with lin phase Bessel's despite their relatively low orders vs the high orders i typically swear by......
i figure we never know, proof is in the listening...gotta keep trying stuff.
Must admit though, I have a hard time imagining that reduced impulse widths will overpower the benefits of reduced lobing frequency ranges.
Maybe like all things in audio, there's a happy compromise.....🙂
Anyway, thx again !
Just as we quantify the "center" and "width" of a distribution of things with mean and standard deviation, we quantify the "center" and "length" of a signal with "central time" and "RMS duration". We can't use standard deviation directly with signals, because standard deviation requires that the values being included in the computation can never be negative. Of course, AC signals like audio have both positive and negative values, so we must square the signal to ensure that the values being included in the computation are never negative. Otherwise, the principle is the same -- large standard deviation means that the distribution is "spread out"; large RMS duration means that the signal lasts a long time.
I’ve been interested how subtractive delay filters would use the meager ADAU1701 DSP resources and how they would perform in an inexpensive 1701 DSP board. So, I designed two, single-channel, three-way subtractive crossovers: Gregory Berchin’s simplified 8th order Bessel and John Kreskovsky’s 6th order Butterworth. Each of the three crossover outputs were measured and then added together to check for their summed frequency and phase responses.
Both crossovers have nearly identical crossover frequencies of ~250 and ~2100 Hz. The first two attachments are the SigmaStudio crossover schematics with the compiler resource usage statistics added as comments. The third attachment shows the individual measured outputs of both filters. The filters’ responses track quite well up to ~50 dB below the fundamental, but below that level the high pass filters’ responses begin to lose track. The fourth and fifth attachments show the filters’ frequency and phase responses when the individual outputs are summed together. Linear phase!
Overall, I’m quite impressed with the performance of both filters. They offer a way to achieve linear phase filters for users of the ubiquitous 1701 DSP. Special thanks to Gregory and John for their work on these filters. It’s been 20+ years since their initial development, but better late than never!
Details, details……
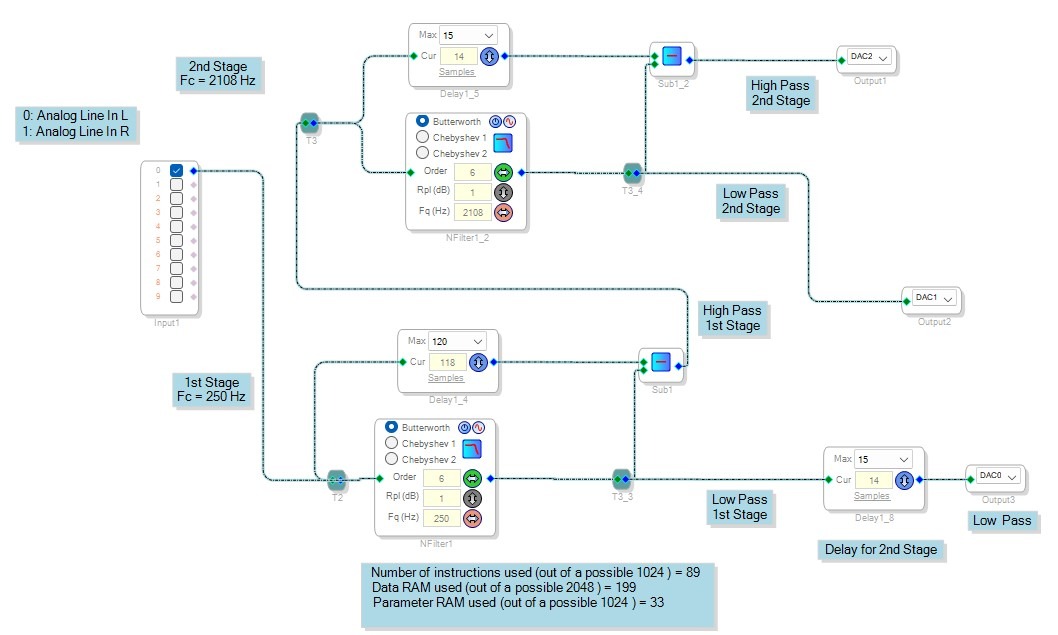
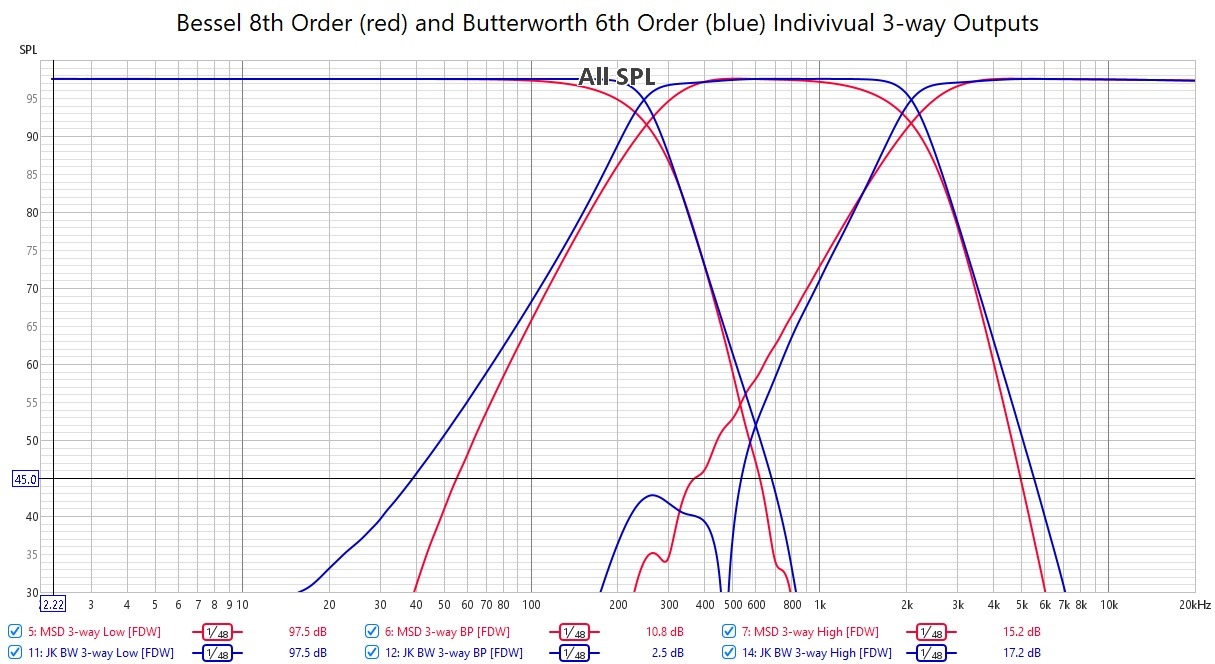
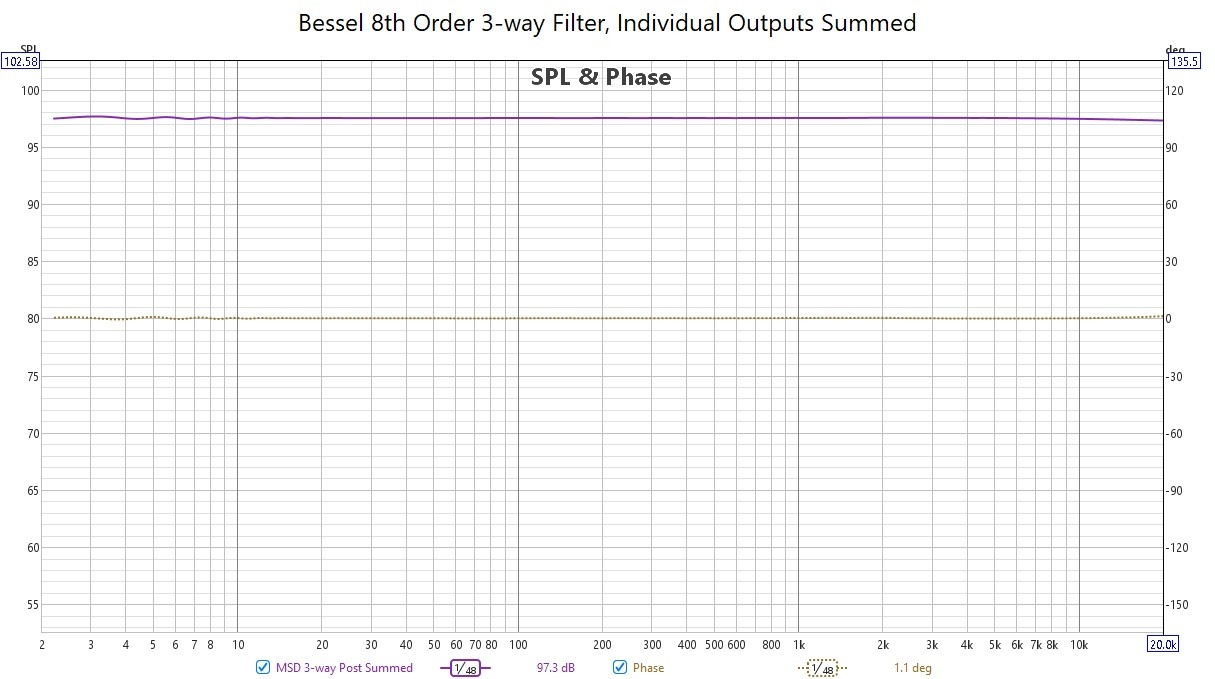
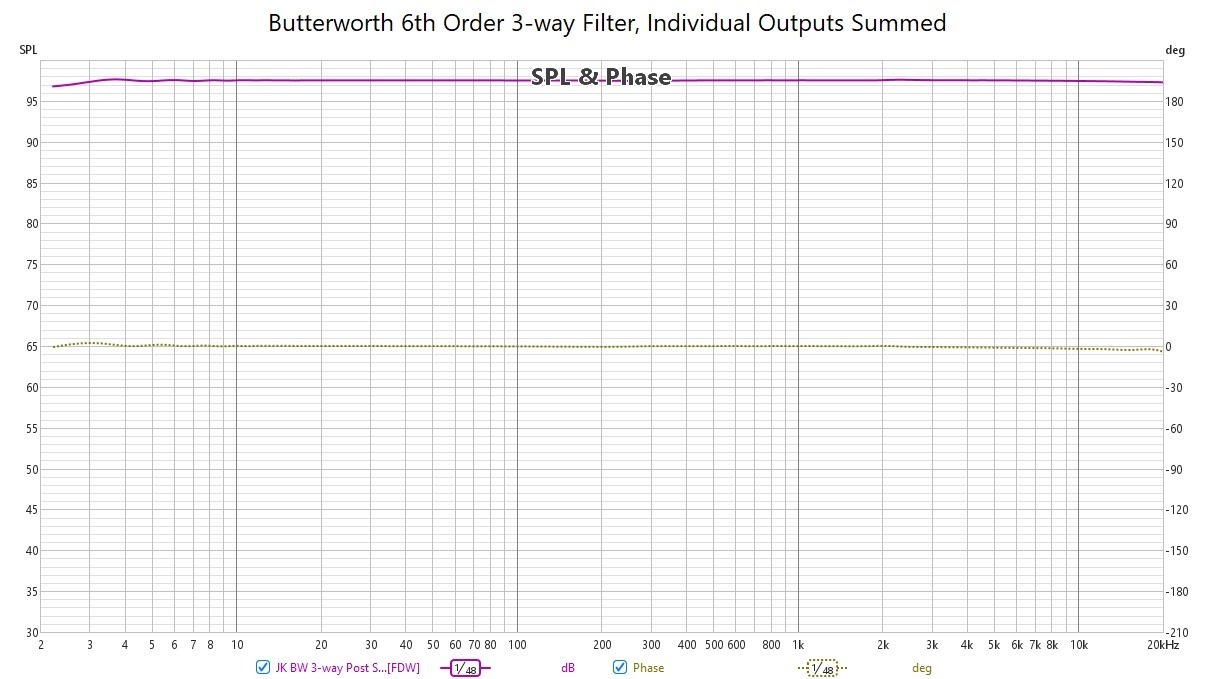
Both crossovers have nearly identical crossover frequencies of ~250 and ~2100 Hz. The first two attachments are the SigmaStudio crossover schematics with the compiler resource usage statistics added as comments. The third attachment shows the individual measured outputs of both filters. The filters’ responses track quite well up to ~50 dB below the fundamental, but below that level the high pass filters’ responses begin to lose track. The fourth and fifth attachments show the filters’ frequency and phase responses when the individual outputs are summed together. Linear phase!
Overall, I’m quite impressed with the performance of both filters. They offer a way to achieve linear phase filters for users of the ubiquitous 1701 DSP. Special thanks to Gregory and John for their work on these filters. It’s been 20+ years since their initial development, but better late than never!
Details, details……
- I created a zip file containing both SigmaStudio projects which can be downloaded HERE.
- I used THIS TinySine DSP board with Fs set to 48 KHz. I used REW for measuring, also at 48 KHz. The DSP board’s native frequency response rolled off at the upper and lower ranges which affected the phase. I converted the native response into a “microphone” calibration formatted file which resulted in a totally flat frequency and phase response using a “straight through” (input directly to DAC) project.
- Don’t use the SigmaStudio “Fractional Delay” as it causes phase shift in the higher frequencies. See these links for details (LINK1, LINK2). Use the standard delay which delays integer multiples of 1/Fs.
- The SigmaStudio “Simulation Probe” doesn’t correctly display the filter’s phase. The magnitude is displayed correctly though.
- The 1701 DACs output in negative polarity. See the 1701 datasheet for details.
- I used SigmaStudio’s “Nth Order” filter for the Butterworth filter and John’s Excel worksheet for the Butterworth delay times. I used SigmaStudio’s “Parametric EQ” and selected four “General Low Pass” filters for the 8th order Bessel filter. Their Q values and frequencies along with their delay values were calculated from posts in this thread.
If a copy is still available I would appreciate it, thank you for the many educational posts, and I have one question.
I'd like to discuss in terms of continuous time initially, so minimum phase by default and more or less like IIR, add the additional complexity of sampled systems once I understand more clearly.
The simple (no time delay) subtractive crossover is usually exemplified with the output of a low pass filter (LPF) subtracted from full bandwidth channel to create the HP.
It is possible to do the reverse, subtract HPF output to create the LP.
This turns out to have benefits.
The HPF can be sharper to better protect the tweeter, while the derived, slower cut-off output is then the LPF and the woofer can handle a 6 db/octave slope better.
(A 6dB/octave HPF slope doesn't even seem physically possible to maintain, SPL is proportional to cone/dome acceleration,and if that falls by 6 dB/octave as frequency drops then the velocity will be flat, and the displacement increases as the frequency falls, surely).
Similarly, the classic Lipshitz & Vanderkooy paper describes the time delay subtractive crossover also with an LPF and subtraction.
Can an equivalent HDF subtraction version be created?
There would seem to be benefits, not as dramatic because the derived (HPF) is sharper in the time delayed version, but still useful.
Also, inaccuracies in the system parameters, say from component errors or imperfections in the subtractor, cause the derived filter slope to plateau, so it would be desirable this be in the filter to the more robust speaker, the woofer.
Your 'improved' method does create a LP from a HP, that was in turn created from a LP, and this implies this can be done in the continuous time case, but I haven't seen anyone do it, or an analysis.
To do it in one step may not be ideal, specifically if one wants to use a Bessel filter, because I suspect there is some LPF/HPF asymmetry.
(Because filters themselves are usually specified from a LP prototype and the HP derived mathematically from it, and the Bessel is a bit atypical)
Perhaps it will be clearer to me if can I read your tutorial, otherwise it's back to the library to reread Lipshitz and Vanderkooy tomorrow.
Best wishes
David
Last edited:
The classic subtractive crossover (also called constant voltage crossover) can also be done by subtracting the highpass output from the input. You can also subtract the sum of a highpass and a lowpass form the input signal in order to get a three-way crossover where the midrange is the derived path. Furthermore it is possible to build these crossovers with any order you like. But this all has a downside: There are humps in the transfer functions of the outputs. And there is overlap in the crossover region. The higher the filter order the more extreme does it get. And we haven't yet started about taking the driver transfer functions into consideration.
In principle these crossover can be used in some cases but getting there is not that easy. I once used something like that with a FAST topology. But in order to thake the driver transfer functions into consideration I didn't use subtraction but achieved the transfer functions of such a crosover in a more direct fashion.
The reason why the subtractive delay crossover is subtracting the lowpass from the highpass is the group delay properties of the filters involved. An analog or IIR lowpass has a more or less constant group-delay within its pas pand while the "constant" group-delay region of a higpass lies below its passband. It would certainly be nice if it was different. But sometimes the laws of physics don't like us .... The downside of the classic subtractive delay crossover is the fact that one can use very steep lowpass filters but the drived highpass filters don't get steeper than thirt order.
That's where gberchin's trick comes into play. He uses two (one could even use more) subtractive-delay generated higpass filters with constant grop-delay to derive the final lowpass filter. I will definitely try this one day as well.
To your last question: Yes there were attempts to build subtractive delay crossovers with analog circuitry. One example is an old studio monitor by Studer professional. It was an "allpass massgrave" with tons of NE5532 op-amps.
Regards
Charles
In principle these crossover can be used in some cases but getting there is not that easy. I once used something like that with a FAST topology. But in order to thake the driver transfer functions into consideration I didn't use subtraction but achieved the transfer functions of such a crosover in a more direct fashion.
The reason why the subtractive delay crossover is subtracting the lowpass from the highpass is the group delay properties of the filters involved. An analog or IIR lowpass has a more or less constant group-delay within its pas pand while the "constant" group-delay region of a higpass lies below its passband. It would certainly be nice if it was different. But sometimes the laws of physics don't like us .... The downside of the classic subtractive delay crossover is the fact that one can use very steep lowpass filters but the drived highpass filters don't get steeper than thirt order.
That's where gberchin's trick comes into play. He uses two (one could even use more) subtractive-delay generated higpass filters with constant grop-delay to derive the final lowpass filter. I will definitely try this one day as well.
To your last question: Yes there were attempts to build subtractive delay crossovers with analog circuitry. One example is an old studio monitor by Studer professional. It was an "allpass massgrave" with tons of NE5532 op-amps.
Regards
Charles
The short answer is "yes", and section 3 of the paper shows a way to do it. But it's not an intuitive configuration.
I'll try to describe the problems with deriving the LPF from the HPF with some general examples:
Consider a Gaussian filter prototype, and a discrete-time (digital) implementation. If using a 1 kHz Gaussian LPF as the basis for an MDS crossover, then the response is 1.0 at DC, 0.5 at 1 kHz, and the Gaussian "tail" has the entire span between 1 kHz and half the sampling frequency to work its way toward zero, e.g., 21050 Hz in a 44100 Hz sampling context. However, if using a 1 kHz Gaussian HPF as the basis for an MDS crossover, then the response is 1.0 at half the sampling frequency, 0.5 at 1 kHz, and not much less than 0.5 at DC -- not a very effective HPF.
Now consider using a more traditional HPF for the prototype, perhaps an IIR Bessel HPF with response approximately 1.0 at half the sampling frequency, 0.5 at 1 kHz, and zero at DC. That will work, but the impulse response of that Bessel HPF oscillates quite a lot. Thus the derived LPF will also exhibit exactly the same impulse response oscillations, out-of-phase with those of the HPF. So while mathematically possible, the resulting crossover will not be very practical.
Thank you, @phase_accurate , this is a point that needs to be made more often. It is the reason that, for example, a Bessel LPF has such a nice impulse response, while a Bessel HPF oscillates like crazy.
You are welcome.
While re-reading my post I've just seen that I made an awful lot of typos. 😳
Regards
Charles
While re-reading my post I've just seen that I made an awful lot of typos. 😳
Regards
Charles
Yes, I mentioned this in my post, that is more or less the point.
There is a hump in the derived output, that's why it should be better to define the HPF and derive the LP because the woofer should handle the peak more comfortably.
If you do that then the crossover looks borderline acceptable, certainly better than the traditional "subtract the LPF".
Yes, I understand that, but it's not clear to me yet whether we can do the same trick as for the simple subtractive crossover, and improve it if we define the HPF and derive the LP.
In filters there is usually a duality possible, replace 's' with '1/s' in the Laplace equations etc.
So my first idea was to define the HPF, add a time adjustment to the input and subtract to produce the LP, just the dual of the standard version.
The time adjustment would be the group delay of the HPF, just as in the the canonical version it's the delay of the LPF.
But the group delay of the HPF is not a "delay", and decreases towards zero, so I'm not sure it's realizable.
As far as I can see he adjusts only for the explicitly included delay blocks.
I don't understand how this would work in a simpler case, with an explicitly specified HPF.
I think it would need a filter defined to keep the group delay close to zero as far down as frequency decreases, presumably below the crossover point, like the inverse of an LP Bessel that tries to keep the group delay constant as far as possible as frequency increases.
Does that make sense and does such a filter exist or have a name?
My question was whether anyone had done a subtractive delay crossover with a defined HPF and the LP derived from that, as described above. The dual of Lipshitz & Vanderkooy, similar to Berchin's but continuous time.
Best wishes
David
Last edited:
You could get rid of the hump quite easily, keep reading.
It is easily realisable, just replace the "delay" with an all-pass filter of the same phase as the highpass filter.
Yes, please see below ... It's LR4 not Bessel, but Bessel must be similar, except for that the symmetry won't be there.
If you follow MATLAB or Octave, here is the code. Hope that helps.
Code:
% LOWPASS
freq = 100;
Q = 0.7071;
wc = 2*pi*freq; % Cutoff frequency
but_sys = tf([wc*wc],[1, wc/Q, wc*wc]); % analogue lowpass transfer function
lp_sys = but_sys*but_sys; % BUT2 to LR4
%HIGHPASS
freq = 100;
Q = 0.7071;
wc = 2*pi*freq; % Cutoff frequency
but_sys = tf([1,0,0],[1, wc/Q, wc*wc]); % analogue lowpass transfer function
hp_sys = but_sys*but_sys; % BUT2 to LR4
%ALLPASS (half-order, same Q)
freq = 100;
Q = 0.7071;
wc = 2*pi*freq; % Cutoff frequency
ap_sys = tf([1, -wc/Q, wc*wc],[1, wc/Q, wc*wc]); % analogue allpass transfer function
% BODE PLOT DISPLAY
options = bodeoptions;
options.FreqUnits = 'Hz';
options.XLim = [1,20000];
options.YLim = [-360, 0];
options.grid = 'On';
options.Freqscale ='Log';
%options.MagVisible = 'Off';
options.PhaseWrapping = 'Off';
options.PhaseMatching = 'On';
figure(1)
bode(hp_sys,ap_sys-hp_sys,options);
Last edited:
I guess with FIR based crossovers this has been done already because you can easily design those for constant group-delay. But I don't know any case where this has been done with IIR or analog highpass filters. There is quite some effort needed to EQ those to flat group-delay so it isn't impossible but it does most probably not pay off.
That is certainly true for the standard asymmetric case where the derived path is only first order, If you use topologies where both crossover branches are of higher order than first order than you would have humps in both branches.
Agreed ! See the thread that I have linked to. You would need a sturdy "tweeter" (in my case it was a wideband driver) and a woofer that is reasonably behaved on top.
I wanted to design an example with nicely priced and easily obtainable drivers for a long time already but did not find the time so far.
Regards
Charles
This is Bessel, see code for details..
Code:
%LOWPASS
freq1 = 141.92;
Q1 = 0.5219;
wc = 2*pi*freq1;
bq1 = tf([wc*wc],[1, wc/Q1, wc*wc]); % analogue lowpass transfer function
freq2 = 159.12;
Q2 = 0.8055;
wc = 2*pi*freq2;
bq2 = tf([wc*wc],[1, wc/Q2, wc*wc]); % analogue lowpass transfer function
lpf = bq1*bq2; % Bessel LPF
%HIGHPASS
freq1 = 141.92;
Q1 = 0.5219;
wc = 2*pi*freq1;
bq1 = tf([1,0,0],[1, wc/Q1, wc*wc]); % analogue lowpass transfer function
freq2 = 159.12;
Q2 = 0.8055;
wc = 2*pi*freq2;
bq2 = tf([1,0,0],[1, wc/Q2, wc*wc]); % analogue lowpass transfer function
hpf = bq1*bq2; % Bessel HPF
%ALLPASS
freq = sqrt(freq1*freq2);
Q = sqrt(Q1*Q2);
wc = 2*pi*freq;
apf = tf([1, -wc/Q, wc*wc],[1, wc/Q, wc*wc]); % analogue allpass transfer function
% DISPLAY
options = bodeoptions; % bode plot
options.FreqUnits = 'Hz';
options.XLim = [1,20000];
options.YLim = [-450,20];
options.grid = 'On';
options.Freqscale ='Log';
%options.MagVisible = 'Off';
options.PhaseWrapping = 'Off';
options.PhaseMatching = 'On';
figure(1)
bode(hpf,apf-hpf,options); % LPF obtained by subtraction