What is the steepest realistic audio transient in terms of V/us?

[benb]

Can you *please* stop calling "RMS" the Volts we are talking about?

And furthermore:

We say the same.

100 Wrms at 8 Ohms => 28,28 Vrms x1,41 = 39.9 V (or Vp).

Volts RMS into a resistor does NOT result in Watts RMS, regardless of what the FTC said in 1974.

Well if you limit your audio bandwidth to 20kHz nothing in that band can be faster than a 20kHz sine wave full level.

This is hardly pertinent to this thread, but there's a difference here - "intentional" bandwidth limiting is (usually) done with a low pass filter which only affects frequency balance, but slew rate limiting is a nonlinear process, and (additionally) causes harmonic distortion. I recall seeing a triangle wave on a scope from a 741 opamp output with a sine wave input in a college EE lab circa 1978.

Mind. Blown. Six pages of posts following a question that was answered in Post #2. 🙂

Set your settings (I forget exactly where it is) to 50 posts per page, and you'll find we're only on page two of this nonsense. 🙂

 

[cbdb]

Slew rate is the speed an amp comes out of overdrive into linear region. And has very little to do with the linear region once it's there. A square wave is faster than the feedback so the input gets overloaded.

 

[AndrewT]

Slew rate is the speed an amp comes out of overdrive into linear region. And has very little to do with the linear region once it's there. A square wave is faster than the feedback so the input gets overloaded.

Leach talks about this in his Lo Tim papers.

 

[maty tinman]

sound better with 80 V/uS than 8 V/uS?

The question is if the same 100W amplifier with 8, 16, 20, 40... V/uS has the same sound in a good system (with RFI/EMI and DC cleanned) when plays orchestral music.

Is the sound better with 80 V/uS than 8 V/uS?

By the way, why the bandwith limiter is not always about 20Khz?

 

[AndrewT]

kHz not Khz
k= kilo
K = Kelvin
Hz= Hertz
h = hecto
z = ?

Khz is nonsense. Just like your other misused units.

 

[maty tinman]

You are right. And a grandmother is not a bike too, but...

Again, is the sound better with 80 V/uS than 8 V/uS?

Why the bandwith limiter is not always about 20 kHz?

 

[bimo]

This is hardly pertinent to this thread, but there's a difference here - "intentional" bandwidth limiting is (usually) done with a low pass filter which only affects frequency balance, but slew rate limiting is a nonlinear process, and (additionally) causes harmonic distortion. I recall seeing a triangle wave on a scope from a 741 opamp output with a sine wave input in a college EE lab circa 1978.

I tried an amplifier with different slew rate (I change the compensation), to find slew rate effect at listening test.
I believed that the required slew rate is aprox. 1Vp/V/uS. But now, it change after I done my experiment.

You should try it your self. It is difficult to change slew rate without change the other parameter. But I did my best...

Bandwidth limiting (using filter) is different than slew rate limiting.

 

[jan.didden]

Hi Guys

The concept of superposition of sine waves is pretty old and most people see it in high school math, so why is it so "alien" here?

A prime example is a square wave. A square wave is a specific series of sine waves with specific amplitudes. The fundamental is just the same frequncy as the final square wave. The harmonics of this frequency are all odd-order and have an amplitude that is the reciprocal of their order. For example, the third harmonic is at one-third the amplitude of the fundamental; the fifth harmonic is one-fifth the amplitude,and so on.

As you superimpose each harmonic over the fundamental, the slope of the leading edge of the composite wave becomes steeper. In a properly scaled drawing of a sine wave the zero-cross slope is actually 45-degrees, but as you superimpose further frequencies the slope approaches 90-degrees. This is just high-school math, as I said. Not complicated enough for some around here, I guess.

Music superimposes many frequencies at a time. If it did not, the envelope of the sound would not be as it is - uncompressed sounds have transient attack that is up to four times the amplitude of the sustain part of the envelope, but more typically just twice as high. Because the superposition dramatically steepens the slope of the leading edge, it is pretty much a necessity that an audio circuit have fast response and that this response be much faster than simply passing the highest sine frequency demands.

Have fun

Sigh. This is not true is the system is bandwidth limited like audio. In that band, the higher harmonics that contribute to the ever increasing steepness, are simply not there. So the steepness is ultimately limited by the bandwidth, as explained here over and over again.

High school math is good - thinking is better 😉

Jan

 

[SY]

Sigh. This is not true is the system is bandwidth limited like audio.

All source material is bandwidth limited. Digital for 99% of the world because of anti-aliasing and reconstruction, analog because of tape recorders and microphones.

Fourier denial is a weird thing.

 

[hypertiger]

Hi Guys

The concept of superposition of sine waves is pretty old and most people see it in high school math, so why is it so "alien" here?

A prime example is a square wave. A square wave is a specific series of sine waves with specific amplitudes. The fundamental is just the same frequncy as the final square wave. The harmonics of this frequency are all odd-order and have an amplitude that is the reciprocal of their order. For example, the third harmonic is at one-third the amplitude of the fundamental; the fifth harmonic is one-fifth the amplitude,and so on.

As you superimpose each harmonic over the fundamental, the slope of the leading edge of the composite wave becomes steeper. In a properly scaled drawing of a sine wave the zero-cross slope is actually 45-degrees, but as you superimpose further frequencies the slope approaches 90-degrees. This is just high-school math, as I said. Not complicated enough for some around here, I guess.

Music superimposes many frequencies at a time. If it did not, the envelope of the sound would not be as it is - uncompressed sounds have transient attack that is up to four times the amplitude of the sustain part of the envelope, but more typically just twice as high. Because the superposition dramatically steepens the slope of the leading edge, it is pretty much a necessity that an audio circuit have fast response and that this response be much faster than simply passing the highest sine frequency demands.

Have fun

😱

How about NO?!

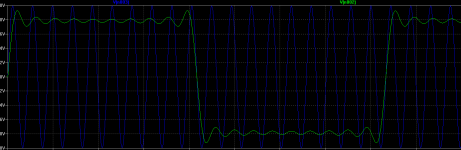
I'm attaching a picture, there is a 20 Hz square wave up to its 19-th harmonic and a 19*20 Hz sine wave at full amplitude.

Please compare slew rates, it's not that hard.

Have fun

 

[DF96]

A prime example is a square wave. A square wave is a specific series of sine waves with specific amplitudes. The fundamental is just the same frequncy as the final square wave. The harmonics of this frequency are all odd-order and have an amplitude that is the reciprocal of their order. For example, the third harmonic is at one-third the amplitude of the fundamental; the fifth harmonic is one-fifth the amplitude,and so on.

As you superimpose each harmonic over the fundamental, the slope of the leading edge of the composite wave becomes steeper. In a properly scaled drawing of a sine wave the zero-cross slope is actually 45-degrees, but as you superimpose further frequencies the slope approaches 90-degrees. This is just high-school math, as I said. Not complicated enough for some around here, I guess.

Music superimposes many frequencies at a time. If it did not, the envelope of the sound would not be as it is - uncompressed sounds have transient attack that is up to four times the amplitude of the sustain part of the envelope, but more typically just twice as high. Because the superposition dramatically steepens the slope of the leading edge, it is pretty much a necessity that an audio circuit have fast response and that this response be much faster than simply passing the highest sine frequency demands.

You started so well, with undeniable facts. Sadly you gradually moved from facts into myths.

Having for a brief while believed (on the basis of a flawed mathematical analysis) that a band-limited low frequency square wave needs more slew rate than a maximum frequency sine wave, I now believe (on the basis of a correct mathematical analysis) that the maximum slew rate is the sine wave. I say this because I can't conceive of a faster slew rate (before bandlimiting) than a square wave - music waveforms don't even come close.

People need to stop hand-waving; only physicists are licensed to do that and they know about mathematics and orders-of-magnitude. If someone believes that they can invent a bandlimited signal with faster slew rate than a max freq sine wave then let them offer proof by construction. If they are right then I will believe them.

 

[DF96]

Slew rate is the speed an amp comes out of overdrive into linear region. And has very little to do with the linear region once it's there. A square wave is faster than the feedback so the input gets overloaded.

That is better known as 'slew rate limit'. Slew rate is the maximum rate of change of a signal.

 

[jan.didden]

I'm attaching a picture, there is a 20 Hz square wave up to its 19-th harmonic and a 19*20 Hz sine wave at full amplitude.

Please compare slew rates, it's not that hard.

Have fun

Nice!

Jan

 

[forr]

The concept of superposition of sine waves is pretty old and most people see it in high school math, so why is it so "alien" here?

A prime example is a square wave. A square wave is a specific series of sine waves with specific amplitudes. The fundamental is just the same frequncy as the final square wave. The harmonics of this frequency are all odd-order and have an amplitude that is the reciprocal of their order. For example, the third harmonic is at one-third the amplitude of the fundamental; the fifth harmonic is one-fifth the amplitude,and so on.

As you superimpose each harmonic over the fundamental, the slope of the leading edge of the composite wave becomes steeper. In a properly scaled drawing of a sine wave the zero-cross slope is actually 45-degrees, but as you superimpose further frequencies the slope approaches 90-degrees. This is just high-school math, as I said. Not complicated enough for some around here, I guess.

Music superimposes many frequencies at a time. If it did not, the envelope of the sound would not be as it is - uncompressed sounds have transient attack that is up to four times the amplitude of the sustain part of the envelope, but more typically just twice as high. Because the superposition dramatically steepens the slope of the leading edge, it is pretty much a necessity that an audio circuit have fast response and that this response be much faster than simply passing the highest sine frequency demands.

A square signal can seen as a series of odd harmonics in synchronism.

Non-electronic instruments deliver even and odd harmonics, the synchronism of which is certainly not rock-steady.

 

[jan.didden]

Originally Posted by cbdb
A square wave is faster than the feedback so the input gets overloaded.

Only in a badly designed amp; it's a non-issue in a competent design.

jan

 

[Struth]

Hi Guys

Who said it has to be a 20kHz squarewave? How about 1kHz? or 100Hz? Look at the real world tests made on amplifiers and you see amps with good square wave response and thus good rise times despite bandwidth limiting to be free of RF and other extraneous noise. Some here are intent on arguing for the sake of it, or making things more complex than reality.

Have fun

 

[SY]

Who said it has to be a 20kHz squarewave?

No-one did. No program material contains it, no mike used in music recording can pick that up, and no commercial loudspeaker can reproduce it. If you have a bandwidth limit- and you do in audio- it's a complete irrelevancy. So the statement "it is pretty much a necessity that an audio circuit have fast response and that this response be much faster than simply passing the highest sine frequency demands" is just not correct.

 

[hypertiger]

Hi Guys

Who said it has to be a 20kHz squarewave? How about 1kHz? or 100Hz?

What about 1 kHz or 100 Hz? Do you want me to provide an example of 100 Hz / 1 kHz square wave approximation? Do you think changing fundamental frequency of sq. wave affects FT?

Look at the real world tests made on amplifiers and you see amps with good square wave response and thus good rise times despite bandwidth limiting to be free of RF and other extraneous noise.

Using a square wave test signal has nothing to do with the topic being discussed. It's merely a very convenient way to test an amp.

Some here are intent on arguing for the sake of it, or making things more complex than reality.

Have fun

Indeed, someone here makes false claims and ignores real life examples 😉

 

[DF96]

Who said it has to be a 20kHz squarewave?

Not me. I don't recall anyone saying that.

 

[Struth]

Hi Guys

Post-58 referred to a 20kHz squarewave. I never did.

Others have referred to transients without being flamed - is it because one of them is a mod?

Band limiting at 20kHz means response is only flat to 2kHz - not much of a hifi. Look at the wave forms in APAD6.

Debate amongst yourselves.

Have fun