I used to fly bass horns as much as 50 foot high, the chain motors had 60 foot lift.
Lots of touring systems are flying subs even higher now, seems arenas are being built taller.
So, the inverse square loss starts just outside the box where the horn's terminus occurs, for 2 Pi space: 1/2 diagonal X 1.33.
Sounds correct to me, where is the information you quote from ?
Art Welter
Last edited:
So my understanding is you believe the position where sound begins to falloff inversely to the distance is just outside the mouth?
That's your answer? That's what you're saying?
No matter what the flare rate, mouth size or internal path length, no matter what the frequency, you believe the place where inverse pressure attenuation begins is at the mouth.
That's what you're saying?
That's your answer? That's what you're saying?
No matter what the flare rate, mouth size or internal path length, no matter what the frequency, you believe the place where inverse pressure attenuation begins is at the mouth.
That's what you're saying?
Now i see, You're confusing Inverse square law with Inverse distance law.
The reflective inner surface of the horn keeps the inverse distance law from applying until the wave energy is free from reflections. i.e. outside the effective length of the horn.
from: The inverse distance law 1/r for the sound pressure - no square - acoustic audio sound reduction free field particle amplitude volume loudness level distance laws dB decibel calculator distance dropratio- sengpielaudio Sengpiel Berlin
"In the real world, the inverse distance law p ~ 1/r is always an idealization because it assumes exactly equal sound pressure p as sound field propagation in all directions. If there are reflective surfaces in the sound field, then reflected sounds will add to the directed sound and you will get more sound at a field location than the inverse distance law predicts. If there
are barriers between the source and the point of measurement, you may get less than the distance law predicts. Nevertheless, the inverse distance law is the logical first estimate of the sound pressure you would get at a distant point in a reasonably open area. The reference sound pressure level SPL = 0 dB is the sound pressure of p0 = 20 µPa = 20 × 10-6 Pa = 2 × 10-5 Pa or 2 × 10-5 N/m2."
ref: Multimedia Audio Course - Decibels - Inverse distance law - Sound engineering - Audiosonica
from wiki: Acoustics
In acoustics one usually measures the sound pressure at a given distance r from the source using the 1/r law.[6] Since intensity is proportional to the square of pressure amplitude, this is just a variation on the inverse-square law.
Example
In acoustics, the sound pressure of a spherical wavefront radiating from a point source decreases by 50% as the distance r is doubled; measured in dB, the decreases is still 6.02 dB, since dB represents an intensity ratio. The behaviour is not inverse-square, but is inverse-proportional (inverse distance law):
The same is true for the component of particle velocity that is in phase to the instantaneous sound pressure :
Only in the near field is there a quadrature component of the particle velocity 90° out of phase with the sound pressure, which thus does not contribute to the time-averaged energy or the intensity of the sound. The sound intensity is the product of the RMS sound pressure and the RMS particle velocity (the in-phase component), both of which are inverse-proportional. Accordingly, the intensity follows an inverse-square behaviour:
Wayne,
With no quotes I'm not sure who you are responding to, but I agree with what revboden wrote:
“The inverse square loss starts just outside the box where the horn's terminus occurs, for 2 Pi space: 1/2 diagonal X 1.33.”
Though it seems the term “inverse distance law” should perhaps replace “inverse square law”
. Revboden's formula specifies a distance from the mouth, but would not be dependent on flare rate or frequency.
Revboden’s formula matches what I have been measuring in the real world of bass horns (and front loaded cabinets) for the last forty years.
High horns are subject to air attenuation in addition to the inverse distance law.
Everything from the sources revboden quotes in #304 seem to lock in with what I wrote in #299, where I wrote:
If the cabinet radiating area or array size gets to be significant relative to the measurement distance, there will be a deviation from the inverse square law, as the inverse square law assumes a single point source, which no loudspeaker actually is.
That’s what I’m saying
.Art Welter
revboden wrote:
“The inverse square loss starts just outside the box where the horn's terminus occurs, for 2 Pi space: 1/2 diagonal X 1.33.”
Though it seems the term “inverse distance law” should perhaps replace “inverse square law”
Art Welter
I was referring to sound intensity (IL) not sound pressure (SPL)
for (IL) In free field, intensity varies as 1/r^2
for (SPL) In free field, pressure varies as 1/r
The ideas revboden is expressing apply to free-field radiation in anechoic space. In his links, there are also some discussions of how the reverberent field modifies the energy/distance ratios because the energy is reflected back inside rooms.
But this is an entirely different discussion than what goes on inside a horn.
A horn presents boundary conditions for the wavefront expansion, and actually changes the shape of that expansion. The walls of a horn aren't reflectors in the same sense as they are in a room.
The wavefront that travels down a horn is normal (perpendicular) to the bounding surface. What this means is the curvature of the wavefront is determined by the shape of the horn. The area expansion that gives a horn its impedance transformation also literally curves the wavefront. The cross-section of the horn forms a pie-slice that defines the radiating angle. So it is already developing an expanding wavefront before it even leaves the horn.
The speaker is a vibrating piston, which creates a plane wave. When this plane wave enters the throat, it begins to expand at a rate determined by the flare angle. The walls of the flare are normal to the wavefront, literally curving the wavefront into a spherical wave. As the sperical wave progresses down the horn, it has already begun to be attenuated by its expansion.
At the horn throat, pressure is highest, and it is gradually reduced as the wavefront travels down the horn. In fact, in a conical horn, the pressure attenuation down the horn is precisely the same as a spherical wave in free-space, exactly following the inverse-square law, being a drop of 6dB for every doubling of axial distance traveled down the horn. So you can easily see that the acoustic center of a conical horn is pretty much where the radiating diaphragm is.
To be a little more specific, the acoustic center is where the planar wave from the radiating piston transforms into a spherical wavefront. In a conical horn, this happens at the throat. In a quadratic or catenary (OS) horn, it happens very nearly at the throat, where the curvature bends the wave from planar to spherical. In most other horns, it happens within the horn path, usually near to the throat in a properly sized horn.
In practice, there are lots of other things that come into play. The acoustic center actually moves down the horn towards the mouth as frequency drops, but less so in a full size horn. The flare profile of the horn, its length and mouth area, all have an affect. The acoustic center is a moving target, one that moves with frequency and boundary conditions (nearby walls, groups of horns, etc). But the point is, the acoustic center of a horn is rarely at the mouth. It is almost always somewhere down the throat.
For reference, see the following acoustics textbook:
But this is an entirely different discussion than what goes on inside a horn.
A horn presents boundary conditions for the wavefront expansion, and actually changes the shape of that expansion. The walls of a horn aren't reflectors in the same sense as they are in a room.
The wavefront that travels down a horn is normal (perpendicular) to the bounding surface. What this means is the curvature of the wavefront is determined by the shape of the horn. The area expansion that gives a horn its impedance transformation also literally curves the wavefront. The cross-section of the horn forms a pie-slice that defines the radiating angle. So it is already developing an expanding wavefront before it even leaves the horn.
The speaker is a vibrating piston, which creates a plane wave. When this plane wave enters the throat, it begins to expand at a rate determined by the flare angle. The walls of the flare are normal to the wavefront, literally curving the wavefront into a spherical wave. As the sperical wave progresses down the horn, it has already begun to be attenuated by its expansion.
At the horn throat, pressure is highest, and it is gradually reduced as the wavefront travels down the horn. In fact, in a conical horn, the pressure attenuation down the horn is precisely the same as a spherical wave in free-space, exactly following the inverse-square law, being a drop of 6dB for every doubling of axial distance traveled down the horn. So you can easily see that the acoustic center of a conical horn is pretty much where the radiating diaphragm is.
To be a little more specific, the acoustic center is where the planar wave from the radiating piston transforms into a spherical wavefront. In a conical horn, this happens at the throat. In a quadratic or catenary (OS) horn, it happens very nearly at the throat, where the curvature bends the wave from planar to spherical. In most other horns, it happens within the horn path, usually near to the throat in a properly sized horn.
In practice, there are lots of other things that come into play. The acoustic center actually moves down the horn towards the mouth as frequency drops, but less so in a full size horn. The flare profile of the horn, its length and mouth area, all have an affect. The acoustic center is a moving target, one that moves with frequency and boundary conditions (nearby walls, groups of horns, etc). But the point is, the acoustic center of a horn is rarely at the mouth. It is almost always somewhere down the throat.
For reference, see the following acoustics textbook:
- Sound system engineering (Third Edition), by Don Davis and Eugene Patronis (2006)
I just noticed a way to see previews of the book I just mentioned. Click the link on my last post to go to that book, and then where it says "Search Inside", enter "horn pressure". See pages 277 onward:
Or just click here:
"The pressure attenuation in the horn is the same as that for a spherical wave in free space being a drop of 6dB for each doubling of distance traveled in the horn."
Or just click here:
- Find "Horn pressure" in the preview of Sound system engineering, by Don Davis and Eugene Patronis
"The pressure attenuation in the horn is the same as that for a spherical wave in free space being a drop of 6dB for each doubling of distance traveled in the horn."
I've highlighted two parts of your post, as I think this may be the key point of the whole disagreement between you and Art.
You're saying the acoustic source is near the driver (exactly at the driver in the conical case) in "a properly sized horn" by which I take it you mean an un-compromised horn.
Art is saying that the acoustic centre of the actual bass horns he's measured (individual and pairs?) is near the mouth. Neither of those two statements are necessarily contradictory, because a single bass horn even as large as a 12pi (let alone a smaller one) is a compromised horn when used by itself, as you yourself have already said.
An un-compromised horn behaves as a horn and follows horn theory, a compromised horn is something else entirely and behaves differently, although technically there is a whole range of in between behaviour as the size or frequency transitions you from one to the other. But the point is, once a horn is sufficiently compromised by either having a mouth that's significantly too small or being operated too low in frequency, it's no longer a horn. Eventually it reaches a point where it's just a recessed driver on a baffle.
You are discussing primarily the behaviour of un-compromised horns, whilst Art seems to be basing his discussion on measurements of what must be compromised horns.
I think it's pretty clear to me after reading everything that's been said by both sides that when a horn is acting as a true horn - eg above it's lower cut-off frequency in its un-compromised range, the acoustic centre is near the driver, for the reasons you explain.
When it's being operated a long way below it's horn cut-off frequency (which must surely be the case at the low frequency end for a single bass horn 12pi or smaller in size) then the effective acoustic centre moves forward, because most of the wavefront expansion is now occurring at the mouth, as the mouth is too small to control the wave expansion after it exits the mouth.
In between the two extremes there may be a messy transition region where the acoustic centre doesn't necessarily move from one extreme to the other smoothly and monotonically, and there may be problems with diffraction from the edge of the mouth where the frequency is low enough to spread out around the mouth edge, but still high enough to diffract. I don't know enough about the theory to know whether this happens, but it seems at least plausible.
Last edited:
You're exactly right about the movement of the acoustic center in a horn, and the conditions that make it change and move. It would not be right to assume it to be the mouth. Nor would it be right to assume it's the voice coil, for that matter. That's actually the point - the acoustic center is not a position that is obvious just by looking at a speaker cabinet.
About the "disagreement" - I think it is most decorous of you to see it this way. And I suppose you could be right. But I have a hard time believing that by pure coincidence, all the cabinets measured had their acoustic sources at the front face. This is highly unlikely.
Almost no cabinet has its acoustic center at the front face, even direct radiators. The acoustic center is usually some distance behind the woofer in a front loaded cabinet. In a horn, it is usually somewhere in the throat. It also moves with frequency.
The point of all this should not go wasted in a meandering thread that leaves readers wondering. The point is that the acoustic center is ambiguous unless precisely measured, but path-lenth/acoustic-center error can be mitigated by measuring at a distance.
Honestly, I have a very hard time believing that Art measured several cabinets and always found the 1M SPL values to be the same as the 10M values scaled 20dB. I think what is more likely, is that the 1M values didn't square with his expectations, so he manipulated the drive voltage or the microphone position to make it match. I have said that I thought it was calibration or equipment, but what I actually think is more likely is that he knew his equipment didn't have the accuracy, so he modified the conditions of the test to match what his expected results, in an attempt to make the test seem more accurate.
About the "disagreement" - I think it is most decorous of you to see it this way. And I suppose you could be right. But I have a hard time believing that by pure coincidence, all the cabinets measured had their acoustic sources at the front face. This is highly unlikely.
Almost no cabinet has its acoustic center at the front face, even direct radiators. The acoustic center is usually some distance behind the woofer in a front loaded cabinet. In a horn, it is usually somewhere in the throat. It also moves with frequency.
The point of all this should not go wasted in a meandering thread that leaves readers wondering. The point is that the acoustic center is ambiguous unless precisely measured, but path-lenth/acoustic-center error can be mitigated by measuring at a distance.
Honestly, I have a very hard time believing that Art measured several cabinets and always found the 1M SPL values to be the same as the 10M values scaled 20dB. I think what is more likely, is that the 1M values didn't square with his expectations, so he manipulated the drive voltage or the microphone position to make it match. I have said that I thought it was calibration or equipment, but what I actually think is more likely is that he knew his equipment didn't have the accuracy, so he modified the conditions of the test to match what his expected results, in an attempt to make the test seem more accurate.
Last edited:
Hi Guys
If acoustics was simple, this wouldn’t be a question would it?
There are several things when enter into this issue, the first used to be called the “Rathe” effect but I am not sure what it’s called now.
Picture a tiny 10W projector lamp out in the open. As you walk closer with a light meter, you observe it follows the inverse square law until you are very very close. Conversely, picture an 8 foot square light panel that is evenly illuminated and also radiating the same total photons.
Both radiate the same total energy yet the inverse square law falls apart as you get closer, the intensity does not continue to increase as predicted.
In this case, one can see that when you are very close to the tiny bulb, the distance to the source is a fixed value but as you approach the panel, the intensity increases much more slowly because the source is dispersed physically, when the light meter is touching the panel, some of the source is still “far away” and so is not as intense.
A line array uses the same dispersed source effect (with even larger acoustic spacing) to produce the famous reduced fall off (when it is present) relative to the point source.
For a large pile of horn subs, one can run into the same effect, a measurement at one meter of a physically large source like this will read low relative to what would be ascertained by measuring at a larger distance and is why many have erroneously said bass horns have more “throw”.
They don’t have more throw but the spl can increase more slowly as one approaches and is less intense up close relative to the same acoustic power radiated from a single point.
For a large speaker, the box can occupy some of the 1 meter radius and then in that case, causes an error in the “too high” direction.
A friend that does many of our spherical measurements at work has written a nice blurb on how this effects the higher frequency measurements as well.
http://www.etcinc.us/tech/nl043_far_field_criteria.pdf
http://www.proavmagazine.com/Images/CHEAT1207_tcm46-366821.pdf
So, one can argue that the “origin” is the point where the inverse square law says it is relative to the far distance measurements, or one might say it is where an ETC measurement says it is in time/distance but unless the source is small relative to the source size, the two will be different.
Alternately, as Pat does, one can measure far enough away to avoid these issues and get numbers which are usable to accurately predict SPL at other large distances.
Best,
Tom Danley
If acoustics was simple, this wouldn’t be a question would it?
There are several things when enter into this issue, the first used to be called the “Rathe” effect but I am not sure what it’s called now.
Picture a tiny 10W projector lamp out in the open. As you walk closer with a light meter, you observe it follows the inverse square law until you are very very close. Conversely, picture an 8 foot square light panel that is evenly illuminated and also radiating the same total photons.
Both radiate the same total energy yet the inverse square law falls apart as you get closer, the intensity does not continue to increase as predicted.
In this case, one can see that when you are very close to the tiny bulb, the distance to the source is a fixed value but as you approach the panel, the intensity increases much more slowly because the source is dispersed physically, when the light meter is touching the panel, some of the source is still “far away” and so is not as intense.
A line array uses the same dispersed source effect (with even larger acoustic spacing) to produce the famous reduced fall off (when it is present) relative to the point source.
For a large pile of horn subs, one can run into the same effect, a measurement at one meter of a physically large source like this will read low relative to what would be ascertained by measuring at a larger distance and is why many have erroneously said bass horns have more “throw”.
They don’t have more throw but the spl can increase more slowly as one approaches and is less intense up close relative to the same acoustic power radiated from a single point.
For a large speaker, the box can occupy some of the 1 meter radius and then in that case, causes an error in the “too high” direction.
A friend that does many of our spherical measurements at work has written a nice blurb on how this effects the higher frequency measurements as well.
http://www.etcinc.us/tech/nl043_far_field_criteria.pdf
http://www.proavmagazine.com/Images/CHEAT1207_tcm46-366821.pdf
So, one can argue that the “origin” is the point where the inverse square law says it is relative to the far distance measurements, or one might say it is where an ETC measurement says it is in time/distance but unless the source is small relative to the source size, the two will be different.
Alternately, as Pat does, one can measure far enough away to avoid these issues and get numbers which are usable to accurately predict SPL at other large distances.
Best,
Tom Danley
Agreed. We actually were discussing this a couple days ago. There are some good references a few pages back in this thread.
There are two definitions of the acoustic source, and a discussion of the differences (both academically and in measurement) are shown discussed in the note referenced below.
The two definitions of the acoustic center are:
1. The position from which outgoing wavefronts appear to diverge in the far field, and
2. The position from which the sound pressure varies inversely as the distance
The first definition is primarily concerned with phase, and the second is primarily concerned with amplitude. Both are important.
The phase definition is shown mostly in the path length and is why we have to delay the mains to match the subs. There are also electro-mechanico-acoustic parameters that affect phase, i.e. driver parameters, cabinet shape, configuration, etc. The amplitude definition includes both path length and radiator size. It is the position where the sound source begins to act as a point source, and so it is influenced by both the the path length and the radiating area. There is expansion of the wave within the horn, it is a developing wavefront.
The acoustic source position is really kind of complex. It can be measured, and then a very precise microphone-to-DUT distance can be setup. But another solution presents itself, which is to simply make the measuring distance greater, which then reduces the acoustic-center/path-length error. This makes the SPL measurement more accurate even when the acoustic center position is only approximated, i.e. using the cabinet front as the radiator position and the microphone tip as the receiver position.
Take the 2226, for example. It's a great woofer, I like it a lot. Run it at say 60Hz, with 1 watt input. Stand back several feet and it's pretty loud, but you can talk over it if you talk loudly. Now walk up very close to it, say within a foot. Now it's really loud. You can't talk over it anymore, you'd definitely have to shout.
Do the same thing with a basshorn. As much as I like the 2226, a good basshorn will be 10dB louder. You will notice that loudness when you stand several feet back, but now walk up close, right up next to the mouth. It doesn't seem as loud one foot away from the face as the direct radiating 2226 did. In fact, it isn't as loud. This is because its acoustic center is some ten feet further back.
There are two definitions of the acoustic source, and a discussion of the differences (both academically and in measurement) are shown discussed in the note referenced below.
The two definitions of the acoustic center are:
1. The position from which outgoing wavefronts appear to diverge in the far field, and
2. The position from which the sound pressure varies inversely as the distance
The first definition is primarily concerned with phase, and the second is primarily concerned with amplitude. Both are important.
The phase definition is shown mostly in the path length and is why we have to delay the mains to match the subs. There are also electro-mechanico-acoustic parameters that affect phase, i.e. driver parameters, cabinet shape, configuration, etc. The amplitude definition includes both path length and radiator size. It is the position where the sound source begins to act as a point source, and so it is influenced by both the the path length and the radiating area. There is expansion of the wave within the horn, it is a developing wavefront.
The acoustic source position is really kind of complex. It can be measured, and then a very precise microphone-to-DUT distance can be setup. But another solution presents itself, which is to simply make the measuring distance greater, which then reduces the acoustic-center/path-length error. This makes the SPL measurement more accurate even when the acoustic center position is only approximated, i.e. using the cabinet front as the radiator position and the microphone tip as the receiver position.
- A note on the concept of acoustic center, by Jacobsen, Figueroa and Rasmussen
Take the 2226, for example. It's a great woofer, I like it a lot. Run it at say 60Hz, with 1 watt input. Stand back several feet and it's pretty loud, but you can talk over it if you talk loudly. Now walk up very close to it, say within a foot. Now it's really loud. You can't talk over it anymore, you'd definitely have to shout.
Do the same thing with a basshorn. As much as I like the 2226, a good basshorn will be 10dB louder. You will notice that loudness when you stand several feet back, but now walk up close, right up next to the mouth. It doesn't seem as loud one foot away from the face as the direct radiating 2226 did. In fact, it isn't as loud. This is because its acoustic center is some ten feet further back.
Idea: two different Acoustic Centers (AC) (defined as point of phase alignment) one inside the horn length and one outside the mouth. the two points being 180deg. from each other. when the internal point moves down the mouth and aligns with the external AC, phase cancellation occurs (around 110-120hz in most cases) but when the horns are coupled together in an array and the external AC is further away from the mouth, the Internal AC and the external AC cannot align. thus the null seen with one box is not present in arrays.
wayne, you wrote
"Do the same thing with a basshorn. As much as I like the 2226, a good basshorn will be 10dB louder. You will notice that loudness when you stand several feet back, but now walk up close, right up next to the mouth. It doesn't seem as loud one foot away from the face as the direct radiating 2226 did. In fact, it isn't as loud. This is because its acoustic center is some ten feet further back."
Could it be that several feet back is the external acoustic center and you just walked through it. and if you stuck your head inside the horn you would find another convergence point?
wayne, you wrote
"Do the same thing with a basshorn. As much as I like the 2226, a good basshorn will be 10dB louder. You will notice that loudness when you stand several feet back, but now walk up close, right up next to the mouth. It doesn't seem as loud one foot away from the face as the direct radiating 2226 did. In fact, it isn't as loud. This is because its acoustic center is some ten feet further back."
Could it be that several feet back is the external acoustic center and you just walked through it. and if you stuck your head inside the horn you would find another convergence point?
Wayne,
The phenomenon you mention simply has to do with the area of the radiating surface, and nothing to do with the depth of the horn.
A bass horn with a 45 x 28 inch mouth has a radiating area of 1260 square inches, while a 15 inch speaker has only 135 square inches of radiating area. The bass horn has more than nine times the radiating area, obviously if the two are played at the same SPL ”several feet back” then move the dB meter to the horn mouth, it will read lower at the horn mouth than an inch from the 15 inch speaker.
The same effect would occur if you placed nine 15 inch speakers on a baffle and compared it to one 15 at the same SPL at one meter, then moved the meter or your ear an inch from the center of the nine, the center of the single 15 will be much louder.
In each case the inverse distance law will prevail outside of the immediate near field of the radiating surface, the SPL level in a half space will drop at 6.02 dB per doubling of distance.
In #216. You wrote:
“Also, as I said, if you don't measure at a distance the measurements cannot be compared. In a true horn, the source is further away than it is in a tapped horn/pipe. The difference in source distance is significant, given the inverse-square law. “
My response in post #218 showed your postulation to be incorrect.
Phil Lewandowski’s test results, done under good outdoor conditions free of reflective objects, prove without doubt your postulation is incorrect, all his tests are within a dB of the 30.1 dB drop the inverse distance law predicts.
In post #312, you wrote:
“Honestly, I have a very hard time believing that Art measured several cabinets and always found the 1M SPL values to be the same as the 10M values scaled 20 dB. I think what is more likely, is that the 1M values didn't square with his expectations, so he manipulated the drive voltage or the microphone position to make it match. I have said that I thought it was calibration or equipment, but what I actually think is more likely is that he knew his equipment didn't have the accuracy, so he modified the conditions of the test to match what his expected results, in an attempt to make the test seem more accurate.”
My test was done on May 15, 2010, in response to a question raised by Harry Brill Jr. the day before,
with a speculation similar to what you wrote in #216.
I decided to do an actual test since his question had never been answered to my satisfaction in any text book, though the postulation has been bandied about as long as I can remember.
My test readings were in no way manipulated, though they were obviously influenced from 2-8 meters by the locations of buildings.
I did the test in the morning, wrote up the results, posted them, and left for a gig.
The tests were all done starting at 110 dBC at one meter, which required resetting the output level for each cabinet, then moving the dB meter to speaker cutouts (round plywood discs) placed at 1,2,4,8,16,and 32 meters.
That test showed the horn sub dropped 32 dB at 50 Hz and 30 dB at 125 Hz from 1-32 meters.
If you average those two numbers the difference is less than one dB from predicted.
You accused me of manipulating drive voltage or the microphone positions, I challenge you to do the inverse distance test yourself, you will find that the path length of a horn with a mouth size of around one square meter or less does not deviate from the inverse distance law from 1-32 meters.
Repeat the test, put the issue to rest.
Art Welter
Attachments
Tom,
It's still called "Rathe effect'
ref: ScienceDirect - Journal of Sound and Vibration : Method of predicting Leq created by urban traffic
Rathe has shown that for a building of elevation dimensions a and b the building will behave as an area source until the distance d from the building > a/π or b/π and then as a linear source until a/π and b/π < d after which a point source can be assumed.
It's still called "Rathe effect'
ref: ScienceDirect - Journal of Sound and Vibration : Method of predicting Leq created by urban traffic
Rathe has shown that for a building of elevation dimensions a and b the building will behave as an area source until the distance d from the building > a/π or b/π and then as a linear source until a/π and b/π < d after which a point source can be assumed.
That does not square with basic acoustic texts, or with measured results. There are a lot of things that affect the position of the acoustic center, and in the case of a horn, path length is one of them.
At the apex of a horn, there is a vibrating piston (the diaphragm or cone), which creates a plane wave. When this plane wave enters the throat, it begins to expand at a rate determined by the flare angle. The walls of the flare are normal to the wavefront, literally curving the wavefront into a spherical wave. As the sperical wave progresses down the horn, it has already begun to be attenuated by its expansion.
At the horn throat, pressure is highest, and it is gradually reduced as the wavefront travels down the horn. In fact, in a conical horn, the pressure attenuation down the horn is precisely the same as a spherical wave in free-space, exactly following the inverse-square law, being a drop of 6dB for every doubling of axial distance traveled down the horn. So you can easily see that the acoustic center of a conical horn is pretty much where the radiating diaphragm is.
To be a little more specific, the acoustic center is where the planar wave from the radiating piston transforms into a spherical wavefront. In a conical horn, this happens at the throat. In a quadratic or catenary (OS) horn, it happens very nearly at the throat, where the curvature bends the wave from planar to spherical. In most other horns, it happens within the horn path, usually near to the throat in a properly sized horn.
In practice, there are lots of other things that come into play. The acoustic center actually moves down the horn towards the mouth as frequency drops, but less so in a full size horn. The flare profile of the horn, its length and mouth area, all have an affect. The acoustic center is a moving target, one that moves with frequency and boundary conditions (nearby walls, groups of horns, etc). But the point is, the acoustic center of a horn is rarely at the mouth. It is almost always somewhere down the throat.
For reference, see the following acoustics textbook:
- Sound system engineering (Third Edition), by Don Davis and Eugene Patronis (2006)
Last edited:
Quote:
Originally Posted by Wayne Parham
Take the 2226, for example. It's a great woofer, I like it a lot. Run it at say 60Hz, with 1 watt input. Stand back several feet and it's pretty loud, but you can talk over it if you talk loudly. Now walk up very close to it, say within a foot. Now it's really loud. You can't talk over it anymore, you'd definitely have to shout.
Do the same thing with a basshorn. As much as I like the 2226, a good basshorn will be 10dB louder. You will notice that loudness when you stand several feet back, but now walk up close, right up next to the mouth. It doesn't seem as loud one foot away from the face as the direct radiating 2226 did. In fact, it isn't as loud. This is because its acoustic center is some ten feet further back.
Quote:
Originally Posted by weltersys
Wayne,
The phenomenon you mention simply has to do with the area of the radiating surface, and nothing to do with the depth of the horn.
A bass horn with a 45 x 28 inch mouth has a radiating area of 1260 square inches, while a 15 inch speaker has only 135 square inches of radiating area. The bass horn has more than nine times the radiating area, obviously if the two are played at the same SPL ”several feet back” then move the dB meter to the horn mouth, it will read lower at the horn mouth than an inch from the 15 inch speaker.
The same effect would occur if you placed nine 15 inch speakers on a baffle and compared it to one 15 at the same SPL at one meter, then moved the meter or your ear an inch from the center of the nine, the center of the single 15 will be much louder.
In each case the inverse distance law will prevail outside of the immediate near field of the radiating surface, the SPL level in a half space will drop at 6.02 dB per doubling of distance.
You have been unable to provide any actual data showing a horn sub of one square meter or less mouth area that does not conform to the inverse distance law as measured from 1 to 32 meters.
There is a simple reason for that lack of data on your part, subs of one square meter or less mouth area conform to the inverse distance law as measured from 1 to 32 meters.
Art Welter
Originally Posted by Wayne Parham
Take the 2226, for example. It's a great woofer, I like it a lot. Run it at say 60Hz, with 1 watt input. Stand back several feet and it's pretty loud, but you can talk over it if you talk loudly. Now walk up very close to it, say within a foot. Now it's really loud. You can't talk over it anymore, you'd definitely have to shout.
Do the same thing with a basshorn. As much as I like the 2226, a good basshorn will be 10dB louder. You will notice that loudness when you stand several feet back, but now walk up close, right up next to the mouth. It doesn't seem as loud one foot away from the face as the direct radiating 2226 did. In fact, it isn't as loud. This is because its acoustic center is some ten feet further back.
Quote:
Originally Posted by weltersys
Wayne,
The phenomenon you mention simply has to do with the area of the radiating surface, and nothing to do with the depth of the horn.
A bass horn with a 45 x 28 inch mouth has a radiating area of 1260 square inches, while a 15 inch speaker has only 135 square inches of radiating area. The bass horn has more than nine times the radiating area, obviously if the two are played at the same SPL ”several feet back” then move the dB meter to the horn mouth, it will read lower at the horn mouth than an inch from the 15 inch speaker.
The same effect would occur if you placed nine 15 inch speakers on a baffle and compared it to one 15 at the same SPL at one meter, then moved the meter or your ear an inch from the center of the nine, the center of the single 15 will be much louder.
In each case the inverse distance law will prevail outside of the immediate near field of the radiating surface, the SPL level in a half space will drop at 6.02 dB per doubling of distance.
My statements are based on measured test results that have specifically been done to measure horn loaded compared to front loaded cabinets showing that cabinets in the size range of what have been discussed in this thread, with differing acoustic origin distance, with frontal area around one meter or less, when tested in one or two units, conform to the inverse square law as measured from 1 to 32 meters from the cabinet front, not some distance emanating from within the cabinet.
You have been unable to provide any actual data showing a horn sub of one square meter or less mouth area that does not conform to the inverse distance law as measured from 1 to 32 meters.
There is a simple reason for that lack of data on your part, subs of one square meter or less mouth area conform to the inverse distance law as measured from 1 to 32 meters.
Art Welter
Isn't this exactly what I've been saying for the last couple of days ? That as you get too close to an acoustically large source the SPL won't increase as much as expected since you're in the near field, and the measurement will be in error such that it can't be extrapolated into the far field.
The first link posted by Tom Danley spells all this out in excellent detail as well as a number of bounding conditions that need to be satisfied to be sure you're within the far-field of a given speaker at the frequencies you're measuring at.
A useful rule of thumb given in the article for low frequencies is that you want to be at least 3 times the largest active dimension of the speaker away to ensure that you're not in the near-field. Funnily enough I've already come across this rule of thumb a long time ago, (although expressed as 6 times the driver radius) and try as much as possible to stick to it.
By this rule of thumb a bass horn with a ~1 metre tall mouth such as the 12pi shouldn't be measured any closer than ~3 metres if you want to be able to accurately extrapolate the data to greater distances, regardless of whether the acoustic centre source depth is known accurately or not.
By this same rule of thumb the absolute largest driver you could measure at 1 metre and still be able to extrapolate the SPL data at a distance accurately (or compare accurately to another speaker of largely differing size) is a 15" woofer, whose active cone diameter is a little over 30cm.
Yet you stated further back in the thread that you see no problem with taking a measurement at 1 metre from a bass horn that has a 1 metre wide or high mouth - something that violates this 3 to 1 rule by a factor of three.
It's convenient of you to just average the two results and say "look, it's 1dB away from inverse square law fall off". Did it occur that the cause of the 2dB difference in fall off between 50Hz and 125Hz on the horn might be a result of the acoustic centre of the horn shifting with frequency ?
At 50Hz one horn by itself is very likely compromised, bringing the acoustic centre forward somewhat, while at 125Hz it will be a lot closer to being un-compromised and pushing the acoustic centre back towards the driver.
If the acoustic centre was further forward at 50Hz, you would expect more total fall off from near to far, because you're going from ~1 metre to ~32 metres, whilst at 125Hz you're going from maybe ~1.5 metres to ~32.5 metres with the same microphone locations. This is consistent with the 2dB difference, and in the right direction, however its probably within the error margin of the measurements.
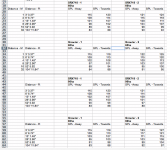
I think it's helpful to look at graphs rather than raw numbers to see what's really going on and whether the measurements deviate or not, so I took the liberty of putting your measurements into an excel spreadsheet and graphing them, which I've attached as two images.
The yellow line is the predicted theoretical inverse square law fall off. The first graph has a linear distance axis while the second has a logarithmic distance axis, which is convenient because it makes inverse square law fall off a straight line, making it easier to see how the measurements deviate from the predicted response.
There is a huge periodic wiggle in the readings between 2 and 8 metres, presumably from a building reflection. The magnitude of the deviations is far greater than the small difference we're trying to measure which is probably only on the order of 2dB or so. Even at 32 metres the slope of the lines have not converged at the correct inverse square law fall off on 3 of the 4 measurements.
The fact that the horn at 125Hz follows most closely with the predicted response suggests that the directivity of the horn at that frequency is reducing the magnitude of some off axis reflection.
The inescapable conclusion is that there is far too much experimental error in the measurements (probably reflections) to provide any meaningful confirmation or denial of the facts being argued over. I have to agree with Wayne that your measurements in this particular instance don't prove anything one way or the other.
Attachments
Last edited:
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.