Think of it this way- the energy coming into the coil gives it an acceleration, more voltage ramps it up, but at higher frequencies the direction of travel reverses sooner than at lower frequencies, hence less travel. With a thousand times more time, that pipe organ bass note moves the diaphragm a whole lot more in each direction than your 20k shimmer of a brush on a cymbal.
This is what I'm wondering, so, the speaker isn't fast enough to attain full excursion at higher frequencies, luckily for flat FR (SPL) this isn't necessary 🙂. The OPs question is an interesting one that isn't easy to answer.....
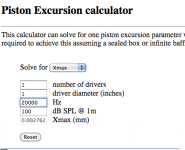
When you punch in the numbers to that calculator it shows that every octave you rise, requires 1/4x excursion
It's not that it is not fast enough, the principle would not change with an infinitely light diaphragm. It's spending less time moving forward, thus going less far. I'm afraid I should not have used accelerate instead of maybe impel or propel. Sorry.
simple physics approximation would use BL force product and moving mass to get accel/Ampere, pick a Amp limit from coil R and power spec
then x_ peak should be BL*A_pk / (vc_mass * w^2), w = radian frequency
wasted all the time before dinner looking for a units package in Python, numbers later
then x_ peak should be BL*A_pk / (vc_mass * w^2), w = radian frequency
wasted all the time before dinner looking for a units package in Python, numbers later
Last edited:
~ 0.0002" for the ScanSpeak Revelator 1" numbers? (+/- a spherical cow)
of course a soft dome doesn't move as a single mass @20 kHz, but we could pretend, or look for Accuton numbers
so the next question is how many continuous A @20 kHz if the 225 W spec was believable
sympy v 1.1.1
of course a soft dome doesn't move as a single mass @20 kHz, but we could pretend, or look for Accuton numbers
so the next question is how many continuous A @20 kHz if the 225 W spec was believable
sympy v 1.1.1
Last edited:
Well having resolved that problem, one only has to ask ....how many bacteria can live on the head of a pin ?
C.M
C.M
Mmm, I don't quite get that, doesn't that imply the same thing, ie, it's not fast enough to realise the full peak to peak signal?
I thought that for the same SPL the extension was inversely proportional to the frequency.
i.e. double the frequency results in half the excursion.
If that is true and the treble unit has 0.5mm Xmax for use at 2kHz, then @ 20kHz it would be using only 0.05mm of excursion for the same SPL.
This would fit with CalW's 0.05mm inspired guess.
Last edited:
Doubling the frequency means a quarter of the excursion for the same SPL. I was wrong to use the term frequency response, I was thinking of the peak to peak signal being reproduced linearly by the voice coil
Nothing as exciting as the neighbor's dog -- I just need to set up a simple experiment to compress and rarefy the air in a small chamber that has a very small "port". I want to minimize audible noise; hence, the high frequency.
1" direct radiator tweeters may not be too useful - check out the sound wavelength compared to your 'small chamber' dimensions
20 kHz 1/4 wave is ~ 0.16", above that and you are getting transmisson line effects, reflections, standing waves...
look at compression drivers - the phase plug is needed to get even ~ flat (or spherical cap) wavefront across the opening
20 kHz 1/4 wave is ~ 0.16", above that and you are getting transmisson line effects, reflections, standing waves...
look at compression drivers - the phase plug is needed to get even ~ flat (or spherical cap) wavefront across the opening
If you go with a metal dome tweeter, especially a cheap one, it will have a savage resonance somewhere between 24KHz and 30kHz if you tune to this frequency you will get much more acoustic output for the electrical energy input. Also if this experiment is for children you need to get above 22KHz or some of them might be able to hear it.
- Status
- Not open for further replies.