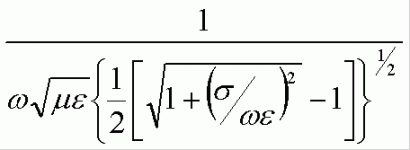SY,
Yes, there are a few assumptions, one, that the conductor is homogeneous, meaning having the same conductivity throughout and that the length is large wrt the diameter, two that the freq is high enough that the skin effect is pronounced. With lower freq and/or smaller diameters it gets more gradual as you say. In fact, as far as I know, the full equation is a bessel function with a complex argument. I'm not sure I know what that means, let alone that I know what it means ....
However, delta is interesting in that the ratio of Rac/Rdc of the conductor at the radian freq omega = (a/2*delta)+0.25 (where a is the diameter of the conductor).
Still, it is amusing to see that after a long silence, now that one person gives a solution, hordes of others come running to improve on that.
Jan Didden
Yes, there are a few assumptions, one, that the conductor is homogeneous, meaning having the same conductivity throughout and that the length is large wrt the diameter, two that the freq is high enough that the skin effect is pronounced. With lower freq and/or smaller diameters it gets more gradual as you say. In fact, as far as I know, the full equation is a bessel function with a complex argument. I'm not sure I know what that means, let alone that I know what it means ....
However, delta is interesting in that the ratio of Rac/Rdc of the conductor at the radian freq omega = (a/2*delta)+0.25 (where a is the diameter of the conductor).
Still, it is amusing to see that after a long silence, now that one person gives a solution, hordes of others come running to improve on that.
Jan Didden
Re: skin depth
It seems I have to apologize to Richard, he posted the equation way before me, I missed it. Sorry Richard!
I also realise why my equation has no sigma: the assumtion here was that sigma (conductivity) >> omega*epsilon (epsilon being the materials' dielectric constant). Do you agree SY?
Jan Didden
1/137 said:
It seems I have to apologize to Richard, he posted the equation way before me, I missed it. Sorry Richard!
I also realise why my equation has no sigma: the assumtion here was that sigma (conductivity) >> omega*epsilon (epsilon being the materials' dielectric constant). Do you agree SY?
Jan Didden
Effects of epsilon
Well, I don't mean to turn this into a contest, but 1/137 asked about epsilon. I dug up the equation for skin depth that includes the effect of epsilon and tried it out with the equation editor from Word XP. The equation editor is not too bad! The equation previously posted assumes a good conductor, so epsilon drops out. The equation below doesn't make that assumption. I got this from from "Advanced Engineering Electromagnetics" by Balanis, page 149.
As is the case for the other equations previously posted, this is for a TEM mode plane wave, which is different from what you'll get in a transmission line application with lossy conductors. I don't have a clue as to how the transmission line problem is solved with a lossy conductor and a uniform cross-section, let alone when twisting gets into the picture. For sure the propagation is no longer TEM mode, and that really complicates things.
Well, I don't mean to turn this into a contest, but 1/137 asked about epsilon. I dug up the equation for skin depth that includes the effect of epsilon and tried it out with the equation editor from Word XP. The equation editor is not too bad! The equation previously posted assumes a good conductor, so epsilon drops out. The equation below doesn't make that assumption. I got this from from "Advanced Engineering Electromagnetics" by Balanis, page 149.
As is the case for the other equations previously posted, this is for a TEM mode plane wave, which is different from what you'll get in a transmission line application with lossy conductors. I don't have a clue as to how the transmission line problem is solved with a lossy conductor and a uniform cross-section, let alone when twisting gets into the picture. For sure the propagation is no longer TEM mode, and that really complicates things.
Attachments
Andy...
1. i agree...this is NOT a contest...
2. without seeing the derivation i can't say much..but i wonder if there isn't a classical dielectic (as well as a conductor) in the model used to derive that equation.
3. the dielectric onstant for a metal is a complex quantity with the complex part being sigma/omega....based on what i have in front of me.
4. the derivation that yields a simple formula for delta that i posted...(and Jan posted something very similar)....looks at a metal half plane and derives the field strength as a function of depth...and it falls out to be cleanly a function of mu, sigma & omega...which sorta makes sense...at least to me..
time to refill the chardonnay...
SY...any recomendations for someone on a budget...it will be red time soon as it gets cooler.
rt
1. i agree...this is NOT a contest...
2. without seeing the derivation i can't say much..but i wonder if there isn't a classical dielectic (as well as a conductor) in the model used to derive that equation.
3. the dielectric onstant for a metal is a complex quantity with the complex part being sigma/omega....based on what i have in front of me.
4. the derivation that yields a simple formula for delta that i posted...(and Jan posted something very similar)....looks at a metal half plane and derives the field strength as a function of depth...and it falls out to be cleanly a function of mu, sigma & omega...which sorta makes sense...at least to me..
time to refill the chardonnay...
SY...any recomendations for someone on a budget...it will be red time soon as it gets cooler.
rt
Frank: Bare wire is a good approximation, since the conductivity and polarizability are pretty low on the scales we're talking about. As Jan points out, quite correctly.
Jan: That formula was indeed given earlier in the thread, and in about half a dozen other discusions that I can recall. No-one here has solved or found the solution which incorporates the wire geometry for delta of the same order as radius. I hate to sound like I'm harping on that, but a factor of 5 or 6 (or 6.28) isn't out of the question, and that totally changes recommended wire diameters under the (IMO questionable) paradigms put forth by several cable peddlers. Experimentally, I just haven't seen much of an effect with real-world wires within the audio bandwidth.
1/137: I have an inordinate fondness for Côtes-du-Rhône and Loire reds. My bargain red for the moment, though, is J-P Brun's Beaujolais Cuvee Ancienne; earthy, red fruit, and far too easy to drink. The importer can be found at www.louisdressner.com and if you can get mail-order in your state, it can be bought from Chambers Street Wine in NY. If not, the importer (Joe Dressner) might be able to recommend a place in your area. Tell him that I sent you.
Jan: That formula was indeed given earlier in the thread, and in about half a dozen other discusions that I can recall. No-one here has solved or found the solution which incorporates the wire geometry for delta of the same order as radius. I hate to sound like I'm harping on that, but a factor of 5 or 6 (or 6.28) isn't out of the question, and that totally changes recommended wire diameters under the (IMO questionable) paradigms put forth by several cable peddlers. Experimentally, I just haven't seen much of an effect with real-world wires within the audio bandwidth.
1/137: I have an inordinate fondness for Côtes-du-Rhône and Loire reds. My bargain red for the moment, though, is J-P Brun's Beaujolais Cuvee Ancienne; earthy, red fruit, and far too easy to drink. The importer can be found at www.louisdressner.com and if you can get mail-order in your state, it can be bought from Chambers Street Wine in NY. If not, the importer (Joe Dressner) might be able to recommend a place in your area. Tell him that I sent you.
1/137 said:
The derivation proceeds pretty much like what you've described. A TEM-mode plane wave is normally incident on a semi-infinite block of material. So you still have TEM mode propagation inside the material. There's only the classical models of sigma, mu and epsilon used for the material. No complex dielectric constants like what's used to describe dielectric heating of water in microwave ovens and such. The Helmholtz equation in the frequency domain
del squared E = gamma*gamma*E
is used. The propagation constant is given by
gamma*gamma = j*omega*mu*sigma-omega*omega*mu*epsilon
The real part of gamma determines the nepers/meter of attenuation in the material. The skin depth in meters is just the reciprocal of the real part of gamma.
The formula I posted should reduce to what you posted if you make the assumption that (sigma/(omega*epsilon)) >> 1 (I hope!
)
yes it does
Andy,
yes it does indeed reduce but it must be one ugly derivation to end up with that formula when something much simpler contains all the physical content for that situation...
start with del squared A = mu sigma partial A/wrt t add the field + BC do separation of variables and you get the formula for delta...guess this is the difference between a physicist and an engineer...i definitely want to find the book you referenced and look at the derivation...you also might want to look at Jackson as it i suspect it is a lot cleaner from a physical perspective.
rt
Andy,
yes it does indeed reduce but it must be one ugly derivation to end up with that formula when something much simpler contains all the physical content for that situation...
start with del squared A = mu sigma partial A/wrt t add the field + BC do separation of variables and you get the formula for delta...guess this is the difference between a physicist and an engineer...i definitely want to find the book you referenced and look at the derivation...you also might want to look at Jackson as it i suspect it is a lot cleaner from a physical perspective.
rt
Hi,
Fine, so I was on the right track.
Sy, what are the recommended wire diameters? And recommended by whom?
If we're talking about Dr. Malcolm Hawksfords' findings then I tend to agree with those in general in that for all things audio you don't really need thick cables.
He concluded a wire thickness of 0.4 mm would pass all audio frequencies.
What I can't recall from the articles is the "at what current" question though.
From experiments I'd say 0.4mm for anything low level would be more than satisfactory gaugewise.
I run 1mm wire gauge to my speakers in short runs of about 2 meters and can't complain about a lack of lows either.
When you talk about wire geometry do you refer to flat versus round wire and what have you or is this a wire to wire geometry?
Which I'd refer to as cable geometry for clarity's sake anyway.
TIA,
Fine, so I was on the right track.
Sy, what are the recommended wire diameters? And recommended by whom?
If we're talking about Dr. Malcolm Hawksfords' findings then I tend to agree with those in general in that for all things audio you don't really need thick cables.
He concluded a wire thickness of 0.4 mm would pass all audio frequencies.
What I can't recall from the articles is the "at what current" question though.
From experiments I'd say 0.4mm for anything low level would be more than satisfactory gaugewise.
I run 1mm wire gauge to my speakers in short runs of about 2 meters and can't complain about a lack of lows either.
When you talk about wire geometry do you refer to flat versus round wire and what have you or is this a wire to wire geometry?
Which I'd refer to as cable geometry for clarity's sake anyway.
TIA,
Hi,
I remember searching for them when we first discussed this here but couldn't find them on the web.
The paper was published by the British magazine Hifi-News and Record Review back in 1991 or maybe 1992 if memory serves.
It's certainly worth reading but I just haven't kept it, regretably.
One person I can think of who may have a copy is Thorsten Loesch.
Other than that you may have to ask the mag for a copy.
Cheers,
I remember searching for them when we first discussed this here but couldn't find them on the web.
The paper was published by the British magazine Hifi-News and Record Review back in 1991 or maybe 1992 if memory serves.
It's certainly worth reading but I just haven't kept it, regretably.
One person I can think of who may have a copy is Thorsten Loesch.
Other than that you may have to ask the mag for a copy.
Cheers,
Re: yes it does
Hi rt,
The thing I like about the Helmholtz equations as compared to the vector potential approach is that tha propagation constant appears explicitly on the right side after you plug in the exp(j*omega*t) time dependency. Then the skin depth is simply found as the reciprocal of the real part of the propagation constant. So it's just algebra in going from the frequency domain Helmholtz equation to the skin depth.
Regarding the Balanis book, it's my favorite EM theory book. It covers more advanced stuff than undergraduate texts, yet for me it is easier to understand than any of the undergraduate texts I've read. I've heard that Jackson is good as well, but maybe more oriented toward Physics majors, maybe more theoretical? I will check it out for sure.
1/137 said:
Hi rt,
The thing I like about the Helmholtz equations as compared to the vector potential approach is that tha propagation constant appears explicitly on the right side after you plug in the exp(j*omega*t) time dependency. Then the skin depth is simply found as the reciprocal of the real part of the propagation constant. So it's just algebra in going from the frequency domain Helmholtz equation to the skin depth.
Regarding the Balanis book, it's my favorite EM theory book. It covers more advanced stuff than undergraduate texts, yet for me it is easier to understand than any of the undergraduate texts I've read. I've heard that Jackson is good as well, but maybe more oriented toward Physics majors, maybe more theoretical? I will check it out for sure.
Frank: Hawksford, yes, and also Noel Lee. No doubt there are many others: that plane-approximation formula keeps showing up over and over in the tweak community- a fine example of a meme.
If I hadn't refrained from practicing this stuff for the past 20 years or so, I'd dig out Jackson and go solve it myself. But I have, so I can't.
If I hadn't refrained from practicing this stuff for the past 20 years or so, I'd dig out Jackson and go solve it myself. But I have, so I can't.