Here's Huygen's Principle as applied to sound. How does sound move? Wave Propagation and Huygens’ Principle – Discovery of Sound in the Sea
The 'envelope of the wavelets' - that's what it's all about!
The 'envelope of the wavelets' - that's what it's all about!
I'd say the minimum infinite baffle for a driver is one where the wavelengths being demanded (passband) are within <0.25dB (or whatever the listener determines as their auditability threshold) of the maximum theoretical infinite baffle.
OK, ok, folks time out on the wavelets. Let me cough up another hairball's worth of my confusion on this topic, and then we can start the cycle of fun all over again!
So, firstly, there is my question about the "physics". By that I mean the underlying basis for the "wave support" that makes a driver in a very large or semi-infinite baffle have +6dB WRT a more narrow baffle below the baffle step. I think what I am not quite understanding is WHY the support happens at all, since the wave will eventually reach the edge of the baffle and then expand into the larger space. So I guess a more pointed question is, and especially regarding the baffle step frequency, why do we get +6dB if the baffle is not infinite? Phenomenologically speaking I assume it must be something related to getting an entire period of the wave at a particular frequency established/supported on/across the plane of the baffle, and that this is enough to get the +6dB SPL. But I am curious about the exact mechanism by which the wave gets/establishes this support and why 1 wavelength (or whatever the length may be) is enough for that to happen. So that is one part of my rehash of my first post, related to what I brought up about Olson's work.
The next part is about diffraction from very wide baffles, and the idea that Linkwitz put forth, e.g. that for loudspeakers to "disappear" in the room the mind should not be distracted by echoes/reflections that occur before about 6msec after the direct sound arrives. So that I can assign some term to this, let's call it the "forbidden echo period". This concept of a “forbidden echo period” is based on the precedence effect, the hearing process, and what will result in the best performance of the loudspeaker in the room. Linkwitz used it to argue that sidewall reflections, in his narrow listening space, were undesirable and attempted to suppress them by aiming the nulls of his dipole loudspeakers there. But it seems that the baffle size and whether the forbidden echo period is violated (for any type of loudspeaker, not just dipole/OB) are related, since diffraction at an edge creates a new phantom source. For example, I think there is anecdotal evidence that “small” speakers image well and sound good, albeit having a limited bandwidth (limited LF capabilities). The small speaker seems to break SL’s rule because the phantom source will arrive within the forbidden echo period because the edges are "too close" to the source.
When I starting thinking about this in general, I thought of the opposite case: a very large and wide baffle. Diffraction from baffle edges would tend to push the arrival time of the edge diffraction’s phantom source farther out in time, almost ensuring that no diffraction will occur during the forbidden echo period. No diffraction means no additional "source echoes" and that should sound "good". But the anecdotal evidence that I recall for "wide" loudspeakers was that they tended to lack a good soundstage. Put the speaker in the wall and this was even more true (again this is my recollection). And THIS is what I was thinking of when I had the idea to write the OP about "infinite baffles", and when they were and were not infinite for various audio frequencies.
Of course I am also thinking about open baffle loudspeakers, since I am very interested in them, or at least speakers with dipole radiation. But I see a large OB speaker and something of a hybrid. At low frequencies the baffle is too small and front and back sides "see" each other. But as frequency increases, the baffle transitions through and above the baffle step. Even if there is backside radiation, the large baffle is "in the way" of it getting to the listener. Many of these systems use a fullranger, or transition to a dome or horn tweeter that is only front firing. This is obviously not providing any rear-side acoustic output at HF whatsoever. Even when there is rear-side radiation, with a large baffle we are probably above what would be the baffle step for a closed box speaker. Even though the baffle is "open" this HF region seems to be more akin to closed box loudspeaker with a very wide baffle. This has be again thinking about the small vs large size loudspeaker in terms of soundstage, etc. and how this might influence the performance of a large OB type speaker.
So, firstly, there is my question about the "physics". By that I mean the underlying basis for the "wave support" that makes a driver in a very large or semi-infinite baffle have +6dB WRT a more narrow baffle below the baffle step. I think what I am not quite understanding is WHY the support happens at all, since the wave will eventually reach the edge of the baffle and then expand into the larger space. So I guess a more pointed question is, and especially regarding the baffle step frequency, why do we get +6dB if the baffle is not infinite? Phenomenologically speaking I assume it must be something related to getting an entire period of the wave at a particular frequency established/supported on/across the plane of the baffle, and that this is enough to get the +6dB SPL. But I am curious about the exact mechanism by which the wave gets/establishes this support and why 1 wavelength (or whatever the length may be) is enough for that to happen. So that is one part of my rehash of my first post, related to what I brought up about Olson's work.
The next part is about diffraction from very wide baffles, and the idea that Linkwitz put forth, e.g. that for loudspeakers to "disappear" in the room the mind should not be distracted by echoes/reflections that occur before about 6msec after the direct sound arrives. So that I can assign some term to this, let's call it the "forbidden echo period". This concept of a “forbidden echo period” is based on the precedence effect, the hearing process, and what will result in the best performance of the loudspeaker in the room. Linkwitz used it to argue that sidewall reflections, in his narrow listening space, were undesirable and attempted to suppress them by aiming the nulls of his dipole loudspeakers there. But it seems that the baffle size and whether the forbidden echo period is violated (for any type of loudspeaker, not just dipole/OB) are related, since diffraction at an edge creates a new phantom source. For example, I think there is anecdotal evidence that “small” speakers image well and sound good, albeit having a limited bandwidth (limited LF capabilities). The small speaker seems to break SL’s rule because the phantom source will arrive within the forbidden echo period because the edges are "too close" to the source.
When I starting thinking about this in general, I thought of the opposite case: a very large and wide baffle. Diffraction from baffle edges would tend to push the arrival time of the edge diffraction’s phantom source farther out in time, almost ensuring that no diffraction will occur during the forbidden echo period. No diffraction means no additional "source echoes" and that should sound "good". But the anecdotal evidence that I recall for "wide" loudspeakers was that they tended to lack a good soundstage. Put the speaker in the wall and this was even more true (again this is my recollection). And THIS is what I was thinking of when I had the idea to write the OP about "infinite baffles", and when they were and were not infinite for various audio frequencies.
Of course I am also thinking about open baffle loudspeakers, since I am very interested in them, or at least speakers with dipole radiation. But I see a large OB speaker and something of a hybrid. At low frequencies the baffle is too small and front and back sides "see" each other. But as frequency increases, the baffle transitions through and above the baffle step. Even if there is backside radiation, the large baffle is "in the way" of it getting to the listener. Many of these systems use a fullranger, or transition to a dome or horn tweeter that is only front firing. This is obviously not providing any rear-side acoustic output at HF whatsoever. Even when there is rear-side radiation, with a large baffle we are probably above what would be the baffle step for a closed box speaker. Even though the baffle is "open" this HF region seems to be more akin to closed box loudspeaker with a very wide baffle. This has be again thinking about the small vs large size loudspeaker in terms of soundstage, etc. and how this might influence the performance of a large OB type speaker.
A wavelet covers time and amplitude. A typical wavelet analysis as we've been seeing more of recently does this over a band.
Perhaps that's why Charlie dismissed them 🙂 It seems to me the principle explains all (?) aspects of wave propagation in a relatively simple way?
A wavelet is not a real (physical world) thing. It's a class of mathematical functions with compact support. There's nothing more to it. Just because you can write something in terms of its wavelet representation does not mean that it is actually comprised of wavelets physically. That's some pretty bad logic.
I think there remains some confusion between wavelets as employed by Huygens and wavelets as employed as mathematical tools.
Attached is one of the better diagrams I've found illustrating diffraction at the edge of an obstacle. The new wave fronts on the far side of the obstacle are simply the envelopes of the wavelets, and are constructed by drawing a line which is tangent to the leading edges of the wavelets.
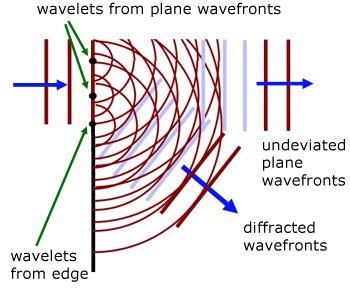
These tangential lines are shown in blue in the diagram and show how both the undeviated plane wavefronts and the diffracted wavefronts develop on the far side of the obstacle.
Attached is one of the better diagrams I've found illustrating diffraction at the edge of an obstacle. The new wave fronts on the far side of the obstacle are simply the envelopes of the wavelets, and are constructed by drawing a line which is tangent to the leading edges of the wavelets.
These tangential lines are shown in blue in the diagram and show how both the undeviated plane wavefronts and the diffracted wavefronts develop on the far side of the obstacle.
Attachments
If you excite a very short stimuli like e.g. a sinc (half a complete sinus e.g. only the positive part) you are in a wavelet world that is real - no? Here you can do envelope analysis instead of a steady state, windowed (i.e. a mean), analysis like FFT etc...
//
//
@Galu: It says it right on the picture "wavelets from plane wavefronts/edge". Look this is much like how I invoked the name "phantom source" in my own posts. There is no actual "source" at the edge where diffraction occurs, just as there are no real world "wavelets". These are just made up constructs to better explain/model the physics of diffraction, etc. This is, of course, very useful to explain/predict but I would not read into it more than that.
Getting back to one of my questions:
Why does the SPL increase by +6dB after N period of the wavefront are supported by a planar surface? What is N, and why?
Thinking about it in another way, the wavefront will eventually (in a loudspeaker) reach the baffle edge and will then expand into the greater space. This is supposed to mean that SPL will fall by 6dB, but that does not happen as long as the baffle is "wide enough". Why is that?
Maybe I need to post these questions in a more science-oriented forum?
Getting back to one of my questions:
Why does the SPL increase by +6dB after N period of the wavefront are supported by a planar surface? What is N, and why?
Thinking about it in another way, the wavefront will eventually (in a loudspeaker) reach the baffle edge and will then expand into the greater space. This is supposed to mean that SPL will fall by 6dB, but that does not happen as long as the baffle is "wide enough". Why is that?
Maybe I need to post these questions in a more science-oriented forum?
It seems to me there will be reflection from the baffle. Please ask in another forum and report back here, I would be interested to know what's happening too.
Hi Charlie,
My 2 cent thoughts, on infinite baffle, and baffle step when less than infinite.......
In line with your thread opening post, I view a baffle as simply a full-space divider.
So for me, the question becomes how big a space divider do i need for a given wavelength to behave like it's in half space. (and gain a full +6dB)
I know baffle step really means baffle ramp, and longer wavelengths will ramp down from +6dB to 0dB as wavelengths increase.
Whether it's a baffle, a driver diameter, a horn mouth, whatever...it seems to me to distill down to size vs wavelength.
Big waves make it around corners unscathed , little ones don't.
Why, I have no clue....and i sense that is part of the science you are asking about..
I call that kind of science real understanding...the kind that's underneath all the textbooks and models, and generally has to be dug up.. lol
My 2 cent thoughts, on infinite baffle, and baffle step when less than infinite.......
In line with your thread opening post, I view a baffle as simply a full-space divider.
So for me, the question becomes how big a space divider do i need for a given wavelength to behave like it's in half space. (and gain a full +6dB)
I know baffle step really means baffle ramp, and longer wavelengths will ramp down from +6dB to 0dB as wavelengths increase.
Whether it's a baffle, a driver diameter, a horn mouth, whatever...it seems to me to distill down to size vs wavelength.
Big waves make it around corners unscathed , little ones don't.
Why, I have no clue....and i sense that is part of the science you are asking about..
I call that kind of science real understanding...the kind that's underneath all the textbooks and models, and generally has to be dug up.. lol
Agreed!
As I said earlier, Huygen's secondary waves (wavelets) have no physical existence.
The Huygens-Fresnel principle is simply a clever tool for analysing wave motion, but it is not 'reality'.
Prof. Russel tries to explain basics...
Dan Russell's Acoustics and Vibration Animations
About "baffle step/loss"
Understanding Baffle Step and Diffraction
Finally… the point
When you change the wall to something the size of a typical baffle, you end up with something in between. At higher frequencies that see the baffle as sufficiently acoustically large, you end up with a 6 dB increase in output. At lower frequencies as you go through the transition region, you see a gradual reduction of output until the baffle becomes acoustically transparent and you are at a full 6 dB of reduction. And in that transition region at the edge of the baffle, you get that scattering effect described earlier which causes a series of peaks and dips. The severity of that is dictated by the size of the driver and the shape of the edge.
So, practical cases of loudspakers are always a combination of several types of sound radiation/diffraction phenomena. Wavelength of sound is most important factor, driver diameter, baffle dimensions and edge contour will modify the outcome. This is the in my mind the most important reason for multiway construction,with diffrent size of radiators and baffle for each, to remain in linear comfort zone for each unit. Ultimate low and high end will be compromized still...
ps. I'm not an engineer, so this kind of easy concept is quite enough for me! It took some years to get it anyway!
Dan Russell's Acoustics and Vibration Animations
About "baffle step/loss"
Understanding Baffle Step and Diffraction
Finally… the point
When you change the wall to something the size of a typical baffle, you end up with something in between. At higher frequencies that see the baffle as sufficiently acoustically large, you end up with a 6 dB increase in output. At lower frequencies as you go through the transition region, you see a gradual reduction of output until the baffle becomes acoustically transparent and you are at a full 6 dB of reduction. And in that transition region at the edge of the baffle, you get that scattering effect described earlier which causes a series of peaks and dips. The severity of that is dictated by the size of the driver and the shape of the edge.
So, practical cases of loudspakers are always a combination of several types of sound radiation/diffraction phenomena. Wavelength of sound is most important factor, driver diameter, baffle dimensions and edge contour will modify the outcome. This is the in my mind the most important reason for multiway construction,with diffrent size of radiators and baffle for each, to remain in linear comfort zone for each unit. Ultimate low and high end will be compromized still...
ps. I'm not an engineer, so this kind of easy concept is quite enough for me! It took some years to get it anyway!
Last edited:
Isn't it just mathematical modelling and terminology? Air is mixture of gases, mostly nitrogen, atoms and molecules get excited by driver membrane and vibrating compression/rarefaction pulses spread around. Scientists started to give names like soundwave, phase, frequency, wavelet etc. and units for them, and create formulas to calculate and predict consequences.
Gas molecules don't know about names or formulas!
Gas molecules don't know about names or formulas!
Last edited:
I don't know. I can imagine air molecules responding in a similar way to the wavelet theory. One would think it could be observed, say in a smoke chamber?