Something to lighten the mood

[Galu]

All this talk of whisky is driving me to drink!

 

[AllenB]

So the cop says to me please step out of the car. I said it would be easier if you got in.

 

[stv]

how to store the whisky?
if you had a square storage wall with dimensions of multiple barrel diameters, would the honeycomb pattern allow more barrels than the rectangular array at a certain dimension? and what would the dimension be?

 

[system7]

Ah, the packing problem! Works best in 8 and 24 dimensions. 😎

Curiosity got the better of me last night. I purchased a packet of Scott's Porage Oats.

The Packet is very helpful about the incomprehensible Scottish language.

It's awfy dreich oot the day.
Best keep the baffies on,
grab a bowl of Scott's and
keek out the windae, feeling Gallus.

Translation:
"The weather's terrible out there today.
So you should keep your slippers on,
enjoy a bowl of Scott's and just look out of the wondow,
you'll feel brilliant."

We used to have subtitles on English TV when Scots people were talking. 😀

 

[Galu]

What's a "wondow"?

 

[system7]

A priest, a minister and a rabbit walk into a bar…
The rabbit says: “I think I might be a typo”

 

[Galu]

how to store the whisky?
if you had a square storage wall with dimensions of multiple barrel diameters, would the honeycomb pattern allow more barrels than the rectangular array at a certain dimension? and what would the dimension be?

I believe the dimension to be a certain "square number", but I don't have a simple proof.

 

[mchambin]

how to store the whisky?
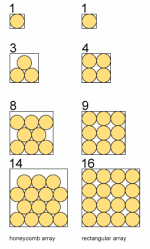
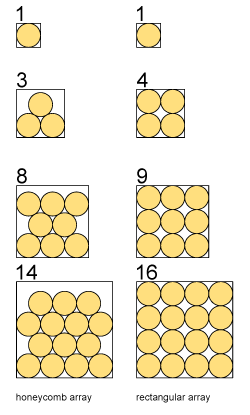
if you had a square storage wall with dimensions of multiple barrel diameters, would the honeycomb pattern allow more barrels than the rectangular array at a certain dimension? and what would the dimension be?

Pretty nice puzzle.
The honey comb storage becomes more efficient with increasing square room size.
I think I found the lowest size for this to happen.
I found a 3 digit number of barrel, their sum is 9.

 

[system7]

how to store the whisky?

if you had a square storage wall with dimensions of multiple barrel diameters, would the honeycomb pattern allow more barrels than the rectangular array at a certain dimension? and what would the dimension be?

I've been cheating. There is a calculator for this. You can look at this link without spoiling the problem if you want.

pack circles of radius 0.5 in a square of side 6 - Wolfram|Alpha

I got a number of barrels whose sum is 14...

 

[mchambin]

how to store the whisky?
if you had a square storage wall with dimensions of multiple barrel diameters, would the honeycomb pattern allow more barrels than the rectangular array at a certain dimension? and what would the dimension be?

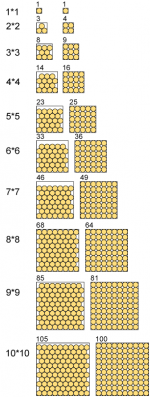
I found a 14 x 14 square where you can store 216 barrels honey comb way, better than 196 in the rectangular way.
BUT....

This is not the lowest size. There is a lower one.

It all boils to look for multiples of sqrt(3) that are a little bit under an even integer.

 

[stv]

There is a calculator for this. You can look at this link without spoiling the problem if you want.

now that is interesting!
it breaks out of the square or honeycomb pattern!

I did the (lazy) graphic approach...

 

[system7]

I got a bit side-tracked by the 7x7 one below. Wondered if you can get from the irregular solution arrangement of 49 to the cubic 49. I don't think you can. There isn't room to move things around beyond a certain point.

And you can't do anything with a cubic arrangement. It's rigid.

 

[Galu]

The square packing ceases to be optimal for squares after 49, 49 being 7 squared.

 

[system7]

Quite right.

The obvious square packing is optimal for 1, 4, 9, 16, 25, and 36 circles (the smallest six square numbers), but ceases to be optimal for larger squares from 49 onwards

Circle packing in a square - Wikipedia

At risk of turning this into an expanding Universe thread I am interested in the 3D problem.

Why is Iron 56 the most stable nucleus?

Iron-56 - Wikipedia

Must be packed very optimally. More research needed. 😀

 

[boswald]

With the honeycomb, you will need an outside wall of immense strength, as the barrels will behave like a liquid, and want to flow.
With aligned rows and dividers it takes very little to hold the barrels in place, the weight of each not trying to roll the one below.


About your rabbit joke, Steve- Linda and I were in our local supermarket, in the freezer aisle,
and I saw a packet labelled "cut up rabbi"..........I said "let's get out of here, they got Bob(Alper,a local rabbi who is a comedian, and actually opened for the Pope)"!!

 

[Galu]

Quite right.

However, the mathematical proofs of these packing problems look extremely complicated to me! 😱

 

[Galu]

Here's good crack at it!

https://www.quantamagazine.org/the-math-of-social-distancing-is-a-lesson-in-geometry-20200713/

 

[Galu]

P.S. I see mchambin's square root of 3 in the hexagonal packing part.

He knows what he is talking about!

 

[mchambin]

now that is interesting!
it breaks out of the square or honeycomb pattern!

I did the (lazy) graphic approach...

Lazy, not really, I would say: Foolproof.

I was expecting quite a large size, so neglected small sizes...and went over the right answer. :-(

 

[system7]

I spend a lot of time at Quanta Magazine. Good site.

Notice I was right about E8 and the Leech Lattice E24! Very interesting dimensions.

I was just playing with my balls:

Only got 7 useful ones really. He-4, C-12 and O-16 are particularly stable nuclei:

Nuclear binding energy - Wikipedia

I totally get Helium 4. Tetrahedron. Carbon 12 must be an empty hexagon and a triangle above and below. 3-6-3. Oxygen 16, I need more balls!

BTW, did we ever answer stv's question. It's 8x8 for unit balls or circles isn't it?