Yes. We're already on-board with that. https://www.diyaudio.com/community/...earization-by-fir.393435/page-38#post-7489069
Yep. Pretty much everything this thread is this thread is text book stuff today. The algorithms may evolve but the theory is historic. Anyway, the issue is not so much removing GD from the filters. The emphasis should be on removing GD from the speaker, IMO. But I understand there are always new individuals coming on board who haven't seen this stuff before. So threads like this are educational, and that's good. I just don;t have the patience for it any more. 🙂
Hi ICG, I do live too, and agree with your take on 15-20ms latency. I figure that to be total acceptable latency, so I substact mixer and processor fixed latencies form that, to get the amount of time a FIR filter has to work within. I use 12ms FIR filter latency as the goal to stay under.
I'm not sure what you mean by steep low-cut at 35-40Hz? Do you mean the subs high-pass filter? If so, that needs to be IIR, ime.
(I've never seen a horn sub large enough to go low enough, to be able to use a low-pass at 40 Hz.)
People may not have much control over their DSPs, as these frequently come built into their amplifiers / processors. And whenever they do, there are several preferences related to hardware, cabling, interfaces, heating, power consumption, jitter / noise, ADCs / DACs etc. that govern people's choices much more than tap count. And lastly, not everyone wants a software platform with an OS just for making a crossover and playing some music. For example, the ADAU1701 is a popular device used in many products.
Yes Sir, I'm aware that these techniques are old and tested. However, I just wanted to show how the linearised phase IIR LPF could be treated like a linear phase filter and used to make a linear phase crossover without FIR filters at all.
Similar techniques could be be used for 'removing' GD from speakers (pun intended). The maximum GD needs to be carried through across the entire band and thereby maintain linear phase.
Last edited:
Actually it is supposed to look more like the following. The low frequency issues we see are probably due to the non-optimised phase compensation.
Also, the individual passes are linear phase in their own right without FIR filters.
The optimization criteria in my MDS papers were linear-phase LPF (within its passband), minimum-duration impulse response, and steepest possible HPF transition-band slope. If the minimum-duration impulse constraint is removed, then a whole new world of possibilities opens-up, as shown by this and many other examples in this thread. Each of those solutions is as valid as mine. The definition of "optimal" depends entirely upon what one wants to optimize.
Maybe you could explain a little more what would be the advantage of your LR4 + phase linearisation lowpass over a simple 4th order lowpass used for a subtractive delay crossover.
Is its vertical lobing behaviour better ?
Regards
Charles
If you have a copy of my MDS paper, see section 2.2.3.2. When a simple 4th-order IIR LR filter is used as the basis for an MDS crossover, the lowpass response and highpass response are never in-phase with each other.
I guess I would still prefer the method that is using bessel lowpasses for cascaded subtractive delay crossovers so I can get a fourth order highpass.
Regards
Charles
Regards
Charles
Section 3.1.2 of the MDS paper. It's my preferred response, as well. However, I strongly recommend implementing it as FIR, section 3.1.1, if you have sufficient computational resources. The IIR version may be more complicated than it's worth.
The above is no better. It uses slight time misalignment (~600us at 100Hz) to get the said slope. If you see, the highpass is also 3rd order. This was why I first wanted to show the version where the highpass was FIR.
Ah, I hadn't noticed that until you pointed it out. There are many parameters that can be adjusted in this configuration. As with most design processes, adjusting one parameter affects the other parameters, sometimes in unexpected ways.
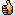
I've refined the phase compensation of the LR4 and the result is exactly how you predict !!! Only 3 APF biquads were used on top of the LPF, and the derived HPF is linear phase with a 4th order slope upto 20Hz below which there's no audio anyway. The net delay is about 12ms (constant).
Those with more biquad capabilities may add more APF biquads to further linearise the phase but it woudn't matter much due to the fast rolloff of the fourth order lowpass.
Unwrapped phase below. The red trace (HPF) is not visible as it under the black one (summed output) as it is essentially linear phase across the entire band. The blue trace (LPF) eventually departs but remains coherent upto almost 1.8 times the crossover by which frequency the magnitude has already dropped off by more than 20dB.
Last edited:
Incidentally, I happened to realise that a (much) better IIR-only linear phase Linkwitz Riley crossover could be obtained simply by using a different delay value in the above post, with absolutely no changes to the APF biquad parameters !!
While the new delay is 12.7ms, the symmetry of the derived HPF is retained beyond -100dB, as opposed to only -70dB in the above post. The HPF, as before remains linear phase throughout its passband and approximately linear phase elsewhere. The LPF phase becomes less important above 1.5x the cutoff, as its magnitude response would already have dropped off considerably by then.
For use at other crossover frequencies, simply scale the delay time and the center frequencies of all the filters/biquads alike.
While the new delay is 12.7ms, the symmetry of the derived HPF is retained beyond -100dB, as opposed to only -70dB in the above post. The HPF, as before remains linear phase throughout its passband and approximately linear phase elsewhere. The LPF phase becomes less important above 1.5x the cutoff, as its magnitude response would already have dropped off considerably by then.
For use at other crossover frequencies, simply scale the delay time and the center frequencies of all the filters/biquads alike.
Last edited:
I have a bit hard time to follow - let me ask a question - how would one implement such a crossover practically and what hardware would be needed? Also, what would be the implications of using real drivers (linearizing response, etc.)?
The processing hardware required for practical implementation of an MDS crossover requires some very basic capabilities:
The crossover filters discussed here are a diversion and the main topic is being discussed in the following thread:
https://www.diyaudio.com/community/...bal-phase-linearization-by-fir.393435/page-44
- Audio interface (I2S, SPDIF, analogue etc).
- IIR / FIR filtering capabilitiies as applicable. IIR only / limited tap FIR is also OK.
- Time alignment delay with good resolution (say 1 sample).
- Adjustable channel selection / mapping.
- Output summing / subtraction capabilities between channels for deriving other filters. This summing / subtraction needs to be after the delay stages.
The crossover filters discussed here are a diversion and the main topic is being discussed in the following thread:
https://www.diyaudio.com/community/...bal-phase-linearization-by-fir.393435/page-44
Forget drivers, the output reconstruction filters of DACs are more than capable of rendering any linear phase filter non-linear phase !!
Last edited:
In my program that creates MDS crossovers, I have it try three (potentially) different values of delay:
1. Delay at DC
2. Delay that produces maximum HPF transition band slope
3. Delay that produces best phase match at crossover frequency
The values are usually within ±1 sample, but not always.
Maybe I used a wrong delay in the first instance.. the new one is 608 samples at 48kHz... let me check again anyway.
Last edited:
The results above are not wrong, but the granularity of delay time used was much higher than the usual 1 sample resolution. The exact delay that was used for the -120dB symmetry case was 608.18 samples at 48kHz for which the closest value of 608 samples could be used in practice. The symmetry would still be great upto -60dB, as shown below.