The compression measurement was taken with a 80 Hz HPF. Depending on where the tuning sits, the SPL at the port tuning frequency might already be significantly reduced.
We'd also need to know the type of excitation signal. Was what was measured an RMS value (determined via sine sweep, stepped sine, or similar), or are the curves basically peak values created with stochastic noise or a multisine signal, which both have around 12 dB crest factor and would demand much less of the speaker.
That's good to hear, and I agree with the idea of checking the influence of slight vertical variations. I'd definitely also measure and compare different rotational axis - especially the very front of the speaker, also the center of the speaker.
To emphasize my previous point, I don't believe there's a fundamental reason why a turntable run should produce a completely different directivity chart than an NFS scan, especially if just in the high frequency region. But of course, both need to be set to measure the same thing. If the rotational axis and/or the measurement distance, or anything else of significance within the measurement setup or settings are different, there will be different results.
Because I don't think I've ever seen such an empirical comparison posted before, here's ours, with results, to provide something tangible, not just empty claims, to show both should generally yield close to the same result:
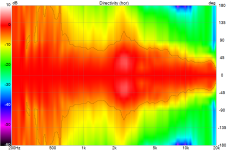
NFS:
Turntable:
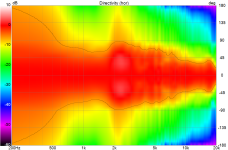
The NFS software, when asked for a CEA2034 output, reduces its point cloud of measuring points to two circular rings, that form the model of CEA2034; an abstraction and interpolation of a spherical space from two circles. Erin @bikinpunk will know if the NFS tweaks that CEA2034 output to weight in what the robot knows due to what it measured and make the CEA2034 more precise according to data.
In the case of th eight-fold solana waveguide it is very easy to come to differing results: four of the protruding geometries are interrupted by ports, which will definitely interfere with very short wavelengths. And the eight valleys can easily become beaming devices, insofar as they allow very wide lower frequencies and the throat would need to be optimized to make the top end very wide as well.
I think its a complex geometry, and if you want to stick to the eight-fold approach, optimization and simulation along the single channels is required: along the valley, the bulges, and the bulges with entry ports.
I am not surprised you could not catch this at first, although it should be observable with observation scripts that aim at the specific angles. But I would still like to understand the technical reasons for differences between the NFS and the turntable measurements.
In the case of th eight-fold solana waveguide it is very easy to come to differing results: four of the protruding geometries are interrupted by ports, which will definitely interfere with very short wavelengths. And the eight valleys can easily become beaming devices, insofar as they allow very wide lower frequencies and the throat would need to be optimized to make the top end very wide as well.
I think its a complex geometry, and if you want to stick to the eight-fold approach, optimization and simulation along the single channels is required: along the valley, the bulges, and the bulges with entry ports.
I am not surprised you could not catch this at first, although it should be observable with observation scripts that aim at the specific angles. But I would still like to understand the technical reasons for differences between the NFS and the turntable measurements.