OK, this is easy. The kinetic energies of the balls equal the amount of work you had to do (i.e. the energy you had to spend) to bring them up to the top of the tower (at least if they didn't fell off the sky suddenly).
If you could come up with the same analogy for the loudspeaker device, it would be great!
Off topic / language corner: When I write "to bring them up to the top of the tower" is it understandable for you, native speakers, that it means "to take/carry them there" or not? 😱
That's what I meant.
I only know this equation (Thiele/Small parameters - Wikipedia):
An externally hosted image should be here but it was not working when we last tested it.
Does it hold or not? What else would it mean, if not that the efficiency will stay the same?
The 0 indicates that is a reference value of some kind. The acoustic efficiency varies with frequency, I gave an unnormalised expression in an earlier post, and so your two cases will vary differently with frequency over the passband of the driver because other components of the various impedances have not been scaled to align them (there was a plot by someone earlier showing this). Your two cases may tend towards the same value at high frequencies above the driver passband.
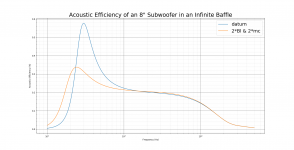
The edit button seems to have gone. This is the acoustic efficiency of an 8" subwoofer in an infinite baffle using a conventional lumped model for the driver with and without doubling Bl and mc. Not too dissimilar to the earlier plot. Note this was a few minute hack without any checking and so may not be immune from errors.
Attachments
You're doing fine. 😉 Just can't figure out what your 'stumbling block'/'blind spot' is? [if that translates well enough].
GM
This is strictly peak mid band efficiency [up around 1 kHz for woofers].
GM
Right, notice how the lines converge at ~1 kHz as the math predicts.
GM
Good luck with it, really sucks when one 'can't see the forest for the trees'. 🙁 Anyway, looking forward to what the 'missing link' is. 😉
GM
GM
I'm learning the basics again -
In the gravitational field the situation is much simpler because the force is proportional to mass and you can't get rid of mass, i.e. there's allways some potential energy. But current through a coil in a magnetic field can be switched on and off. So when I switch on the current through the coil, its potential energy will be the energy needed to build up the magnetic field of the coil?
In the gravitational field the situation is much simpler because the force is proportional to mass and you can't get rid of mass, i.e. there's allways some potential energy. But current through a coil in a magnetic field can be switched on and off. So when I switch on the current through the coil, its potential energy will be the energy needed to build up the magnetic field of the coil?
Isobaric-theory may be useful?
If you change from a singel woofer system to an isobaric system (two woofers), in practice you double the magnetic field and you double the moving mass, while keeping the Sd unchanged.
Example (identical woofers in both systems): A 20 liter cabinet gives the singel woofer an F3 = 50Hz. A 10 liter cabinet gives the isobaric system an F3 = 50Hz. A 20 liter cabinet gives the isobaric system half an octave deeper bass F3 = 35Hz. But with the two isobaric systems you have to double the amplifier power to produce the same SPL as with the singel driver. This might illustrate that it is difficult to double the mass and double the magnet field, and keep all the other variables unchanged.
If you change from a singel woofer system to an isobaric system (two woofers), in practice you double the magnetic field and you double the moving mass, while keeping the Sd unchanged.
Example (identical woofers in both systems): A 20 liter cabinet gives the singel woofer an F3 = 50Hz. A 10 liter cabinet gives the isobaric system an F3 = 50Hz. A 20 liter cabinet gives the isobaric system half an octave deeper bass F3 = 35Hz. But with the two isobaric systems you have to double the amplifier power to produce the same SPL as with the singel driver. This might illustrate that it is difficult to double the mass and double the magnet field, and keep all the other variables unchanged.
The work done against a gravitational field is not particularly illuminating when considering the energy transfers in a driver. The magnetic field is not involved in (directly) storing energy but transferring it from one form to another. In this case between mechanical and electrical energy.
When energy is flowing rather than a discrete event like lifting a weight against the force of gravity the energy transfer is normally written in terms of rate of energy transfer (power) rather than energy.
The rate of work done (power) by a force is the product of force and the rate of displacement (velocity) in the direction of the force. Mechanical impedance, Z, is force divided by velocity and is a quantity engineers tend to use to examine energy transfers. Electrical impedance is voltage divided by current and electrical power is again the product of voltage (what's doing the forcing) and current (what flows).
Mechanical energy is present in a reversible form as kinetic energy of the motion and potential energy in compressing the suspension and irreversible form as heat. Likewise for electrical energy with the inductance and capacitance being reversible and the resistance irreversible. And again for acoustical energy.
Can we stop thinking for a moment about suspension and its compression? Let's suppose the coil can just move freely along its axis in a magnetic field, and let's say it's all we have. When connected to an AC voltage it will oscillate back and forth, right? It will have kinetic energy for any non-zero velocity, with a peak value when the velocity is at maximum. Then there must be some form of this energy somewhere when the coil is in the position(s) with zero velocity. What is it, where did it come from and where does it go in the end?
I guess I must have been missing in school that day, but it's really this very basic question that I can't help myself with...
- Oh, and I've just noticed this thread was rated as "terrible" so I suppose I'd better stop altogether 😀
Last edited:
It is required to work out the acoustic efficiency of a driver.
It looks like you may not fully understand the difference between a forced response and a free response of a system.
To repeat. The coil in a magnetic field does not store energy in the manner of compressing the suspension. It transfers energy between electrical and mechanical forms. So if you look at the mechanical side only and discard the forces due to the stiffness of the suspension, the damping of the suspension, the resistance and reactance of the air,... it will leave the force arising from current flowing in the coil to balance the force arising from the inertia of the coil/cone assembly. By considering only the mechanical side as the system the force arising from the coil is external (i.e. the energy associated with it is electrical not mechanical and is external to the system being considered). To model the complete driver you need to expand the system to include the electrical and acoustical side to leave just the work supplied at the terminals and the work done on the air as external.
The above is a Newtonian view (Newtons laws) involving force, mass, stiffness, damping, displacement, velocity, acceleration,... and is the starting point (and ending point for most people) when it comes to equations of motion. There is an alternative Hamiltonian view of the equations of motion involving things like potential and kinetic energy but it is not the place to start.
Gravity example:
- the force acting the the balls is F = M x g
- the change of kinetic energy of the falling ball is W = F x D, where D is the distance of the fall (ignoring any friction or other mechanical losses)
Loudspeaker / magnetic field:
- the force acting on the cone is F = BL x I
- the change of kinetic energy of the cone is W = F x D, where D is the distance the cone has moved (ignoring any mechanical losses)
Do you see how the example with the falling balls is analogous to your loudspeaker cone question?
It is not really efficiency per se that makes the difference. The low efficiency of louspeakers is not from the electrical to mechanical conversion, but rather from the mechanical to acoustical conversion. As a general statement, electromagnetic motors are really efficient (however, not what is optimized in a loudspeaker, clearly).
To answer your question, two situations can be discerned: the steady (periodic) state and the impulse. Both are to be analyzed in terms of the flow of energy. What you forgot to account for in your thought experiment is that to drive current through the coil requires voltage. It is the instantaneous product of voltage and current which equals electrical power. Integrating over time, one has the electrical work done by the power supply on the driver. Now for the two situations.
A driver at rest being driven by a step function, and thus accelerated, will produce correspondingly large back electro-motive force (emf). In order to maintain the current, one will have to proportionately increase the input voltage and thus the input power.
This must not be confused with the typical steady state analysis where a periodic signal of a given frequency is applied to the coil. In this case, far from the resonance of the driver, neglecting acoustical radiation and the various mechanical losses, the electrical power integrated over a complete cycle must vanish. This is the definition of steady state. There will be no net energy transfer as energy will be moved in and out of the driver depending on the relative phase of the instantaneous current and voltage. Concretely this energy ends up being dissipated (or stored) by the electrical components in the circuits (wires, resistances, inductances, capacitors, etc.). The same happens theoretically at resonance. However, in this case the energy stored in the mechanical oscillating circuit diverges to infinity. Physically speaking this means that one can no longer neglect the various dissipative phenomenons (losses, one of which is sound!). Thus, steady state will be reached when the energy flowing in the the mechanical oscillator (the driver) will equal the energy leaking out through the dissipation in the non-ideal suspensions, the air viscosity, the sound radiated, the core losses, etc. This is essentially what gives real oscillatory systems a finite Q such that their response does not blow up at resonance.
I hope this what somewhat clear.
Regards,
Geoffroy
To answer your question, two situations can be discerned: the steady (periodic) state and the impulse. Both are to be analyzed in terms of the flow of energy. What you forgot to account for in your thought experiment is that to drive current through the coil requires voltage. It is the instantaneous product of voltage and current which equals electrical power. Integrating over time, one has the electrical work done by the power supply on the driver. Now for the two situations.
A driver at rest being driven by a step function, and thus accelerated, will produce correspondingly large back electro-motive force (emf). In order to maintain the current, one will have to proportionately increase the input voltage and thus the input power.
This must not be confused with the typical steady state analysis where a periodic signal of a given frequency is applied to the coil. In this case, far from the resonance of the driver, neglecting acoustical radiation and the various mechanical losses, the electrical power integrated over a complete cycle must vanish. This is the definition of steady state. There will be no net energy transfer as energy will be moved in and out of the driver depending on the relative phase of the instantaneous current and voltage. Concretely this energy ends up being dissipated (or stored) by the electrical components in the circuits (wires, resistances, inductances, capacitors, etc.). The same happens theoretically at resonance. However, in this case the energy stored in the mechanical oscillating circuit diverges to infinity. Physically speaking this means that one can no longer neglect the various dissipative phenomenons (losses, one of which is sound!). Thus, steady state will be reached when the energy flowing in the the mechanical oscillator (the driver) will equal the energy leaking out through the dissipation in the non-ideal suspensions, the air viscosity, the sound radiated, the core losses, etc. This is essentially what gives real oscillatory systems a finite Q such that their response does not blow up at resonance.
I hope this what somewhat clear.
Regards,
Geoffroy
For this analogy to work, you have to think of gravitational field as electric field, gravitational potential as voltage, mass as charge and velocity as current. The electrical force is proportional to charge times electric field (that's coulomb's law) which is the gradient (variation over a distance) of the electric potential a difference in which is measured in volts. You can't get rid of charge (forget negative charge for a moment), there's always some electrical potential energy (when referenced to some other charged object, same as gravity). But masses in movement can be started or stopped, irrespective of the gravito-magnetic effects. See what I just did, complete analogy! However, be wary of analogies in physics, they are often false. In this case, the last statement is sketchy. In as much as magnetism can be seen as a relativistic correction to the theory of electric forces, this gravito-magnetic effect requires relativity. However, at this point, the two theories are more and more unlike each other. And trust me, gravity is WAY more complicated than electromagnetism. (Or even QED at that!)
In some sense, the potential energy IS the magnetic field building up. It starts at zero and ends up at a maximal value when the current is stable.
Regards,
Geoffroy
Thank you very much Geoffroy for your effort. I'll go through it several more times but I'd say I'm slowly getting the feeling for it.
In fact, I didn't forget about that but from a quick look at the resulting electrical impeadnces of the two cases (far enough from resonance), I concluded that they are "about the same" and thought that it couldn't make that difference - which I'm now beginning to acknowledge was completely wrong idea. The efficiency of electrical-to-mechanical energy conversion is really that low for a loudspeaker driver. The vast majority of the input power is really dissipated as heat on the voice coil.
The conversion between electrical and mechanical energy is assumed to be 100% efficient in most models (i.e. the work added/subtracted from the electrical side is exactly equal to the work subtracted/added to the mechanical side). The electrical-to-acoustical conversion shown in the plot earlier is low but the main culprit here is the large impedance mismatch between the light air and the heavy coil/cone assembly. Stick the driver in water and the electrical-to-acoustical efficiency jumps up a lot.
Comparing the work taken from the amplifier at the driver terminals with the work done on the air to create sound is the efficiency of the driver. You are correct that most of the work supplied is dissipated in the voice coil with some unwanted dissipation in the suspension and only a small amount of wanted dissipation in the air. All the other internal forms of energy related to mass, stiffness, inductance, capacitance are reversible and within the system. The reactance of the air is external.
You are allways heating up the voice coil so how that could be 100% efficient even in the model? 😕
- Status
- Not open for further replies.