The PDF says on page 9, "Measurement must average on enough independant positions : so move microphone to cover a volume large enough : a 10m scanning distance is a good basis. Another way is to cover a volume with dimensions of about 1/5th of corresponding room dimension, it has beeen tested to give reliable results down to Tf."
Would this need to be adapted to our small listening rooms? How?
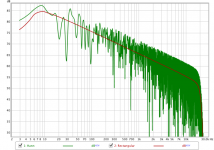
Your image shows a Hann window for the RTA, a rectangular window should be used with noise sources. Pink periodic noise works much better than pink random noise at the low end (need a lot of averaging time at LF for pink random noise as it is only pink after a sufficiently long averaging time elapses, whereas PN is synthesised to be precisely pink within each period).
Most of the louspeakers can benefit from eq even above 700Hz, I have rarely seen speakers that could not be, some just a bit, improved at mid/high frequencies. Flat response and smooth DI is quite rare...(I never measured Earl loudspeakers 😉
As Earl said, the Olive studies do not give the recipe for in-room measurements. Harman defines how the loudspeaker various responses should ideally be. But in a room, at lower frequencies, even with an ideal loudspeaker, you have to eq more or less.
Interesting about this is to read Olives's paper on room correction :
https://docs.google.com/file/d/0B97zTRsdcJTfY2U4ODhiZmUtNDEyNC00ZDcyLWEzZTAtMGJiODQ1ZTUxMGQ4/edit?hl=en&pli=1
John, why is a rectangular window better suited for pink noise?
Isn't periodic noise counterproductive with the spatial averaging method discussed here?
jlo, could or should the averaging method be used for setting the response from subwoofer to satellites?
The procedure I'm thinking about would be:
- measure sub with MMM technique
- EQ to desired cutoff frequency and slope
- measure each satellite with MMM technique
- EQ to desired cutoff frequency and slope
- measure combined response of sub and satellites with MMM technique
- tweak crossover region
The procedure I'm thinking about would be:
- measure sub with MMM technique
- EQ to desired cutoff frequency and slope
- measure each satellite with MMM technique
- EQ to desired cutoff frequency and slope
- measure combined response of sub and satellites with MMM technique
- tweak crossover region
Thank you for this! I actually do use Pink PN.
The other discussion about setting xos around 200Hz - they really are pain in the a.. for us diyers. It is fundamental to go outdoors at least once, then you get some reference and see how things change when you drag the gear back indoors again. Indoors we need many different measurements and let us not forget auditioning!
Thanks guys, sounds like it is worth a shot. Dumptruck yes it is custom analogue and not standard electrical 2nd order or 4th order. The desired result is accoustic 4th order bessel slopes.
Does PCD allow you to design to a target accoustic response in the active or only to a target electrical response? My active basically simulates a passive network so if I work out the passive transfer function I already have the active 🙂
edit: spekr that is pretty much what I am thinking of doing, in my case the subs are the stands for the satelites. (and in my case the "SUBS" will play up to around 200Hz)
Tony.
Does PCD allow you to design to a target accoustic response in the active or only to a target electrical response? My active basically simulates a passive network so if I work out the passive transfer function I already have the active 🙂
edit: spekr that is pretty much what I am thinking of doing, in my case the subs are the stands for the satelites. (and in my case the "SUBS" will play up to around 200Hz)
Tony.
Last edited:
Windowing is required for periodic signals whose period is not an exact integer fraction of the measurement span. For periodic noise (with an appropriately matched RTA length) the signal is always exactly periodic within the span, for random noise signals there is no period and windowing alters the spectral balance.
No, it would be pretty much the ideal excitation. A 16k PN sequence at 48 kHz provides covers the whole span to 24 kHz every 340 ms or so, contributing broad spectral coverage for the positions the mic is moved through. Worst would probably be a typical measurement sweep, unless the mic was moved at a glacial pace or the sweep was very short.
Yes, if you mean by visually lining up the response to the acoustic target overlay (which you can set in the individual driver graphs). In the active section you can enter your own coefficients for any shape HP/LP, and IIRC there are four or five PEQ boxes as well.
I do not think your plan to use averaged measurements to find the time offsets makes any sense though, does it? That trick hinges on simulating at the mic location relative to the baffle in 3D at the exact point where you measured the driver interference, and if you've been running around the room with the mic averaging while measuring the interference...
I didn't read all 15 pages here, but here's my opinion/method anyway, in case it helps someone.
First of all, pink noise is equal energy per octave, while white noise is equal energy per decade of frequency. Since we hear in octaves, and therefore like to plot curves in octaves, and since you might burn out a tweeter running white noise for long, we go with pink when we use noise for calibration (sustained pink noise can burn out tweeters too. Be careful).
Any typical living room will be full of reflective paths. They create comb filter effects at any listening position except right near the speaker diaphram. These comb filter cancellations can be quite severe (6 - 15dB from my experience). The good news is that because of the multiple paths, each of which create cancellations at individual frequencies, when all mix at your ear, most cancellations are largely filled in by energies from alternate reflection paths. The bad news is that this doesn't usually happen very well below about 300HZ, where many rooms won't effectively have very many different reflection paths due to the size of the wavelengths relative to the size of the room. That's where you get into what's been called the Shroeder frequency region. This is probably the main source of "boominess" in most cases. I generally only try to use high resolution EQ (parametric or graphic) below about 300 HZ because of this. Above 300HZ I depend on multi-section (4 in my case) Baxandall tone controls.
Because many rooms have parallel walls, there will also be resonance issues. A resonance has a start-up and decay time. Measurement techniques that use a pulse won't see the resonance because of the start-up time. Measurements that use a slow swept sinewave will see the resonance, but not how the system reacts to transients in actual music. Actual music is full of both transients and sustained notes, so how do you optimize for both?
Tone bursts in gaussian envelops are among the more sophisticated measurement techniques, but leave you with the question of how long the burst should be. If you optimize the system for transient information only, then sustained notes in the music will be off, and vice versa. So then what? Compromise.
What I do is use pink noise, cal'd mic at listener position initially, 1/6th octave RTA with averaging turned on (an accumulation mode since pink is really only equal energy per octave over time of at least many seconds, and more time is more accuracy). I aim the mic very carefully at the tweeters (one speaker eat a time) knowing that anything else will give erroneous results due to the very small size of the wavelengths at high frequencies (unless the mic is specifically designed to be aimed differently). In fact, I largely ignore what the mic says for above 15kHZ just because of how easily this can be off enough to give wrong info. I remind myself that I'm not developing a new world best tweeter, I'm really just calibrating a tri-amp'd system and EQing it for the room to whatever degree is practical.
I use active parametric or high res graphic EQ for the area below about 300HZ, never trying to pull up a cancellation, only trying to reduce excessive peaking, and then I use my 4 section Baxandall tone controls for EQ of anything and everything wideband from there. Above about 300 HZ, it's my opinion that only gradual changes in EQ are desirable. Shelving usually creates abrupt EQ changes that can draw attention to a specific frequency. Baxandall is a variable slope thing so it's much less likely to draw attention like shelving can.
After all of this, I'll check with the cal'd mic in other parts of the room, but give those measurements less priority than the direct "sweet spot" listener position measurements, where I'll sit when I'm into serious listening.
It would be wise of me to also do burst measurements or a slow swept sinewave measurement to get a better look at any room resonance issues, but frankly I'm too lazy. I compensate for that by ear when I'm all done with the above, if I think I need to.
Then mix up a spanish coffee with no sugar, no nutmeg, no whatever else they put in those; just the booze, the coffee and maybe some whipped cream on top, and call it good.
Then for the next week I'll mess with the Baxandall tone controls until I get the sound that works best for my room, typical program material and my aging ears. If your speakers are very good, you might notice that there's a fairly significant variation in how various program material is EQ'd, so I may vary the tone controls from time to time to get the most enjoyment out of a particular song.
The ear-brain mechanism can do a significant amount of multi-band EQ itself, thereby adapting to much of the inaccuracy over time. You can spend huge amounts of time playing with all the latest calibration techniques, but having done most of that, I say perfection is not possible for a long list of reasons, and these techniques that I use seem plenty enough on the bottom line.
First of all, pink noise is equal energy per octave, while white noise is equal energy per decade of frequency. Since we hear in octaves, and therefore like to plot curves in octaves, and since you might burn out a tweeter running white noise for long, we go with pink when we use noise for calibration (sustained pink noise can burn out tweeters too. Be careful).
Any typical living room will be full of reflective paths. They create comb filter effects at any listening position except right near the speaker diaphram. These comb filter cancellations can be quite severe (6 - 15dB from my experience). The good news is that because of the multiple paths, each of which create cancellations at individual frequencies, when all mix at your ear, most cancellations are largely filled in by energies from alternate reflection paths. The bad news is that this doesn't usually happen very well below about 300HZ, where many rooms won't effectively have very many different reflection paths due to the size of the wavelengths relative to the size of the room. That's where you get into what's been called the Shroeder frequency region. This is probably the main source of "boominess" in most cases. I generally only try to use high resolution EQ (parametric or graphic) below about 300 HZ because of this. Above 300HZ I depend on multi-section (4 in my case) Baxandall tone controls.
Because many rooms have parallel walls, there will also be resonance issues. A resonance has a start-up and decay time. Measurement techniques that use a pulse won't see the resonance because of the start-up time. Measurements that use a slow swept sinewave will see the resonance, but not how the system reacts to transients in actual music. Actual music is full of both transients and sustained notes, so how do you optimize for both?
Tone bursts in gaussian envelops are among the more sophisticated measurement techniques, but leave you with the question of how long the burst should be. If you optimize the system for transient information only, then sustained notes in the music will be off, and vice versa. So then what? Compromise.
What I do is use pink noise, cal'd mic at listener position initially, 1/6th octave RTA with averaging turned on (an accumulation mode since pink is really only equal energy per octave over time of at least many seconds, and more time is more accuracy). I aim the mic very carefully at the tweeters (one speaker eat a time) knowing that anything else will give erroneous results due to the very small size of the wavelengths at high frequencies (unless the mic is specifically designed to be aimed differently). In fact, I largely ignore what the mic says for above 15kHZ just because of how easily this can be off enough to give wrong info. I remind myself that I'm not developing a new world best tweeter, I'm really just calibrating a tri-amp'd system and EQing it for the room to whatever degree is practical.
I use active parametric or high res graphic EQ for the area below about 300HZ, never trying to pull up a cancellation, only trying to reduce excessive peaking, and then I use my 4 section Baxandall tone controls for EQ of anything and everything wideband from there. Above about 300 HZ, it's my opinion that only gradual changes in EQ are desirable. Shelving usually creates abrupt EQ changes that can draw attention to a specific frequency. Baxandall is a variable slope thing so it's much less likely to draw attention like shelving can.
After all of this, I'll check with the cal'd mic in other parts of the room, but give those measurements less priority than the direct "sweet spot" listener position measurements, where I'll sit when I'm into serious listening.
It would be wise of me to also do burst measurements or a slow swept sinewave measurement to get a better look at any room resonance issues, but frankly I'm too lazy. I compensate for that by ear when I'm all done with the above, if I think I need to.
Then mix up a spanish coffee with no sugar, no nutmeg, no whatever else they put in those; just the booze, the coffee and maybe some whipped cream on top, and call it good.
Then for the next week I'll mess with the Baxandall tone controls until I get the sound that works best for my room, typical program material and my aging ears. If your speakers are very good, you might notice that there's a fairly significant variation in how various program material is EQ'd, so I may vary the tone controls from time to time to get the most enjoyment out of a particular song.
The ear-brain mechanism can do a significant amount of multi-band EQ itself, thereby adapting to much of the inaccuracy over time. You can spend huge amounts of time playing with all the latest calibration techniques, but having done most of that, I say perfection is not possible for a long list of reasons, and these techniques that I use seem plenty enough on the bottom line.
Last edited:
All data sampling is windowed, the question is why is a rectangular window better for random noise than say any other window. I don't see how it "alters the spectral balance". IMO a rectangular window is not the best for random signals. Matched periodic noise is the better choice, agreed, but that wasn't the question.
hmm good point on the time info. What I have been struggling with for the most part is getting measurements where I have smooth phase data in my crossover region.
I did the first proto of the filter with in room pink noise measurements (at a fixed point) (1 octave smoothed to get phase looking ok) and the result was reasonably good from an on axis SPL point of view, but phase matching (via a reverse null test) was not very good at all.
I opted for in room because my outside measurements weren't much better below 200Hz AND did not take into account room gain. My logic was that for my particular room, having the room gain in the measurements would allow me to deal with it in the filter transfer function rather than just a crude level adjustment accross the whole freq band.
I guess the only way to find out is to try the mmm. I suspect it will be better than my fixed point pink noise measurement 🙂
I'll have to have a closer look at the PCD active section, as I was not aware it was that flexible. It won't work for my circuit topology but is good to know I have that up my sleeve should my own circuit not work out.
Tony.
Last edited:
I don't think that is what you meant to say. A Decade is roughly 3 Octaves, i.e. also logarithmic.
It wasn't a quiz, it was a suggestion of something you could do if you felt any inclination to collect some data to use as a basis for your opinion.
Thanks for the correction. I had to refresh my memory on this. White noise has equal strength over a linear scale of frequencies while pink has equal energy over a log scale of frequencies. Pink has a 3dB/octave rolloff compared to white.
After thinking about my previous statement above, I'm thinking I really should do a slow swept sinewave as well, since it will bring to life any room or driver resonances, which I may want to attenuate.
Last edited:
My opinion is based on the theory, which I know pretty well.
Those results are not what you said would happen though. There is no "spectral shift" only a variance due to the random nature of the signal and a finite number of averages, probably one from the look of it. With enough averages the two will converge to the same result. And I suspect that the green curve is not just a rectangular window, but a periodic noise source as well. Because a non-periodic noise will still have uncertainty even with a rectangular window. The two windows should converge at about the same rate for a broadband signal.
It is a periodic noise signal, I specifically said "Try applying a non-uniform window to a loopback measurement of periodic noise". You seem to start from an assumption that everyone is an idiot and if something doesn't look right to you, it's wrong, which is probably why exchanges with you quickly become fractious. If you were to moderate those assumptions, or drop them altogether, you and the world would probably get along a lot better.
That result will not converge with averaging. Periodic noise is not some random collection of sample values, it is a specific, periodic sequence of values chosen to produce a specific spectrum (usually by starting with the spectrum and transforming it back to the time domain). Applying a window to that sample set produces a different sequence with a different spectral balance, which is what I said (spectral shift is your phrase). In the simplest case of taking an FFT of successive blocks of the input data whose length matches the FFT and sequence length the result is exactly the same for every block since the data is exactly the same for every block - that is the point of periodic noise. There are many possible different results depending on the point in the sequence at which capture started, but the result won't change until capture is stopped and started again from some other point. If the FFT is updated at a shorter interval (e.g. a 64k sequence might chunk the input into 8k blocks and update the FFT for each new block, giving 87.5% overlap with the previous block) there will be correspondingly more spectra, one for each unique sample set that results from applying the window at the different positions (8 positions for that example) but they will still not come anywhere close to averaging to the desired spectrum. I hope that is sufficiently clear, but I won't be commenting further in this topic regardless.