andy_c said:
I guess it depends on what else is done, frequency compensation wise. Suppose you shunt-compensate the LTP and/or the VAS with R-C's for frequency compensation instead of using Miller compensation.
Your VAS HF output impedance may then be limited to a couple of hundred ohms or perhaps even higher, a k-ohm or so (like the Otala amp, whose VAS collector has no feedback-compensation to lower its high frequency output impedance, and is just loaded with two parallel 2k2 resistors
).
John,
Was the output stage a Locanthi-style "T-circuit" or a two-stage with no predriver? If the latter, it makes sense. If the former, I'm stumped.
Edit: John, I see you tweaked your post a bit. My reply was to your original, which I thought referred to a power amp. Now I see it refers to an op-amp.
Was the output stage a Locanthi-style "T-circuit" or a two-stage with no predriver? If the latter, it makes sense. If the former, I'm stumped.
Edit: John, I see you tweaked your post a bit. My reply was to your original, which I thought referred to a power amp. Now I see it refers to an op-amp.
Mr.Curl.
I am not technically competent enough to engage in the current feedback debate but I am intrigued about the mention of the AD825. Many years ago Linsley Hood (and Gordon King I think) in the UK were both advocating low "settling time" as an objective indicator of an amp's inner health and subsequent subjective approval in listening tests. Is there any work done on the correlation between settling time and favourable listening experience? (The AD825 is fairly low) I raise this because as a layman I struggle with the theory of feedback but can look up parameters on a data sheet.
Any thoughts? Cheers, Jonathan
I am not technically competent enough to engage in the current feedback debate but I am intrigued about the mention of the AD825. Many years ago Linsley Hood (and Gordon King I think) in the UK were both advocating low "settling time" as an objective indicator of an amp's inner health and subsequent subjective approval in listening tests. Is there any work done on the correlation between settling time and favourable listening experience? (The AD825 is fairly low) I raise this because as a layman I struggle with the theory of feedback but can look up parameters on a data sheet.
Any thoughts? Cheers, Jonathan
Jonathan, I don't know. Andy, the output stage might have been quasi comp. with extra followers. I will have to check. I have a good idea why, but I would just be laughed at until someone 'discovered' the same sort of thing, themselves.
john curl said:
There have been a number of reports here (in MikeB's symasym thread for one) of this resistor reducing simulated and/or measured distortion. As far as I can tell, what's going on is that there's a significant nonlinear load presented to the VAS in the absence of the resistor. With the resistor present, even though the VAS is driving a load of lower impedance, the linearization of the impedance by the parallel resistor is more than making up for the reduced load impedance.
That's my guess anyway. I have no proof. I have not seen reports of this happening with power amps using Locanthi's "T-circuit" or other circuits having a very high and linear input impedance.
John and Glen,
I'm "posted out" here! 🙂 I'm listening to tunes at the moment and will return tomorrow after my sleep gives me a new virtual posting "dick splint" 😀
I am using shunt resistor Vas, I believe it depends on the current that runs in Vas. In my case, the bias of Vas is 4mA, shunt resistor 300uV not cause distortion. attenuation of 20dB in open loop in low frequencies (I not need a lot of feedback at low frequencies )😀
andy_c said:
Hi andy
You have any example to measure IMD in LTspice?
I would like to simulate in my circuits....
The more linear resistor loaded VAS , especially in the "first watt realm" can have very low THD. Without the loading , run of the mill.
depending on the VAS current a "window" appears where THD really drops. Too much loading or too little.. Thd soars.
This effect can be heard in low to moderate listening levels , at high levels where the EF is already acting as a load , not as apparent.
LT PIM simulation.. go for it, andy !!
OS
Attachments
andy_c said:
Hasn’t the term “fortuitous null” been used before? Single frequency / amplitude tests don’t really mean much as far as overall performance goes.
I don’t buy the “swamping the non-linear load” argument. By bunging a resistor onto the VAS you aren’t getting rid of the non-linear load at all (the driver or pre-driver stage is still connected), you are just bunging a linear load in parallel with it.
The non-linear part of the VAS load is still going to cause distortion, and you’ve just added more due to the drive requirement for that added resistor.
john curl said:
Lower VAS gain = lower Miller capacitance and therefore higher slew rate with all else being equal.
Pete B.
G.Kleinschmidt said:
Constant part of the resistance is lower, and it's relative variations are much lower, it causes lower percent of distortions as the result.
G.Kleinschmidt said:
It is analogous to the acoustic suspension loudspeaker where the lower and more linear compliance of the air load is in parallel with the less-linear but higher mechanical compliances.
Consider a 1K linear load in parallel with a 100K non-linear load. You going to claim that it will not be more linear - at least open loop?
Wavebourn said:
You have no idea what you are talking about.
PB2 said:
I don't see how the analogy is valid here. We are talking about adding an increased load that will (especially under "swamping" conditions) dramatically increase the current swing in both the VAS and the input stage.
That WILL result in greater non-linearity from the VAS and the input stage. The only way you are likely to get a lower measured result in a real-world, closed loop amplifier with a resistive VAS load is if there is a "fortutious null" with some other non-linearity, at a specific ampitude and frequency.
Regarding the 1k Vs 1k//100k load example, with the the latter in a closed loop system you cannot neglect:
A) The increased distortion caused by a 100 fold increase in required drive current.
B) The fact that the non-linear load is still present.
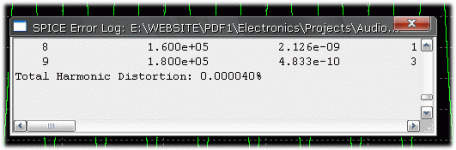
My simulations:
1KHz, negative feedback ~33dB (resistor-load Vas) 50Wrms
Harmonic Frequency Fourier Normalized Phase Normalized
Number [Hz] Component Component [degree] Phase [deg]
1 1.000e+03 2.393e+01 1.000e+00 -0.01° 0.00°
2 2.000e+03 3.390e-04 1.417e-05 -140.29° -140.28°
3 3.000e+03 1.053e-04 4.403e-06 110.41° 110.43°
4 4.000e+03 3.314e-05 1.385e-06 151.50° 151.51°
5 5.000e+03 3.090e-04 1.291e-05 -168.70° -168.69°
6 6.000e+03 3.158e-05 1.320e-06 -172.48° -172.47°
7 7.000e+03 1.827e-04 7.636e-06 -169.12° -169.11°
8 8.000e+03 2.179e-05 9.105e-07 -176.08° -176.07°
9 9.000e+03 1.243e-04 5.197e-06 -165.61° -165.60°
Total Harmonic Distortion: 0.002183%
Without load resistor Vas, 1KHz, negative feedback ~51dB
Harmonic Frequency Fourier Normalized Phase Normalized
Number [Hz] Component Component [degree] Phase [deg]
1 1.000e+03 2.448e+01 1.000e+00 -0.01° 0.00°
2 2.000e+03 4.141e-04 1.691e-05 -132.72° -132.71°
3 3.000e+03 3.478e-04 1.421e-05 18.81° 18.82°
4 4.000e+03 3.606e-05 1.473e-06 142.08° 142.09°
5 5.000e+03 8.871e-05 3.623e-06 -136.29° -136.28°
6 6.000e+03 3.272e-05 1.336e-06 -177.84° -177.83°
7 7.000e+03 5.172e-05 2.113e-06 -141.38° -141.37°
8 8.000e+03 2.242e-05 9.159e-07 -179.08° -179.07°
9 9.000e+03 4.241e-05 1.732e-06 -135.88° -135.87°
Total Harmonic Distortion: 0.002266%
1KHz, negative feedback ~33dB (resistor-load Vas) 50Wrms
Harmonic Frequency Fourier Normalized Phase Normalized
Number [Hz] Component Component [degree] Phase [deg]
1 1.000e+03 2.393e+01 1.000e+00 -0.01° 0.00°
2 2.000e+03 3.390e-04 1.417e-05 -140.29° -140.28°
3 3.000e+03 1.053e-04 4.403e-06 110.41° 110.43°
4 4.000e+03 3.314e-05 1.385e-06 151.50° 151.51°
5 5.000e+03 3.090e-04 1.291e-05 -168.70° -168.69°
6 6.000e+03 3.158e-05 1.320e-06 -172.48° -172.47°
7 7.000e+03 1.827e-04 7.636e-06 -169.12° -169.11°
8 8.000e+03 2.179e-05 9.105e-07 -176.08° -176.07°
9 9.000e+03 1.243e-04 5.197e-06 -165.61° -165.60°
Total Harmonic Distortion: 0.002183%
Without load resistor Vas, 1KHz, negative feedback ~51dB
Harmonic Frequency Fourier Normalized Phase Normalized
Number [Hz] Component Component [degree] Phase [deg]
1 1.000e+03 2.448e+01 1.000e+00 -0.01° 0.00°
2 2.000e+03 4.141e-04 1.691e-05 -132.72° -132.71°
3 3.000e+03 3.478e-04 1.421e-05 18.81° 18.82°
4 4.000e+03 3.606e-05 1.473e-06 142.08° 142.09°
5 5.000e+03 8.871e-05 3.623e-06 -136.29° -136.28°
6 6.000e+03 3.272e-05 1.336e-06 -177.84° -177.83°
7 7.000e+03 5.172e-05 2.113e-06 -141.38° -141.37°
8 8.000e+03 2.242e-05 9.159e-07 -179.08° -179.07°
9 9.000e+03 4.241e-05 1.732e-06 -135.88° -135.87°
Total Harmonic Distortion: 0.002266%
PB2, perhaps I should not have brought it up, but you must understand the schematic of the exact IC that I was using. I changed the open loop frequency breakpoint by 100 times, to 10KHz, and in doing that, threw away about 40dB of open loop gain. Yet, with lower open loop gain up to 10KHz, I got lower SMPTE IM distortion at the same output.
What probably happened is that the lower drive impedance, from 100meg ohm to 1 meg ohm, optimized the drive impedance for the output stage.
What probably happened is that the lower drive impedance, from 100meg ohm to 1 meg ohm, optimized the drive impedance for the output stage.
andy_c said:
Hi Andy,
You raise a great question when wondering if my PIM analyzer can be duplicated in simulation. I think the answer is yes.
Figure 3 in my PIM paper shows a block diagram of the complete analyzer, which I referred to as a Coherent IM Analyzer. It uses coherent detection in quadrature to extract both conventional SMPTE IM (AIM) and PIM.
The heart of the analyzer is a state variable voltage controlled oscillator that provides outputs at 0 degrees and 90 degrees. These sinewaves at the 6 kHz “carrier” frequency drive a pair of phase detectors in quadrature. One of these is the phase detector and is used to complete the phase-locked loop. The output of the PLL is phase locked to the 6 kHz carrier. The PLL has very low bandwidth so that it does not track short-term phase variations in the signal it receives. The synchronously demodulated output of the phase detector is PIM, while the synchronously demodulated output of the synchronous AM detector is AIM.
The coherent IM analyzer was actually built as a modified version of my THD analyzer prototype by converting the state variable tracking notch filter of the THD analyzer into the state variable VCO. The in-phase and quadrature detectors were already part of the THD analyzer for the auto-null function.
One way to simulate the functionality of the Coherent IM Analyzer is to avoid the use of the PLL and just use quadrature versions of the known 6 kHz source carrier to drive simulated multipliers that act as synchronous detectors. The other input to these multipliers is the output of the amplifier under test, with the 60 Hz signal component removed by a high-pass filter.
The outputs of the multipliers can be analyzed by FFT to view the demodulated components at 60 Hz and its harmonics, both in the amplitude domain and the phase domain. Alternatively, the outputs of the demodulators (multipliers) could be passed through simulated low-pass filters (just as in my coherent IM analyzer) to view the real-time AIM and PIM residuals.
The simulation would start with three signal sources. One 60 Hz source and two 6 kHz sources that are 90 degrees out of phase. The 60 Hz source and one of the 6 kHz sources would be mixed in the ratio 4:1 to provide the test signal to the amplifier under test.
The two 6 kHz sources would be mixed in controlled proportions to produce two signals 90 degrees out of phase whose absolute phase can be controlled by the mixing proportions so that one of them is exactly in phase with the 6 kHz carrier coming out of the AUT. This amounts to a manual duplication of the PLL function. These two quadrature signals are then used to drive simulated multipliers to form the in-phase and quadrature coherent detectors. The absolute phase of the quadrature pair applied to the detectors can be adjusted so that the DC component out of the in-phase detector is zero when the 60 Hz signal is not applied.
I’m sure there are other approaches available as well for simulating the functionality of my Coherent IM Analyzer.
Cheers,
Bob
Look here, for how to do two-tone 1:1 IMD sims:Rafael.luc said:
http://www.diyaudio.com/forums/showthread.php?postid=1349571#post1349571
- Klaus