Times have changed and all the functions are freely available both in Python and MATLAB with external libraries.
NTK's code use python for the whole thing which is already done, no need to reinvent the wheel for anyone else unless they want to.
https://www.audiosciencereview.com/...hematics-and-everything-else.9970/post-352067
Klippel's documentation shows an error rate which is dependent on the number of fitting points related to the expansion number N. -20dB or more is meant to be good enough.
The number of measurement points necessary to reach the expansion order is given by: 1.5 * 2*(N+1)^2
This is how I came up with the figure of aiming for N=5, 185 points or more to reduce the fitting error to below -20dB for 1K.
That graph is showing exactly what I predicted, for higher frequencies the whole idea doesn't work.
They also just still use a stitching method as well, because it seems that for lower frequencies the method also doesn't work well anymore.
Leaving a small usable range left from just 60Hz to about 1kHz.
The question remains what method will give less error from 200Hz and upward?
Especially in combination with near-field measurements.
It also very clearly shows that there aren't many benefits for a generic 2-way bookshelf speaker.
In that case, all resonances are far to high and the low end is totally predictable.
All of this was already predicted by multiple people who have been doing this for years 😉😎
They also just still use a stitching method as well, because it seems that for lower frequencies the method also doesn't work well anymore.
Leaving a small usable range left from just 60Hz to about 1kHz.
The question remains what method will give less error from 200Hz and upward?
Especially in combination with near-field measurements.
It also very clearly shows that there aren't many benefits for a generic 2-way bookshelf speaker.
In that case, all resonances are far to high and the low end is totally predictable.
All of this was already predicted by multiple people who have been doing this for years 😉😎
What do you mean by "phase matched"?
I guess this somehow relates to the time relation(s) of the outgoing and incoming waves. Even a cheap microphone will provide this time information with good accuracy and precision.
I guess that should be expected that these functions would be available by now. I am way out of date and have no experience with Python or MATLAB, but I have a lot of experience with implementations of the ideas. There are several "gotcha's" that occur with the numerical parts.
I have no idea where this equation comes from and I don't see how it could be true.
If I want to find the radiation contribution values for 20 modes (unknowns), then I need only 20 data points (knowns) to uniquely determine the unknowns (all complex.) I found that for horizontal only, 20 modes was overkill and that 12-15 worked very well. This makes the above equation look absurd.
Remember that we are taking data in the near field and as such one cannot just calculate the impulse response and let it go from there. You have to move the results into the far field which is why the full blown analysis of the radiation modes is required at all frequencies and not just below some "matching" point.
This is because of the numerical issues that I talked about. The system is becoming "singular" and one needs to use some tricks - like SVD - to get stable results, but yes, things become less reliable at LFs.
Since we need the complex values for the unknowns we need to have the complex values for the knows accurately. If the phases for sets of measurements are not consistent then the results will be in error.
NOt if the phases don't track well.
I still don't get it. The microphone output is a real valued voltage as a function of time.
What is the meaning of "phase matched" or "phase tracking" in this context?
What is the meaning of "phase matched" or "phase tracking" in this context?
The explanation from Klippel is in this document on page 25, there are further explanations of the error metrics
https://www.klippel.de/fileadmin/kl...nsparancies/Klippel_holografic processing.pdf
Also on page 14 there is acknowlegement that in theory the directivity can be described by a very few points, which is perhaps what you are saying.
I don't have the ability to discuss whether what Klippel or you say is correct. I have no reason to doubt either, most likely both are right for different reasons.
I guess meaning that the phase has a proper reference for all channels?
As soon as that shifts or so, you will get artifacts.
I simply don't get what everyone means by "phase" in this context. The term "phase" relates to the angular argument of a sine (or cosine) function.
However, as I see it, the microphone(s) will record the test signals from the speaker and its room echoes. The signals can be Dirac pulses, white or pink noise, MLS, sweeps, etc. They will not be sinusoidal.
However, as I see it, the microphone(s) will record the test signals from the speaker and its room echoes. The signals can be Dirac pulses, white or pink noise, MLS, sweeps, etc. They will not be sinusoidal.
I think this is not clear to many people at first, it certainly wasn't to me.
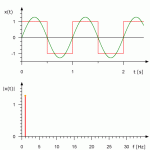
In brief, it's a consequence of the Fourier transform, that takes real values as a function of time, and transforms that into amplitudes and phases as a function of frequency.
There are other transforms with similar behaviour and you can consider it a mathematical artefact but Nobel laureate R. Penrose thinks it is deep that so many real valued problems seem to work out mysteriously well once transformed to the complex plane. His discussion of this in the book "The Road to Reality" I found very helpful.
Best wishes
David.
Last edited:
Any signal can be constructed from a sum of sinusoidal signals with for every frequency a certain amplitude and phase.
Please enlarge to show animation.
One of the patent claims is to use the data after the time window, that is normally discarded, to estimate the reflections.
That seems clever, use the data more completely.
I don't remember the details because it's been a while since I looked closely at the patent, but that's the basic idea IIRC.
Best wishes
David
Sure. But this has nothing to do with the microphones.
I wrote before, microphones provide a real-valued, time-dependent voltage signal that reflects the sound pressure vs. time. Microphones do not provide the Fourier sine/cosine coefficients as amplitude and phase. That's why I don't understand the meaning of "phase tracking" or "phase matched" microphones. These terms seem like nonsense to me, but I am sure there is some proper idea behind these statements, and I'd like to understand.
Just as an example: assume a loudspeaker in an anechoic environment. The loudspeaker emits a test signal at time t = 0 s, and this signal is recorded by two microphones. Both microphones are placed on the same axis, one at 5 m distance from the loudspeaker, the other at 6 m distance. The speed of sound is 340 m/s, so the first microphone sees the signal at time t = 14.7 ms, and the second microphone sees it with a delay of 2.9 ms at t = 17.6 ms.
This has nothing to do with Fourier transforms and phase.
A pressure as a function of time is equivalent to a amplitude and phase as a function of frequency. One is in the time domain, the other is in the frequency domain. Both contain the same information.
It's like a different language. An English newspaper and a French newspaper both have an accurate story on an event. Someone says the event took place at an 'eglise'. You say the word 'eglise' isn't an English word.
That's true, but 'eglise' means 'church' which is an English word and that is present in the English newspaper story and where the event took place.
Phase = 2 x pi x f x t
It's like a different language. An English newspaper and a French newspaper both have an accurate story on an event. Someone says the event took place at an 'eglise'. You say the word 'eglise' isn't an English word.
That's true, but 'eglise' means 'church' which is an English word and that is present in the English newspaper story and where the event took place.
Phase = 2 x pi x f x t
In most cases, people mean either the ADC/DAC or even just the software drivers.
Since the exact latency isn't fixed.
(And since windows 8/10/11 seems to be all over the place)
Point is that the signals need a time reference when getting out (playback) and getting in (record).
Any discrepancies show in the (relative) phase, which is why people call it a phase problem.
Even just analog devices like microphones have some circuitry in them with some basic high pass/low pass filtering.
The values can depend on the brand/model, but there are also tolerances (up to well over 10%).
This will also add some additional group delay as well.
Edit: even not every electret capsule is the same. Since freq response and phase are tight together, any differences in that respect would or could also give any time differences (aka phase differences)
First toys have arrived!
That's already more commitment than with arta_tic, which I developed without the tic board and stepper motor.
That's already more commitment than with arta_tic, which I developed without the tic board and stepper motor.
Sure. But the phase is a property of the Fourier coefficients of a specific signal. It's not a property of the microphone. I therefore don't see how microphones can be "phase matched" or "phase tracking".
Ok, that makes more sense. The latency of the sound processing is indeed important (but that's something else than phase). I have never worried about Windows, but I am sure there are ways to get a grip at the audio latency. With Linux and macOS I never had any issues with reproducible timing of the recorded data. Repeated measurements are usually consistent to within the time resolution determined by the sampling rate.
Also, so-called "USB microphones" need not apply here.
I didn't think of the transfer function of the microphones. I simply tend to think that the data recorded from the microphone is already compensated for the specific transfer function(s) of the microphone(s). MATAA does that on the fly, so I usually don't spend a lot of time thinking about this. The MATAA method is to determine the phase-frequency response from the amplitude-frequency response, then compensate for both in the frequency / Fourier domain.
Maybe the question is: can differences in microphone transfer function be compensated in software for this application?
To use sound pressure as an analogy, if a microphone has an amplitude response that rises with frequency, it will incorrectly report the level of high frequency of the sound field that it is in. Then if we want to average its output with another microphone that itself has a different amplitude response, the average of the two will always be wrong when compared to the actual sound field. Now, in that example, we can compare those microphones to a reference and produce a software correction to compensate for the error in amplitude response. But can a software correction be made for the phase response of a microphone? I don't know. Commercial sound intensity probes use matching microphone capsules rather than software correction (as far as I am aware), but their designers may have reasons behind that decision that are irrelevant for this application. And given that the phase response of a microphone is closely tied to its frequency response, maybe it can.
To use sound pressure as an analogy, if a microphone has an amplitude response that rises with frequency, it will incorrectly report the level of high frequency of the sound field that it is in. Then if we want to average its output with another microphone that itself has a different amplitude response, the average of the two will always be wrong when compared to the actual sound field. Now, in that example, we can compare those microphones to a reference and produce a software correction to compensate for the error in amplitude response. But can a software correction be made for the phase response of a microphone? I don't know. Commercial sound intensity probes use matching microphone capsules rather than software correction (as far as I am aware), but their designers may have reasons behind that decision that are irrelevant for this application. And given that the phase response of a microphone is closely tied to its frequency response, maybe it can.