John Curl's Blowtorch preamplifier

[Edmond Stuart]

.......... Too much extra info.

That's the price of being famous 🙂

 

[PMA]

result fo bipolars:

 

[john curl]

The bipolar result looks OK, but the fet example is confusing. That is WHY I wanted to start with an IDEAL FET first.

 

[PMA]

I do not know if this is better, generic N-JFET devices:

 

[john curl]

I don't seem to understand how you can get 3rd harmonic distortion from a single idealized square law device. The problem is that the 3'rd harmonic distortion that is inherent in most fets will confuse the comparison between single ended and diff pair comparison, because of the POLARITY of the 3'rd harmonic and the potential subtraction of the inherent 3'rd harmonic in the device and the 3'rd harmonic formed by the 2'd harmonic when a differential pair is made. If they add, then we get the wrong result, if they subtract, we might even get a 0 result. Both are wrong, but the 0 result, might be one of the factors that Nelson Pass has seen, or something akin to it.
First, we need the exact mathematical expressions, put in such a way as we can compare an ideal fet, both single ended and differential.
The result with the differential vs single ended bipolar is clear, and we can discuss it now, if it would be useful, but the fet solution should be more interesting, overall.

 

[PMA]

I understand, the case is that I have not used the "ideal" square law device. Someone has to do it by modelling in spice, if willing to do so.

 

[john curl]

Dr. Pederson implied that the original Spice model for a fet is ideal.

 

[PMA]

Maybe I got it. Rd must be minimized almost to zero and drain currents to be plotted:

 

[PMA]

Now I have really only 2nd, even in a large scale:

 

[syn08]

I don't seem to understand how you can get 3rd harmonic distortion from a single idealized square law device.

John,

Sorry for my ugly handwriting.

There's nothing magic in this 2nd harmonic for single FET vs. 3rd harmonic for diff FET pair. Think qualitatively it in the following way:

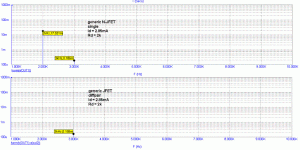
a) As you said, a single FET device follows a square law dependency of Id vs. Vgs. This dependency is an "even" function of Vgs, that is, Id(-Vgs)=Id(Vgs). Look at http://en.wikipedia.org/wiki/Even_function under Harmonics. An even function will generate in the frequency domain only even harmonics (2nd, 4th, etc...).

b) For the differential pair of FETs, look at Andy's current equation of Id vs. Vgs. This function is now an "odd" function, that is, Id(-Vgs)=-Id(Vgs). See again the above reference. Odd functions generate in the frequency domain only odd harmonics (3rd, 5th, etc...).

Bipolars do not have the same behaviour, their Ic(Vbe) is exponential, which is not an even or odd function. The Taylor expansion will have both even and odd power terms. Therefore, bipolars will have even and odd harmonics both in singles and in a diff pair.

If you want any quantitative evaluation, then you have to follow my calculations (and my ugly handwriting) above. If there's any specific value/ratio that you would like to compare between the single JFET and the diff pair, just let me know I'll see what I can do.

 

[john curl]

Please, just generate the equations.

 

[Nelson Pass]

I don't seem to understand how you can get 3rd harmonic distortion from a single idealized square law device.

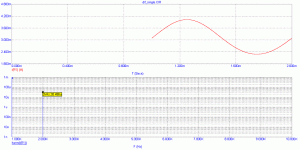
My experience is that this is very much a function of Vds variation.
I'm assuming that if you were to operate the device at constant
Vds you would see a more pure square law. Am I mistaken
on this?

 

[john curl]

I am not as simple as my statement seemed to imply. However, I still need exact equations, if we are to discuss anything in detail.

 

[syn08]

Please, just generate the equations.

I'm afraid you have to be a little more specific. Which equations? You already have the FET diff pair spectral response in my previous message. If it's my handwriting that you have a problem with, then just ask questions. Or even better, grab a pen and follow through some algebra and trigonometry calculations.

 

[john curl]

Sorry, I will look again and see if it is in a useful form enough to go forward.

 

[PMA]

My experience is that this is very much a function of Vds variation.
I'm assuming that if you were to operate the device at constant
Vds you would see a more pure square law. Am I mistaken
on this?

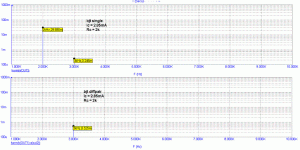
This is completely confirmed by simulation in

http://www.diyaudio.com/forums/showthread.php?postid=1477363#post1477363

for almost zero Rd (Vds constant), where there is only 2nd harmonic, and previous simulations for resistor load, where we have Vds variation, and 3rd and higher harmonics.

 

[Nelson Pass]

Thanks. Always comforting to see measurement confirmed by
simulation. 😉

 

[Edmond Stuart]

[snip]
Bipolars do not have the same behaviour, their Ic(Vbe) is exponential, which is not an even or odd function. The Taylor expansion will have both even and odd power terms. Therefore, bipolars will have even and odd harmonics both in singles and in a diff pair.
[snip]

bipolars will have even harmonics ...... in a diff pair
No! Any (perfectly) symmetrical circuit will only produce odd harmonics.

edit: Oops, that too is not true. I mean: cannot produce even harmonics.

 

[andy_c]

This is completely confirmed by simulation in

http://www.diyaudio.com/forums/showthread.php?postid=1477363#post1477363

for almost zero Rd (Vds constant), where there is only 2nd harmonic, and previous simulations for resistor load, where we have Vds variation, and 3rd and higher harmonics.

Hi Pavel,

If you set LAMBDA=0 in the JFET model, this should also force pure square law behavior even as Vds varies - as long as Vds does not get so small that the FET goes into the triode region. This might be convenient for some simulations.

 

[john curl]

Even with all the interference and conjecture, we are still not at the end. I hope that we can get there. Measurements only confuse this issue at this point. I need hard, accurate equations. Then we can insert more realistic devices, and note what happens. Finally, we can compare measurements with prediction.