John Curl's Blowtorch preamplifier part II

[KBK]

Pardon the barging in, thought some of you might like to see this, if you haven't already.


diamond based wide gap 'deep depletion' mosfets.

Diamond is largely recognized as the most ideal material in WBG development, owing to its superior physical properties, which allow devices to operate at much higher temperatures, voltages and frequencies, with reduced semiconductor losses.

A main challenge, however, in realizing the full potential of diamond in an important type of FET—namely, metal-oxide-semiconductor field-effect transistors (MOSFETs)—is the ability to increase the hole channel carrier mobility. This mobility, related to the ease with which current flows, is essential for the on-state current of MOSFETs.

Researchers from France, the United Kingdom and Japan incorporate a new approach to solve this problem by using the deep-depletion regime of bulk-boron-doped diamond MOSFETs. The new proof of concept enables the production of simple diamond MOSFET structures from single boron-doped epilayer stacks. This new method, specific to WBG semiconductors, increases the mobility by an order of magnitude. The results are published this week in Applied Physics Letters.

In a typical MOSFET structure, an oxide layer and then a metal gate are formed on top of a semiconductor, which in this case is diamond. By applying a voltage to the metal gate, the carrier density, and hence the conductivity, of the diamond region just under the gate, the channel, can be changed dramatically. The ability to use this electric "field-effect" to control the channel conductivity and switch MOSFETS from conducting (on-state) to highly insulating (off-state) drives their use in power control applications. Many of the diamond MOSFETs demonstrated to date rely on a hydrogen-terminated diamond surface to transfer positively charged carriers, known as holes, into the channel. More recently, operation of oxygen terminated diamond MOS structures in an inversion regime, similar to the common mode of operation of silicon MOSFETS, has been demonstrated. The on-state current of a MOSFET is strongly dependent on the channel mobility and in many of these MOSFET designs, the mobility is sensitive to roughness and defect states at the oxide diamond interface where unwanted carrier scattering occurs.

To address this issue, the researchers explored a different mode of operation, the deep-depletion concept. To build their MOSFET, the researchers deposited a layer of aluminum oxide (Al2O3) at 380 degrees Celsius over an oxygen-terminated thick diamond epitaxial layer. They created holes in the diamond layer by incorporating boron atoms into the layer. Boron has one less valence electron than carbon, so including it leaves a missing electron which acts like the addition of a positive charge, or hole. The bulk epilayer functioned as a thick conducting hole channel. The transistor was switched from the on-state to the off-state by application of a voltage which repelled and depleted the holes—the deep depletion region. In silicon-based transistors, this voltage would have also resulted in formation of an inversion layer and the transistor would not have turned off. The authors were able to demonstrate that the unique properties of diamond, and in particular the large band gap, suppressed formation of the inversion layer allowing operation in the deep depletion regime.

 

[gpapag]

Daniel, thanks.
I have already have done some work.

Using Steinberg Wavelab:
I generated a 997Hz sinusoidal tone at –60dBFS and recorded a 30sec file , saved as 32bit float/44100Hz.

1 32 bit float
Dropbox - 1 32bit float.wav

Then this file was used to generate the following files:

2 No dither. Saved as 16 bit
Dropbox - 2 no dither saved as 16bit.wav

3 No dither. Saved as 16 bit. Then dithered using Intern dither, noise type Off
Dropbox - 3 no dither saved as 16bit then Int dith-noise type Off.wav

4 No dither. Saved as 16 bit. Then dithered using Intern dither, noise type 1
Dropbox - 4 no dither saved as 16bit then Int dith-noise type 1.wav

5 No dither. Saved as 16 bit. Then dithered using Intern dither, noise type 2
Dropbox - 5 no dither saved as 16bit then Int dith-noise type 2.wav

6 Dithered using Intern dither, noise type Off. Then saved as 16bit
https://www.dropbox.com/s/u2n9rhoszs4k2b9/6 Int dith-noise type Off then saved as 16bit.wav?dl=0

7 Dithered using Intern dither, noise type 1. Then saved as 16bit
https://www.dropbox.com/s/c6z7y6qk179ioj2/7 Int dith-noise type 1 then saved as 16bit.wav?dl=0

8 Dithered using Intern dither, noise type 2. Then saved as 16bit
https://www.dropbox.com/s/dk7d6yl0y4fv4ab/8 Int dith-noise type 2 then saved as 16bit.wav?dl=0

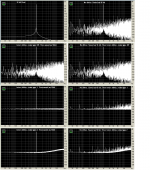
Attached are the FFT spectrums of these files
RMAA 6.4.1. (65536 samples, zero padding none, FFT overlap 75%, Window Kaizer beta 9)

George

 

[jan.didden]

Jan, Waly, the question George is answering isn't necessarily what the mathematical function *should* be doing (applying dither 1.5 bits above the new bit depth regardless of whether the truncation has/hasn't happened) but what the software is actually doing.

That's to answer the question: "dither then truncate" or "truncate then dither"? The mathematical answer should be "doesn't matter", unless it's using an algorithm that borrows data from the higher resolution to inform it's dither algorithm (and thus not totally de-correlated from the input stream) to perceptual mask the noise shaping. I don't know any dither that does that, though.

If I'm mistaken as to your point, George, my apologies.

OK, maybe I am missing the point. I was talking about the effect on the signal, not what happens if you do 'something' to it with algorithms afterward.

The way I see it: if I dither a 24 bit word, I am 'manipulating' the lower bit(s), right?

If I then truncate the 8 lower bits so I have only the upper 16 left, does that then not mean that I have lost whatever the dithering did?

Jan

 

[DPH]

George -- clearly the processing is very different pre/post truncation. So definitely with Steinberg, dither first. Edit -- thanks for providing these files!

Jan -- from a mathematical perspective of the signal processing I don't think you're getting any argument! Just simply the implementation of said processing, at least in this software's case, isn't doing the same sort of manipulation on the 15th and 16th bits when given these two different inputs.

 

[DPH]

Exactly. Some of the commercial audio dither algorithms are proprietary. Some audio processing programs don't expose their dithered audio unless they do the tuncation first, perhaps to make reverse engineering of their dither algorithm more difficult.

Looking into some non-subtractive dither AES and IEEE articles, it looks like dither prior to quantization is virtually always assumed and even dictated, but often it is in the context of A/D conversion where the exact transfer function of the data converter may result in less total or less objectionable errors if dither is added first, which might be a purely practical consideration, aside from basic theory. Perhaps not something applicable for truncation.

...

But, I suspect that's not what they're doing. Perhaps along the lines of Daniel's point about manipulating lower bits. If so, presumably testing has shown it to sound better than conventional dither.

I'm completely not suspecting a superiority of one method or another (if it is, great, and it must be totally from doing some sort of correlated dither). I'm totally suspecting that they coded it in one fashion and not another (Steinberg clearly built their pipeline in one way and one way only), and we're seeing the effects of that. My curiosity of the manipulation of 17-24 was to tease out information about the data processing algorithm.

 

[PMA]

Jan is right.

 

[scott wurcer]

OK, maybe I am missing the point. I was talking about the effect on the signal, not what happens if you do 'something' to it with algorithms afterward.

The way I see it: if I dither a 24 bit word, I am 'manipulating' the lower bit(s), right?

Jan

Jan you're missing a not so subtle point, going 24bit to 16bit the TPDF function's magnitude is in 16bit LSB's not 24. The noise floor for any type of dither is computable in the simplest case of TPDF it is slightly more than the 16bit quantization noise so you must raise the noise floor of the 24bit file to that. BTW when creating pure mathematical examples sometimes the ceil() and floor() functions for rounding give very slight differences. This animation is not bad YouTube

As for George's plots only the two with flat noise floors are proper applications of dither. The others are flawed some quite obviously with a couple obviously doing nothing.

 

[keantoken]

How much justification is there for "shaped" dithers or is plain flat dither almost always ideal?

 

[DPH]

Kean, worth visiting Homepage of Alexey Lukin and see how the 8 bit samples sound yourself! (realizing, of course the magnitude of difference)

 

[Markw4]

Jan: If you add dither intended for reducing a 24-bit file to a 16-bit file, the dither noise will be added to bits 16 and 15, not bits 24 and 23. Therefore, the dither noise should remain after truncation to 16-bits.

In recording programs they refer to that type of dither as 16-bit. There may also be other dithering options available, such as 24-bit or 20-bit that would add noise to bits 24 and 23, or bits 20 and 19, respectively.

That is, such would be the case if the dither were according to basic mathematical theory. Apparently, some commercial dithering processes may work in a somewhat different fashion, with Steinberg UV-22 being one example. In fact, some people have argued UV-22 should not even be called dither because it reportedly adds a low level 22kHz signal, not random noise.

 

[jcx]

add dither noise at the level you intend to truncate at to "whiten" the quatntization noise from the following truncation step

and the order definitely matters, truncation is a nonlinear operation and dosen't "commute" with the dither noise addition step

proper application of dither doesn't just "mask" the quantization noise correlation with the signal (the modulated hissy, spitting sound of musical note fades) it destroys the correlation altogether (up to the 2nd statistical moment anyway seems to be enough for hearing)

 

[scott wurcer]

it destroys the correlation altogether (up to the 2nd statistical moment anyway seems to be enough for hearing)

Easily demonstrable by separating afterwards.

 

[Destroyer OS]

As I answered before I haven't done this. But Steve Hoffman did:

Quoted from Here <snip>

So it's not just me... Awesome. Thanks, this is gold.

 

[Waly]

add dither noise at the level you intend to truncate at to "whiten" the quatntization noise from the following truncation step

and the order definitely matters, truncation is a nonlinear operation and dosen't "commute" with the dither noise addition step

proper application of dither doesn't just "mask" the quantization noise correlation with the signal (the modulated hissy, spitting sound of musical note fades) it destroys the correlation altogether (up to the 2nd statistical moment anyway seems to be enough for hearing)

Truncating is indeed a nonlinear quantization operation, and it can be modelled as the summation of the signal with a noise source *). Dithering has exactly the role of linearizing, and the linearizing effect should be the same if you apply it before or after the truncation (on the 1.5bit LSB of the 16bit output). The audibility of pre- and post- truncation dithering is very unlikely, and I suspect if the sequence is long enough the spectra will also mathematically match. I'll do some math, time permitting, but as long as the dithering data is not correlated with the signal, I don't see any reason why they should be different (actually, converge).

*) L. B. Jackson, "On the interaction of round off noise and dynamic range in digital filters," The Bell System Technical Journal, vol. 49, no. 2, pp. 159-184, Feb. 1970.

 

[Markw4]

There is a paper here of possible interest: AES E-Library >> Resolution Below the Least Significant Bit in Digital Systems with Dither
if someone has access. Don't see how one can get sub-LSB resolution without correlation. Or to put it another way, don't see how to get sub-LSB resolution if dither is applied after truncation. Am I missing something?

 

[DPH]

Be a little more careful interpreting this statement:

Expanding on previous arguments, it is shown that this is not true when the signal to be quantized contains a wide-band noise dither with an amplitude of approximately the step size.

E.g. 15th/16th bit dither will allow signal in the 15th/16th bit to emerge.

 

[rayma]

There is a paper here of possible interest: AES E-Library >> Resolution Below the Least Significant Bit in Digital Systems with Dither
if someone has access. Don't see how one can get sub-LSB resolution without correlation. Or to put it another way,
don't see how to get sub-LSB resolution if dither is applied after truncation. Am I missing something?

This is a famous paper. http://www.drewdaniels.com/dither.pdf

 

[gpapag]

Here is a video which shows what Scott is talking about dither application bit level
YouTube
The software used in the video is ProTools .The dither plugin is Ozone.

To quote (for keantoken who asked the question):

"Like other dither manufacturers, we're selling you noise. Even more difficult, we're selling you noise that you can barely hear, and in the case of some shaping algorithms (psychoacoustic ones) we're telling you not to turn up the level so you can even really evaluate it. All of this would make it pretty frustrating as a user to try to get a handle on whether any of this makes a difference, or if we're all just packaging up random noise and calling it a digital audio breakthrough."

http://downloads.izotope.com/guides/izotope-dithering-with-ozone.pdf

link to sample audio files used in the Ozone guide:
http://downloads.izotope.com/guides/izotope-dithering-with-ozone-files.zip

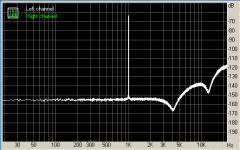
PS. Attached is the FFT spectrum of what Audacity does to the 32bit float file when it exports it (there is no discrete dither application step) as "WAV signed 16bit PCM"

George

 

[billshurv]

The MASTER TAPE and the RECORD sounded the practically the same. We honestly couldn't tell one from the other during playback. This was of course playing back the tape on the master recorder with the mastering "moves" turned on. The acetate record was played back flat on the AcousTech lathe with the SAE arm and Shure V15 through the Neumann playback preamp (as seen in so many pictures posted here of AcousTech).

And this is the thing I have a real problem with. Unless you have an exceedingly well damped setup it's trivial to measure the FM effects of arm/cartridge resonance. It makes no sense for the lacquer playback to sound closer to the master tape than the digital rip unless there is a healthy expectation bias or something badly wrong with some of the equipment.

 

[morinix]

.....or something badly wrong with some of the equipment.

At one of the best mastering facilities in the world? Read what I quoted in your post and go read some reviews of Kevin Gray's work.