Re required port surface area for a given speaker: ports at large signals can and will suffer from harmonic distortion, noise, and compression. You'd have to define what goals you want to reach for each problem area - how low do you want distortion to be at full signal, how low noise, how low compression? Because they'll never be 0.
From the conclusion of "Maximizing performance from loudspeaker ports", Salvatti, Button - imo they say it best:
There's also all kinds of m/s values floating around. In the aforementioned paper, <10 m/s is thrown into the ring. Small afair stated an acceptable value of 15-20 m/s. My personal experience falls somewhere in the middle of that. But to each their own.
From the conclusion of "Maximizing performance from loudspeaker ports", Salvatti, Button - imo they say it best:
Vast historical data and results herein suggest that the largest port area allowable by your design should be employed to keep air velocity down if low port compression and low distortion are desired.
There's also all kinds of m/s values floating around. In the aforementioned paper, <10 m/s is thrown into the ring. Small afair stated an acceptable value of 15-20 m/s. My personal experience falls somewhere in the middle of that. But to each their own.
The interesting discovery in the respective papers and in the experiments shown in this thread (at least for me) was that airspeed is not that relevant by itself. It's the air displacement at the port terminations that matters.There's also all kinds of m/s values floating around.
Airspeed in the central section of the port can be huge and still pose no problem.
Yes. I actually think I will agree with this.The interesting discovery in the respective papers and in the experiments shown in this thread (at least for me) was that airspeed is not that relevant by itself. It's the air displacement at the port terminations that matters.
Airspeed in the central section of the port can be huge and still pose no problem.
It's in fact almost worth putting it a bit more officially out there. 👍🏻
On the other hand, lower air velocity is always better in all cases.
But yes I am mostly curious to see how this will change certain things on a more practical level.
Because it could mean a smaller diameter and port length would be sufficient.
Meaning we're pushing that port resonance further up!
Definitely! Make the port (terminations) as big as possible.On the other hand, lower air velocity is always better in all cases.
That's the main benefit and one of the goals developed in this thread.Meaning we're pushing that port resonance further up!
In fact the initial idea (and thread title) of resonance absorbers turned out to be less important once the port geometry was optimized!
Another benefit of a narrow center section is to attenuate enclosure resonances as much as possible.
😊It's in fact almost worth putting it a bit more officially out there.
Thanks, I appreciate your encouragement!
I still would like to confirm the results with a higher spl 12" driver ...
Last edited:
The interesting discovery in the respective papers and in the experiments shown in this thread (at least for me) was that airspeed is not that relevant by itself. It's the air displacement at the port terminations that matters.
Airspeed in the central section of the port can be huge and still pose no problem.
Correct, the pioneers recommended Av = Sd for a baffle thickness vent, so when larger was needed a simple slant panel parabolic horn was added where St = Sd, so similar using round, square, rectangular tubes + the needed flare works great as Danley did in at least one of his consumer? designs.
Muffler adapter design I used as a guide: pg. 838, Fig.10 (Note the 'powerhouse' authors)
In terms of the UI would it be possible to include a note to guide the user that the strouhal number should ideally be used to define the port exits size and not the port central / minimum size?
It will be clear from the chart heading that the Strouhal number applies to the port outlet.
(Hornresp assumes that the port tube is a cylindrical pipe).
The interesting discovery in the respective papers and in the experiments shown in this thread (at least for me) was that airspeed is not that relevant by itself. It's the air displacement at the port terminations that matters.
Airspeed in the central section of the port can be huge and still pose no problem.
Any recommended air velocity numbers cited anywhere would be for non-tapered ports, in which the air velocity would be relatively constant. I suppose you could calculate / simulate max. air speeds in flared ports with AKABAK, COMSOL or the like, but who, especially in the non-commercial space, has ever done that?
I must say though I was surprised how small the bottleneck of a flared port can be to still work well. Both via third party discoveries, like the aforementioned AES paper, as well as in my own tests. For example, as some here might know, I did the most extensive public review of the L'Acoustics KS28, including extracting the chassis and testing / comparing it in an enclosure with a 1/2 sd sized normal straight port with the same tuning. The L'Acoustics "L-Vent" is only 1/4 sd large at its bottleneck, meaning half the area, and yet performed similarly. It still had portnoise however 🙂 - not less than the straight port.
Props for the thread. I only recently stumbled across it, on a research on port absorbers, within the development of a fullrange BR box with large port, and it helped me quite a bit.
Particle displacement = V / (2 * pi * f)
It should probably be noted that this equation is appropriate for small velocities (= absence of turbulence), when we can assume that the system is linear, so we can describe the oscillations by a harmonic law. In the presence of turbulence, this ratio will give some error.
Last edited:
All of these kinds of equations are only ever valid in linear systems and conditions.It should probably be noted that this equation is appropriate for small velocities (= absence of turbulence), when we can assume that the system is linear, so we can describe the oscillations by a harmonic law. In the presence of turbulence, this ratio will give some error.
So to me it sounds a bit obvious.
But yes it's a valid point nevertheless. 🙂
No, it's still not entirely obvious to me 🙂. I opened to read the Fluid Dynamics by Landau and Lifshitz (2nd. ed., p1) , and that's what it says there

That is, hydrodynamics equations operates with velocity distributions (v in the notation by Landau and Lifshitz) in space rather than velocities of particular particles(u in the notation by Landau and Lifshitz). Whereas the Strouhal number is defined through the mean flow velocity u rather than v. So, probably David's redifinition of Strouhal number through the mean particle displacement is quite correct in a wider range of u. Sorry for the perturbation of the thread, it's just important to clarify for myself the physics behind equations 🙂.
That is, hydrodynamics equations operates with velocity distributions (v in the notation by Landau and Lifshitz) in space rather than velocities of particular particles(u in the notation by Landau and Lifshitz). Whereas the Strouhal number is defined through the mean flow velocity u rather than v. So, probably David's redifinition of Strouhal number through the mean particle displacement is quite correct in a wider range of u. Sorry for the perturbation of the thread, it's just important to clarify for myself the physics behind equations 🙂.
Last edited:
I agree with you, but it's not too difficult for ports that are mostly designed by a simple radius such as the 'NFR' ports in the Harmon papers (IIRC). Most ports can be approximated similarly even if they have an additional radius at the very end.That's a bit tricky, because how do you define exit diameter with some totally random flare, chamfer or round over?
Stil, my overall point was only that it would help less knowledgeable designers to note that parameters of flared ends are far more important than the central section, in contrast to the common reliance of max. air speed.
Speaking of which, I think it's still mainly just the entrance and exit flare that is most important?In fact the initial idea (and thread title) of resonance absorbers turned out to be less important once the port geometry was optimized!
Meaning that the middle section can just be done with a straight tube to get results that are similar?
Yeah, my idea was mostly coming from a theoretical point of view.I agree with you, but it's not too difficult for ports that are mostly designed by a simple radius such as the 'NFR' ports in the Harmon papers (IIRC). Most ports can be approximated similarly even if they have an additional radius at the very end.
Stil, my overall point was only that it would help less knowledgeable designers to note that parameters of flared ends are far more important than the central section, in contrast to the common reliance of max. air speed.
I rarely buy of the shelf port to begin with and just use PVC tubing with a round-over on the baffle as well as inside the cabinet (entrance).
That round-over on itself is not very well defined, and mostly depends on thickness of the wood, diameter of the port etc etc.
So yes, it's a simple radius, but also one that is not really defined.
It probably doesn't matter that much with a small amount of end-correction, but it's good to investigate that as well as to keep it in mind 🙂
Probably, but to maximise the flares and the entrance/exit diameter without exceeding the flare rate around 30° (see #526) it makes sense to keep the central length as short as possible.that the middle section can just be done with a straight tube to get results that are similar
I'll try to show that in the next update.
I understand, I am just thinking a bit more practically.Probably, but to maximise the flares and the entrance/exit diameter without exceeding the flare rate around 30° (see #526) it makes sense to keep the central length as short as possible.
I'll try to show that in the next update.
It's just a bit easier to have a straight tube in the middle to be able to tune, or make different lengths.
In that case we only have to print out the port ends (flares) and not just an entire port every time,
Printing only the ends is also a much easier printing proces. 🙂
I think the impact in absolute performance won't be that big?
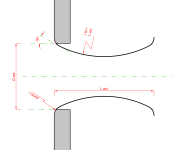
Simple Excel sheet for calculating a flared port with NFR=0,5
I used basic geometry and the formulas by salvatti/devantier/button and set up a simple excel sheet to calculate a flared port, providing- effective surface area
- effective length
- enclosure tuning frequency
- suggested flare roundover radius
- effective exterior diameter, which can be defined using my method explained in post #595, based on strouhal number
- actual port length
- speed of sound
- and (net) enclosure volume
there are two warning fields that will turn yellow
- if the port length and the effective exterior diameter combination leads to intersection of flares (thus sealing the port)
- if the ratio between central minimum surface and exterior port surface is smaller than 1/10. this is just a safety feature based on my tests, where narrowing the central cross section area to 10% of port mouth area worked flawlessly. It might even be possible to extend this ratio
NFR (normalized flare rate) is fixed to 0,5 for this first version, thus the flare radius is equal to the actual port length.
you can use your defined actual port length and the calculated effective surface area to feed a simulation tool of your choice with data for a equivalent tube port. the tuning of this simulation will be correct, but the air speeds / air particle displacement and the volume occupied by port will not.
The excel sheet is protected except user data fields just to avoid unintended changes, but there is no password protection, so feel free to unlock it!
If you find any bugs please let me know!
Attachments
Awesome stv! Couple questions/comments...how are you handling end correction in the spreadsheet? I would prefer a user input, or, for less complexity, use no end correction and leave it to the user according their build methods. Also, you might verify the predicted Fb is correct by printing a variety of ports and measuring impedance. I've had a heck of a time predicting the length for my ports (which are Roozen-type and NFR=.5 also). I think it is mostly tied to aspect ratio of the port minimum diameter and length, but it is not a straight line relationship, but a curve. I have not had time to do more work on this, so I look forward to any results you might get to verify tuning.
Simple Excel sheet for calculating a flared port with NFR=0,5
I used basic geometry and the formulas by salvatti/devantier/button and set up a simple excel sheet to calculate a flared port, providing
For convenience the user data to be fed into the calculator is
- effective surface area
- effective length
- enclosure tuning frequency
- suggested flare roundover radius
The excel sheet also includes a sketch indicating the geometry.
- effective exterior diameter, which can be defined using my method explained in post #595, based on strouhal number
- actual port length
- speed of sound
- and (net) enclosure volume
there are two warning fields that will turn yellow
both warnings ask you to increase the effective exterior diameter or decrease the actual length.
- if the port length and the effective exterior diameter combination leads to intersection of flares (thus sealing the port)
- if the ratio between central minimum surface and exterior port surface is smaller than 1/10. this is just a safety feature based on my tests, where narrowing the central cross section area to 10% of port mouth area worked flawlessly. It might even be possible to extend this ratio
NFR (normalized flare rate) is fixed to 0,5 for this first version, thus the flare radius is equal to the actual port length.
you can use your defined actual port length and the calculated effective surface area to feed a simulation tool of your choice with data for a equivalent tube port. the tuning of this simulation will be correct, but the air speeds / air particle displacement and the volume occupied by port will not.
The excel sheet is protected except user data fields just to avoid unintended changes, but there is no password protection, so feel free to unlock it!
If you find any bugs please let me know!
View attachment 1317588
0.84hz tune in a 1ft3 enclosure with a 1" diameter x 1" length port?
yes, with a speed of sound of 10 m/s, as you defined.0.84hz tune in a 1ft3 enclosure with a 1" diameter x 1" length port?
you might just leave it at 340 m/s or change it according to your meteorological situation (but that won't change it to 10 m/s).
"In Earth's atmosphere, the speed of sound varies greatly from about 295 m/s (1,060 km/h; 660 mph) at high altitudes to about 355 m/s (1,280 km/h; 790 mph) at high temperatures."
https://en.wikipedia.org/wiki/Speed_of_sound
thanks for your suggestions, @augerpro!
that's what I suggested for using the data in a simulation program:
that seems to be quite OK, but I will do further verification measurements!
Would you mind checking the tool with some of your test ports?
I quickly realized one issue (or feature?) in my tool: it is a bit "dangerous" to calculate the most important parameter (the minimum diameter) based on the unprecise ("soft") effective exterior diameter parameter.
I should probably add a remark that for verifying an existing flared port it's essential to get the center diameter right, even if the exterior diameter differs slightly.
But I guess it is OK for defining the geometry for a port still to be built.
so did I - the third port in the above table was such a failed part for my other test speaker.
exactly! That's how the salvatti et al. formula works (post #600).
My excel sheet first calculates the minimum diamater geometrically, using the length and the exterior diameter, for convenience.
It follows the formula by salvatti/devantier/button and it's incredibly simple: you just add the minimum diameter to the actual port length. see post #600 with the relevant paper excerpt.how are you handling end correction in the spreadsheet?
That's again very simple: just use the the actual length input data and you have no end correction values added.I would prefer a user input, or, for less complexity, use no end correction and leave it to the user according their build methods.
that's what I suggested for using the data in a simulation program:
you can use your defined actual port length and the calculated effective surface area to feed a simulation tool of your choice with data for a equivalent tube port. the tuning of this simulation will be correct, but the air speeds / air particle displacement and the volume occupied by port will not.
I already did that, but here is a more refined and extended comparison table:Also, you might verify the predicted Fb is correct by printing a variety of ports and measuring impedance.
| BIG port 10 cm length 5,76 cm effective exterior diam. (3 cm minimum diameter) | MEDIUM port 9,4 cm length 5,55 cm effective ext. diam. (3 cm minimum diameter) | reused failed "progressive geometry" port from my bandpass test speaker 7,26 cm length 4 cm eff. ext. diam. (2 cm minimum diameter) | |
| measured tuning frequency (impedance phase = 0° between bass reflex peaks) | 48,9 Hz | 49,8 Hz | 39,0 Hz |
| tuning frequency as calculated with excel tool | 48,86 Hz (-0,08%) | 49,32 Hz (-0,96%) | 38,62 Hz (-0,97%) |
| tuning frequency using effective port surface area and the actual port length and simulating in hornresp | 50,4 Hz (+3,07%) | 50,9 Hz (+2,21%) | 39,8 Hz (+2,05%) |
that seems to be quite OK, but I will do further verification measurements!
Would you mind checking the tool with some of your test ports?
I quickly realized one issue (or feature?) in my tool: it is a bit "dangerous" to calculate the most important parameter (the minimum diameter) based on the unprecise ("soft") effective exterior diameter parameter.
I should probably add a remark that for verifying an existing flared port it's essential to get the center diameter right, even if the exterior diameter differs slightly.
But I guess it is OK for defining the geometry for a port still to be built.
I've had a heck of a time predicting the length for my ports (which are Roozen-type and NFR=.5 also).
so did I - the third port in the above table was such a failed part for my other test speaker.
I think it is mostly tied to aspect ratio of the port minimum diameter and length, but it is not a straight line relationship, but a curve.
exactly! That's how the salvatti et al. formula works (post #600).
My excel sheet first calculates the minimum diamater geometrically, using the length and the exterior diameter, for convenience.
Last edited:
- Home
- Loudspeakers
- Multi-Way
- Investigating port resonance absorbers and port geometries