This is important and thank you for reminding me- I shall cover this...
Although not totally on-topic, but it does make you wonder how much effect the FET-source-follower/common-drain mod would have an effect on these numbers?
Most capsules I have seen, are all connected as regular gain amplifier, introducing all kinds of issues.
That is just the active part inside the capsule itself. (not talking about the preamp after)
Not even the mechanical part.
Most capsules I have seen, are all connected as regular gain amplifier, introducing all kinds of issues.
That is just the active part inside the capsule itself. (not talking about the preamp after)
Not even the mechanical part.
The FET connection has a lot to do with distortion and signal handling in electret mics. They operate with essentially zero gate-to-source bias voltage, and as the junction forms a silicon diode, the gate starts to conduct when the voltage goes very much positive at all. At the usual diode multi-milliamp 'fully conducting' voltage of 0.6V, and a mic with typical sensitivity of 10mV/Pa, the level at the mic would be 129dBSPL. But as even tiny currents upset the electret operation, the mic has gone into extreme distortion (rectification) long before that. The common drain connection helps that a lot, a cascode helps even more.
Whilst fine tuning /calibrating the Brüel & Kjær measurement system, I thought I would share some measurements taken with the different processes with the software STEPS and REW.
These are taken with same drive level ~2.83V at speaker terminals, with a 44.1 KHz sample rate, of an un-marked 5.25” mid woofer in a ~1/4 cu ft enclosure, ported with a tuning frequency of 45Hz.
The microphone is 31.6cm from the baffle, on axis with the midwoofer. SPL id accurate to +/- 0.5 dB.
STEPS: 1/48 octave- time taken for test: ~12 mins
STEPS: 1/24 oct- time taken for test: 6 mins
REW Stepped sine, 24 points per octave.
default settings (64K FFT, Rectsngular window. 2 repeats) Time taken for test~18 mins
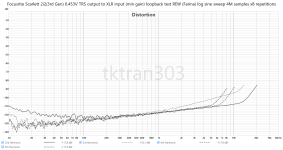
REW (Farina log sine) Sweep, settings 256K samples x8 repetitions: time taken: 45 seconds:
Some commentary is in order, I think, in order to aid interpretation of these graphs, for those unfamiliar with the software packages.
STEPS uses a stepped sine measurement process. The details of this process is beyond the scope of this post, however it is clear it provides the most detailed measurement. The disadvantage is the time taken to perform the test (minutes)
REW’s stepped sine function (accessible from RTA measurement Icon)it provides as much useful data as STEPS. So at least that’s consistent. But, is very slow. (If anyone can give me tips on how to speed it up- that would be much appreciated).
On the other hand, with REW’s standard Sweep function, by repeating the measuring 8 times to improve the signal to noise ratio (almost 10dB) over a standard single sweep measurement (not shown).
Furthermore, it smooths the fundamental with a 1/24th octave filter (fixed, non-deferrable) and shows harmonic curves that are much easier for our eyes/brain to interpret. Plus, it much faster.
Coming up- The Purifi midwoofer back under the attention of the Brüel & Kjær, as well as REW’s new FSAF (Fast subband adaptive filtering) measurement process (currently in beta testing) which measures harmonic and intermodulation distortion simultaneously, using noise signals or your choice of music clip/track
These are taken with same drive level ~2.83V at speaker terminals, with a 44.1 KHz sample rate, of an un-marked 5.25” mid woofer in a ~1/4 cu ft enclosure, ported with a tuning frequency of 45Hz.
The microphone is 31.6cm from the baffle, on axis with the midwoofer. SPL id accurate to +/- 0.5 dB.
STEPS: 1/48 octave- time taken for test: ~12 mins
STEPS: 1/24 oct- time taken for test: 6 mins
REW Stepped sine, 24 points per octave.
default settings (64K FFT, Rectsngular window. 2 repeats) Time taken for test~18 mins
REW (Farina log sine) Sweep, settings 256K samples x8 repetitions: time taken: 45 seconds:
Some commentary is in order, I think, in order to aid interpretation of these graphs, for those unfamiliar with the software packages.
STEPS uses a stepped sine measurement process. The details of this process is beyond the scope of this post, however it is clear it provides the most detailed measurement. The disadvantage is the time taken to perform the test (minutes)
REW’s stepped sine function (accessible from RTA measurement Icon)it provides as much useful data as STEPS. So at least that’s consistent. But, is very slow. (If anyone can give me tips on how to speed it up- that would be much appreciated).
On the other hand, with REW’s standard Sweep function, by repeating the measuring 8 times to improve the signal to noise ratio (almost 10dB) over a standard single sweep measurement (not shown).
Furthermore, it smooths the fundamental with a 1/24th octave filter (fixed, non-deferrable) and shows harmonic curves that are much easier for our eyes/brain to interpret. Plus, it much faster.
Coming up- The Purifi midwoofer back under the attention of the Brüel & Kjær, as well as REW’s new FSAF (Fast subband adaptive filtering) measurement process (currently in beta testing) which measures harmonic and intermodulation distortion simultaneously, using noise signals or your choice of music clip/track
Last edited:
I think if anything, it's extremely clear that all measurements are basically the same?
If not basically exactly the same for all practical purposes.
The REW log sweep (or rather exponentially swept sine as Farina named it) is surprisingly bad: the HF response is smoothed out and the noise floor high and rising.
The real quality metric is how far down the noise floor is when we have to resolve very weak higher harmonics. this is where the stepped sine is best because it accumulates the signal energy over long time.
The type of smoothing and window also determine the noise floor. For exponentially swept sines we have a pink signal spectrum which means that the noise per Hz goes up 3dB/octave. This can be flattened by using the correct smoothing in the complex domain or a window that shrinks with frequency when using an FFT.
I use custom chirps optimised in Matlab and complex smoothing. I get a noise floor down to around -20dB re 20uPa using a 200V mic at 40cm and normalised to 1m.
The real quality metric is how far down the noise floor is when we have to resolve very weak higher harmonics. this is where the stepped sine is best because it accumulates the signal energy over long time.
The type of smoothing and window also determine the noise floor. For exponentially swept sines we have a pink signal spectrum which means that the noise per Hz goes up 3dB/octave. This can be flattened by using the correct smoothing in the complex domain or a window that shrinks with frequency when using an FFT.
I use custom chirps optimised in Matlab and complex smoothing. I get a noise floor down to around -20dB re 20uPa using a 200V mic at 40cm and normalised to 1m.
Since you refer the measured noise to 20 uPa, then I understand that you are talking about the acoustic noise floor. I would like to know how you measured such a low noise level (which is, actually, very close to the fundamental acoustic noise level due to Brownian motion of the air molecules) ?
Last edited:
The noise floor is lowered by using a very long and slow chirp. It’s like using a very long FFT where each bin is a very narrow band filter that picks up less of the wide band noise from the mic path. The signal we analyse is deterministic (a pure sine wave ) whilst the noise is random. by averaging we improve the signal to noise ratio. A twice as long sweep lowers the noise by 3dB
That's great and all, but any form of noise averaging this way goes with a 10*log
So even with 64 averages (in any shape, form or duration), we will get a reduction of about 18dB
(in practice it's less optimistic)
So I am also still very curious how to measure that low?
The average background noise is somewhere around 25-40dB(A).
Reaching 10-20dB(A) of background noise is already incredible hard.
One airconditioning unit or a couple of other devices with a fan in your lab, and it's bye bye low background noise.
If we leave out the A-weighting, below (roughly) 50Hz there is a ton of low noise rumble that is often significantly higher.
Last edited:
I ran a quick test of the effect of averaging on the level of random noise coming from the input of the sound card. After more than 10,000 linear averages, the self noise dropped by approximately 40 dB (approximately that is how it should be theoretically). (dark yellow - no average, green - 10590 averages, light yellow - difference of the both curves). Looks like it's true
nice example!
The mic noise spec is for 0-20kHz, ie the noise power on that frequency range is say 20dB SPL. That means that if we observe the mic through a 20kHz low pass filter and sample at 40kHz then the output samples will have a statistical variance corresponding to 20dB SPL. If we then average more consecutive samples we get a simple FIR filter known as a sinc filter. The Bandwidth shrinks as the number of samples N increases, BW~1/N. For N=64k (1.5 sec) we get a variance (noise power) scaled down by 16•3=48dB. This is how a 64k FFT works: the apparent noise floor drops by 48dB
The mic noise spec is for 0-20kHz, ie the noise power on that frequency range is say 20dB SPL. That means that if we observe the mic through a 20kHz low pass filter and sample at 40kHz then the output samples will have a statistical variance corresponding to 20dB SPL. If we then average more consecutive samples we get a simple FIR filter known as a sinc filter. The Bandwidth shrinks as the number of samples N increases, BW~1/N. For N=64k (1.5 sec) we get a variance (noise power) scaled down by 16•3=48dB. This is how a 64k FFT works: the apparent noise floor drops by 48dB
yes very true. the background noise will typically dominate over the mic self noise.
the best case -20dB SPL is in the 5kHz. most background noise is dominated by low frequency energy and has a falling spectrum. We measure in a chamber that is sealed and with wedges which helps.
Stepped sine sweeps: extremely good for resolving harmonics. However, the frequency response is only sampled at discrete frequencies (steps) without prior smoothing (aka anti aliasing filtering). We could have frequency steps on either side of a very high Q resonance and completely missing it.
i wonder what Klippel NFS is doing. Anyone knows?
i wonder what Klippel NFS is doing. Anyone knows?
It’s a sweep.
The anechoic result from the NFS gets combined with an in-room non-anechoic result and the ISC module from Klippel to get anechoic data
Details:
https://www.klippel.de/fileadmin/kl..._System/PDF/S62_In_Situ_Room_Compensation.pdf
The microphone is a 1/2” pre-polarised capsule powered by IEPE constant current power supply,. It has 20Hz-20Khz and 15-135dB capability.
The anechoic result from the NFS gets combined with an in-room non-anechoic result and the ISC module from Klippel to get anechoic data
Details:
https://www.klippel.de/fileadmin/kl..._System/PDF/S62_In_Situ_Room_Compensation.pdf
The microphone is a 1/2” pre-polarised capsule powered by IEPE constant current power supply,. It has 20Hz-20Khz and 15-135dB capability.
Last edited:
I've read all of you all's posts, back and forth about noise.
All well and right.
But...
What really counts is the:
The "apparent noise floor" in:
is very very low !
best regards,
Bernd
All well and right.
But...
What really counts is the:
I searched for a long time for a suitable term, or words. That's it. Thank you 🙂
The "apparent noise floor" in:
REW (Farina log sine) Sweep, settings 256K samples x8 repetitions: time taken: 45 seconds:
is very very low !
best regards,
Bernd