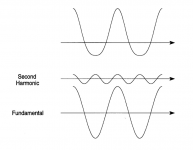
Think about where it can go when you start breaking down the waveform at the cycle level in a regular way.
Harmonic distortion of an audio amplifier can be as simple as the transfer function of the amplifier active device.
The active device can be a single vacuum tube, bipolar transistor, MOSFET, JFET, or other amplifying device.
When ever the input to output curve is anything other than a straight line graph, then whenever a pure single frequency tone is applied at the input, there will be one or more harmonic frequencie(s) at the output that are 2X, 3X, 4X, 5X, etc. times higher frequency than the original un-distorted tone.
The frequency response of the active device can be far below, and many times higher than the original tone, with no resonances present in the audio range; but the imperfect transfer function will produce that/those harmonic frequency(s).
This is an amplfier, not a loudspeaker.
Loudspeakers have resonances.
Most Good amplifiers do not have resonances in the 20HZ to 20kHz frequency range.
Hopefully that will make it clearer, and not distort the real principles of amplifer harmonic distortion.
Loudspeakers not only have resonances, they also have a transfer function, output versus input.
If the transfer function is not a straight line, input versus output, then for a single pure tone in, there will be one or more of these harmonic frequency(s), 2X, 3X . . . etc.
Now, when 2 tones are applied to an amplifier
and/or when 2 tones (within the bandwidth of a driver and its crossover) are applied to a speaker . . .
. . . there will be Intermodulation distortion tones in addition to the original 2 tones, but that is a subject for another thread.
The active device can be a single vacuum tube, bipolar transistor, MOSFET, JFET, or other amplifying device.
When ever the input to output curve is anything other than a straight line graph, then whenever a pure single frequency tone is applied at the input, there will be one or more harmonic frequencie(s) at the output that are 2X, 3X, 4X, 5X, etc. times higher frequency than the original un-distorted tone.
The frequency response of the active device can be far below, and many times higher than the original tone, with no resonances present in the audio range; but the imperfect transfer function will produce that/those harmonic frequency(s).
This is an amplfier, not a loudspeaker.
Loudspeakers have resonances.
Most Good amplifiers do not have resonances in the 20HZ to 20kHz frequency range.
Hopefully that will make it clearer, and not distort the real principles of amplifer harmonic distortion.
Loudspeakers not only have resonances, they also have a transfer function, output versus input.
If the transfer function is not a straight line, input versus output, then for a single pure tone in, there will be one or more of these harmonic frequency(s), 2X, 3X . . . etc.
Now, when 2 tones are applied to an amplifier
and/or when 2 tones (within the bandwidth of a driver and its crossover) are applied to a speaker . . .
. . . there will be Intermodulation distortion tones in addition to the original 2 tones, but that is a subject for another thread.
No, it´s not, at all, not sure what´s your ´point for saying so.
Are you trying to stir the pot for some unknown reason?
Resonances happen at certain defined frequencies.
Suppose we have a pipe, fundamental resonance is , say, 1 kHz, then it will have higher resonant modes or resonances.
Which will be multiples of the fundamental, so 2000/3000/4000/5000Hz and so on.
So far, superficially the same as what we see in the graph.
But the BIG difference is that those resonances, to be so, must stay there.at those frequencies, once determined they can not take other unrelated values.
So if instead we inject 1200 Hz, you will NOT have resonances t 2400/3600/etc. Hz, they will still be at 2k/3k/4kHz,etc.
Re-so-nan-ces .... ring a bell?
While a distorted signal will have exact multiples of fundamental, no matter what the fundamental is, an essential difference.
You inject 1100HZ?
Sure, now will find 2200/3300/4400/etc. Hz.
Completely different.
A phenomenon NOT explained by resonances, and fully explained by Harmonic Distortion.
Actually, you are wrong.
The harmonic distortion is BY DEFINITION whole, integral multiples of the fundamental input frequency.
Hence, if the input is 1Khz, the harmonics will be at 2, 3, 4, 5....
If the input is at 1.2Khz, the harmonics will be at 2.4, 3.6, 4.8, 6... etc...
A resonance is a harmonic of the fundamental. Interesting... think of the close and open pipe air resonances.
So, assuming that the non linearity of a circuit introduces higher order distortion....
..WHY would it be that it is in whole integral harmonics?
Why does a 1Khz signal generate harmonics at 2, 3, 4 etc?
I find he concept of harmonics interesting. Specifically how does a system magically settle into a harmonic.
Electrically this disappears down the Quantum rabbit hole - with the energy of the wave function only appearing as a whole wave multiple. My layman’s understanding. All caused by the wave aytempting to get to the lowest energy representation thus a square wave brakes into infinite lowest energy waves possible. Those are observed as harmonics.
I assume the same is present for speakers. The complication is the number of materials that all have their own harmonic breakdown - be it capacitors, circuit copper or plyswood, speaker materials or air.
However in that scenario I assume THD is simply how much energy you’ve lost from the original wave following the breakdown mentioned above.
I’m not a physicist or EE, just happened to have worked in a quantum research company where the majority of employees were PHD degree+ level including ex-oxford /ex-cambridge professors. That’s my unqualified laymans understanding.
Nobody could give me a laymans answer to why multiples other than the wave form is bounded… physically/mathematically why should that be?
We have maths describing observations made to explain the behaviour. I’ve not seen a good layman’s explaination of wave functions to say why we actually get multiples other than point to the maths.. which describes out best guess of the behaviour.. and doesn’t answer the underlying why…
Last edited:
It does not assume, but fact.
You should learn Fourier analysis about waveform.
https://www.techtarget.com/whatis/d...lysis is a method,the 18th and 19th centuries.
I doubt you are learn Physics.
I think I can almost answer my, and your, question:
Why do we see whole integer multiples (harmonics, resonances) of the fundamental signal?
It's almost an empirical proof of the Fourier Theorem about waves: where a wave can be defined by a series of harmonics.
I believe this is because we are measuring it in a frequency domain.
Perhaps a much better distortion measurement would be to do it in an analog, amplitude domain: we could measure the output wave of the electronic circuit's transfer function, then subtract the input signal and see the distortion. It will be harmonic, of course. It will "beat" with the input signal because it is the distortion of the input signal, which itself is repetitive.
If we wanted to, we could then also put that difference distortion signal though a frequency domain analysis and see the harmonic spectrum.
I’m aware of the fourier maths describing the observed behaviour - however i assume the driver is the energy breakdown (entropy) on finding the smallest possible waveform is plank’s constant, which results in a having to fit into a multiple of planks waveform the ripple effect at a macro level is we get the breakdown of energy into a fundamental and harmonics. That resulting behaviour is what is described by Fourier maths.
Which also works in reverse, harmonics can be shown to restore the non-linearity..
Because the non-linear transfer function is constant.
Jesus Christ.... the **** vinegar is deep in this forum...
In Western Empitical Science we always ASK questions... What YOU take as a fact, I see as a particular observation based on some coincidence.
The thing is that "non linearity" is a loaded term. What kind of "non linearity" are we discussing? A gain transfer function issue?
Where V = F(v) is not a linear function, F' is not constant, and V != F(v, t) ....where 't' introduces the frequency component?
They hired the wrong person who did not know about Fourier analysis. If you did not know about transfer function of amplifier, I understand because you are not EE as you said. You can also learn about Laplace function.
Resonance is a phenomenon generally associated with linear differential equations. It can occur in nonlinear systems too, but the point is that it is a feature of linear systems ... that don't have any harmonic distortion by virtue of being linear
Harmonic distortion only exists in nonlinear systems, and doesn't necessarily have anything to do with differential equations
The Dunning-Kruger effect runs strong in this thread
Harmonic distortion only exists in nonlinear systems, and doesn't necessarily have anything to do with differential equations
The Dunning-Kruger effect runs strong in this thread
Earlier I talked about the non-linearity being constant, as you'd consider with regard to amps, speakers and many things. If you try reconstructing using non harmonically related signals, the linearity (would have to) varies.
I'm almost sure that TonyEE meant "transfer characteristic" but somehow ended up writing "transfer function" instead. And, neither EEs nor profs are very good at providing "layman definitions" for technical terms, as that's not what they're used to. Most try their best to help, but you can't blame them for not being able to meet others' expectations.
Ahh - excellent question! If you take a sine wave, and run it through a non-linear process, the waveshape is distorted. The tops can be squashed or increased, or the symmetry around the zero crossings becomes different between rising and falling edges.
Enter Mr. Jean-Baptiste Joseph Fourier, French mathematician. He found out that if you start from a perfect sine wave you can 'build' any distorted sine wave by adding harmonics of the signal in specific levels and phase shifts! Turning that around, you can take any distorted sine wave and unravel it into the fundamental perfect wave and a collection of equally perfect waves at harmonic frequencies in specific levels and phases.
This is done by mathematical manipulation of the signal wave. FFT comes to mind, of course.
I always find these things extremely interesting. I mean, how do the mathematics 'know' how the physical systems work? (No answer required ;-).
Edit: you can also unravel the signal into the fundamental and harmonics in a series of filter banks, set to each of the frequencies. But that's sooo 20-th century ;-)
There is also a philosophical question here. Does the amp create the harmonics, or does the FFT?
Suppose we find another mathematical process to unravel a distorted signal but it gives the fundamental and 1.5x harmonics, and it can perfectly re-assemble the distorted wave from those components. Do we then say that the amp creates 1.5 multiple 'harmonics'?
Jan
Last edited:
It sort of works backwards.
Mathematicians work on relationships, pure relationships.
Then physicists build models and they find mathematical constructs that are useful.
Mathematicians really don't know, they actually don't care, about physical models at all.
It's like this... I recall the one day in class when we were looking at gravity and the professor asked: "What happens if we take this to the limit".. and lo and behold the mathematics used in the model pointed out something interesting... the event horizon of a black hole!
Before that, I always wondered about the same thing you were asking... "how do mathematicians know?"... but then it become obvious that they really don't know. That was the day, as a junior in college, when I became a physicist... I figured out how to think like a physicist.
It's like the guy who builds a hammer and a saw, he's not an architect, but without those tools the architect would not even start to design a house because he would not know how to express a design that could be built. The architect may not know, or care, how to design a hammer, but he can design stuff that can be built with a hammer.
It is very interesting indeed.
Another example would be calculus. Newton was working on limits, not very elegant but along came Leibnitz and he created calculus based upon his philosophical question of time change. How to express change... is time continuous or a bunch of discrete events? Now, Newton would have used limits ( he did, to calculate energy ) but Leibnitz was after a far deeper thought... change.
Eventually, physicists, natural philosophers then, figured out the usefulness of Leibnitz's work.
As an aside, if you like intelligent science fiction, read Neil Stepheson's The Baroque Cycle, it is an awesome read and it involves Newton, Leibnitz, Physics, The Dark Plague, etc...
Last edited: