I believe the spectrum and levels of HOMs currently cannot be mathematically derived due to the complexity. Just like the fact the same of baffle edge diffraction (not the baffle step response) because it is so driver and edge dependent in reality.
Lynn Olson said:
It would likely be very spiky, not flat or smooth at all. The modes have sharp high-Q cut-ins which increase in amplitude as the mode number goes up. So the response would be anything but smooth. At a high enough mode number it would be virtually a very sharp high-Q resonance - much like the LF modes in a totally undamped room. Yes, higher and sharper Q as the frequency goes up, more dense too. In a 1" driver there are maybe 5-8 modes in the audible band. For a 2" this would likely quadruple.
Sorry for pestering you about the HOM's - but I'm curious, and without question you are the most knowledgeable person to ask. Are these modes (highly) directional, or do they emerge from the entire mouth of the horn or waveguide and diverge smoothly outward?
Or does each mode point in a different direction, depending on the internal source of diffraction within the horn or waveguide (similar to the complex 2D patterns that appeared across the mouths of the test horns on pages 60 through 66 of the Morgans thesis)?
Or does each mode point in a different direction, depending on the internal source of diffraction within the horn or waveguide (similar to the complex 2D patterns that appeared across the mouths of the test horns on pages 60 through 66 of the Morgans thesis)?
Attachments
The Morgans thesis seems to show large throats have difficulty diffracting the higher frequency waves, this is pretty much what I thought before browsing through it. Will the equation that Dr. Geddes provided be the optimum curve? This would be interesting to find out. The only thing is that the equation did not address the fact that be final beam width is still frequency dependent and thoat size dependent.
Lynn Olson said:
The answer is more like the later. Each mode will have a different directivity from every other one AND this will change with frequency. Clearly a situation that would be difficult to analyze. Thats why I simply take the posotion that I need to minimize these undesirable attributes and not worry too much about the details of how they propagate. If there aren't any, or they have been reduced as low as possible, then how they propagate is academic. So I really haven't studied the directivity of them very much. Gotfried Bueler did some work in this a few years back at AES. He showed that they were indeed complex in the patterns that they radiated. His work was purely experimental.
soongsc said:
Soonsc
You state so many things with authority that are simply not correct that it can make your posts is unsettling.
"The only thing is that the equation did not address the fact that be final beam width is still frequency dependent and thoat size dependent. "
This is incorrect and hence your use of the word "fact" is disconcerting.
And I have stated many times that I can prove that the OS curve is optimal.
I am referring to the equation in post #5. Whether the throat size and highest frequency of directivity control is addressed anywhere else, I am still looking. I am sure that if one used the equation in post#5 to contruct the wave guide with a 2" throat, it will not maintain good directivity control for beam width of 60 deg. This is also shown in the Morgans thesis.
I'm quite sure your design is optimum, I'm just thinking along the lines how to reduce HOMs without putting foam in the path, and also hope to reduce distance between the drivers, have a different vertical directivity pattern.
I'm quite sure your design is optimum, I'm just thinking along the lines how to reduce HOMs without putting foam in the path, and also hope to reduce distance between the drivers, have a different vertical directivity pattern.
Note that I probably never say whether anyone is wrong or not. Whether what I address is right or wrong, readers are free to make their own decisions as they wish. I probably never say I am right either. If anyone corrects me in a way I understand why I was wrong at any time, I will openly admit my mistakes. If I do not admit such, maybe I didn't have the same level of understanding.
My personal way of learning things is understanding of the functionality and phenomena first, if I do have a good feel for what is going on, then I will try to understand the math behind all this when necessary even though math is probably one of my weakest points.
My personal way of learning things is understanding of the functionality and phenomena first, if I do have a good feel for what is going on, then I will try to understand the math behind all this when necessary even though math is probably one of my weakest points.
modal suppresion
In microwave waveguides, transmission modes are suppressed and beam patterns adjusted in feedhorns using a variety of schemes, including corrugated scalar horns and other conformational variations.
http://www.quinstar.com/qsh_qsw_narrow_and_wide_beam_scalar_feed_horn.html
http://www.suparco.gov.pk/pages/antenna07.asp
While I realize that acoustics and microwave transmission are 2 completely disaparate fields, and the wavelengths are not necessarily comparable, I'm wondering (perhaps naively) if some form of surface modulation (beyond the OS waveguide smooth contour) might serve to further enhance suppression of HOM propagation, and or enhance the DI of the guides?
John L.
In microwave waveguides, transmission modes are suppressed and beam patterns adjusted in feedhorns using a variety of schemes, including corrugated scalar horns and other conformational variations.
http://www.quinstar.com/qsh_qsw_narrow_and_wide_beam_scalar_feed_horn.html
http://www.suparco.gov.pk/pages/antenna07.asp
While I realize that acoustics and microwave transmission are 2 completely disaparate fields, and the wavelengths are not necessarily comparable, I'm wondering (perhaps naively) if some form of surface modulation (beyond the OS waveguide smooth contour) might serve to further enhance suppression of HOM propagation, and or enhance the DI of the guides?
John L.
The answer would be yes, but of limited value. The effect would be small since the depth of any surface treatment would be small compared to a wavelength at anything but the very highest frequencies. But in effect, the way in which the foam plug is mounted will do exactly what you suggest, albeit more in a random form than a controlled on. The glue at the boundaries will create a rough surface which will tend to scatter the HOM as they inping upon it.
gedlee said:
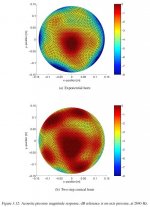
Your informative reply is very much appreciated - I had a feeling that if the frequency of the Morgans' plot was swept, the GIF would have to be animated, and the hotspots would move around quite a bit. What's a little weird is the five-pointed star pattern also appears faintly in the exponential test horn as well, which raises questions about slightly asymmetric mounting of the compression driver.
HOM's are clearly undesirable due to their severe narrowband effects in the frequency domain, spikes in the polar plots, and high-Q stored energy in the time domain - all of the things that have traditionally been "smoothed out" in the data from the prosound manufacturers. It's the fine-grained data that shows just how serious the problem really is, and has been for as long as traditional horns have been around. I wonder how different the Morgans paper would have been if they had chosen a HOM-minimization search algorithm instead of conformity to an idealized polar pattern.
I'd like to offer a sincere thanks for all of the extensive information you've posted in this thread, other threads, and your superb book. I hope the industry professionals who are reading this thread take note.
Lynne
Thanks.
It was the non-axi-symmetric results that were the most interesting to me. When I did the HOM solutions for the OS waveguide, I assumed axisymmetry and always wondered about this. The reason is that the non-axi-symmetry modes occur at frequencies well below the axisymmetric ones, so they are a more seriuos problem. Theoretically they should not exist in a purely axi-symmetric system, but Morgan shows very clearly that they do exist. How this happens is most curiuos indeed.
Its a real mystery, but one that I had a lot of evidence to suspect would be present. I first realized this after a conversation with Don Keele. He was tell me that when they rotated the driver on a waveguide they got a different polar pattern! Thats when I came to realize that real devices were anything but ideal.
It would be of great interest to me to study where these asymmetries come from. Alas, nobody does advanced work like this anymore.
Thanks.
It was the non-axi-symmetric results that were the most interesting to me. When I did the HOM solutions for the OS waveguide, I assumed axisymmetry and always wondered about this. The reason is that the non-axi-symmetry modes occur at frequencies well below the axisymmetric ones, so they are a more seriuos problem. Theoretically they should not exist in a purely axi-symmetric system, but Morgan shows very clearly that they do exist. How this happens is most curiuos indeed.
Its a real mystery, but one that I had a lot of evidence to suspect would be present. I first realized this after a conversation with Don Keele. He was tell me that when they rotated the driver on a waveguide they got a different polar pattern! Thats when I came to realize that real devices were anything but ideal.
It would be of great interest to me to study where these asymmetries come from. Alas, nobody does advanced work like this anymore.
Sure there is "enough energy in a sound wave to compress water", at least a very tiny amount (relative to air). Say, one part in a million, billion, trillion? Good to go. Ok? But a primary reason sound travels so fast in water is that it is relatively so incompressible.
Consider a spherical sound source immersed in water. In the real world, there is no way for it to propagate *without* compressing the water that surrounds it as it expands. Also, if the water didn't compress at all, the speed of sound in water would be infinite.
Think about it.
Only a single curve for all HOM modes of significance? Or is there room for adjustment for improved performance subjectively weighted?
The computational sequence of FEAs effects the results. Ideal conditions would tell us that there are no non-axisymentric modes. But due to computational sequence, they may occur, and one has to decide how realistic these should be considered.
IF the existance of HOMs are subjectively important, as they are, then simply reducing them is the best benefit. No shape for a circular source can be better that the OS curve. It is a catenoid of the second derivative and the second derivative is what generates the HOM. Hence The OS will generate the fewest.
Now your hypothesis would be that not all HOMs are EQUALLY bad and some curve other could have lower bad ones. A nice hypothesis, but without something to back it up I'll stick to what I am doing.
Now your hypothesis would be that not all HOMs are EQUALLY bad and some curve other could have lower bad ones. A nice hypothesis, but without something to back it up I'll stick to what I am doing.
Allow me a stupid question, but I dont understand this HOM when no one seems to have done any measurements to show its behaviour
How can you know the OS is superiour regarding HOM, is it by mathematical proove
Still, the OS also needs a foamplug
To me it sounds more like a matter of precise design of throath and curved mouth, which should be of benefit to any waveguide, and as I recall you have said so yourself
Its not dissbelief in any way and I dont mean to sound harsh ... only curious
How can you know the OS is superiour regarding HOM, is it by mathematical proove
Still, the OS also needs a foamplug
To me it sounds more like a matter of precise design of throath and curved mouth, which should be of benefit to any waveguide, and as I recall you have said so yourself
Its not dissbelief in any way and I dont mean to sound harsh ... only curious
Speaking for myself, the HOMs most suppression worthy (for a particular flare) would seem to be the ones that are both a) most audible (Fletcher-Munson & masking) and b) most likely to be strongly excited due to the spectral content of the expected program material to be reproduced, everything else being equal.
