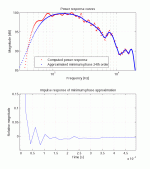
Is there any other way of power response estimation than average in freq. domain? The drawback of average is that phase information is lost. I did an experiment with Matlab to get minimum phase response of such a "power average" curve and presenting the results. I'm not sure if this makes any sense since horns aren't minimum phase devices (as far as I know).
The question rises equalising filter domain. Stay in frequency domain with multiplication or go to time domain with some minimum phase approximation?
The question rises equalising filter domain. Stay in frequency domain with multiplication or go to time domain with some minimum phase approximation?
Attachments
It could be done in the time domain but there would be no point in that.
In obtaining the power response from a set of polar curves you must remember that each curve does not represent the same area and the calculation must take this into account. This also points out the inadequacy of the axial response since it represents the smallest area of all of the curves and hence is vastly over respresented in a polar response plot.
In obtaining the power response from a set of polar curves you must remember that each curve does not represent the same area and the calculation must take this into account. This also points out the inadequacy of the axial response since it represents the smallest area of all of the curves and hence is vastly over respresented in a polar response plot.
This means that every curve must be normalised for constant area?
Power averaging removes horn reflections so convolution in time can make some sense?
Consider the manner in which we measure a driver - axial, 10°, 20°, etc. The axial measurement of pressure repersent a disk out to the 5° angle, the 10° measure an annulus from 5° to 15°, etc. you see the pattern? The power is proportional to the pressure squared times the area that it represents. These areas get greater as the angle increases meaning that the off-axis polar data has a greater effect on the power response than the axial does.
We could alternatly use Fresnel Zone areas such that each polar line represented the same area, but then this would give us far higher resolution off-axis than on axis.
I have often considered weighting the area in a polar map by the area the data represents which would then give a correct representation of the power response from polar pressure data, at least visually.
"Power averaging removes horn reflections so convolution in time can make some sense?"
I have no idea what you mean here.
We could alternatly use Fresnel Zone areas such that each polar line represented the same area, but then this would give us far higher resolution off-axis than on axis.
I have often considered weighting the area in a polar map by the area the data represents which would then give a correct representation of the power response from polar pressure data, at least visually.
"Power averaging removes horn reflections so convolution in time can make some sense?"
I have no idea what you mean here.
"The axial measurement of pressure repersent a disk out to the 5° angle, the 10° measure an annulus from 5° to 15°, etc. "
So the contribution of the on-axis response is zero; I can see why you think it's overrated.
So the contribution of the on-axis response is zero; I can see why you think it's overrated.
Well I thought horn is non-minphase device because of higher modal wave propagation (internal reflections, diffractions) in contrast to direct radiators. With pressure averaging we lower the magnitude of reflections in total transfer function thus then the response is more minimum phase.
noah katz said:
I don't follow. Its small, but its not zero. A disk out to 5° is still of finite size (its r^2 sin(5°) where r is the measurement distance, the next point is r^2(sin(15°)-sin(5°)), - nearly twice as big - etc.)
I almost put a smiley in, but I'm on the level - a cone with 0° included angle sweeps out zero volume/area.
But that's not the issue. The central point represents the sampled pressure on a disk that subtends a solid angle of 2 x 5°, which is not zero. The next point represents the axisymetric (assumed) sampled pressure on an annulus that goes from 5° to 15°, and so on. Your "point" is incorrect - thats why I thought you were joking.
Ah, I wasn't aware of the convention for scalling out the curves on a polar response set.
Nevertheless, and albeit of no practical significance, I maintain that the power contribution of the on-axis response is zero.
Nevertheless, and albeit of no practical significance, I maintain that the power contribution of the on-axis response is zero.
You don't give up do you!!
Pressure is a force per area measurement and has no meaning if there isn't an area which it represents - it can't be zero!!
Pressure is a force per area measurement and has no meaning if there isn't an area which it represents - it can't be zero!!
"Pressure is a force per area measurement and has no meaning if there isn't an area which it represents - it can't be zero!!"
Zero has as much meaning as any other number, although of no utility here.
Remember, the point I was making was academic.
Zero has as much meaning as any other number, although of no utility here.
Remember, the point I was making was academic.
"A cone with 0° included angle sweeps out zero volume, and the area of the endcap is zero."
What's incorrect about this statement?
What's incorrect about this statement?
The smell of bandwidth burning...
C'mon guys... Yer killing me here.
I'm subscribed, so I'm getting an email with every nuh-uh/uh-huh...
C'mon guys... Yer killing me here.
I'm subscribed, so I'm getting an email with every nuh-uh/uh-huh...