Hi Jorge,
actually I for one appreciated the posting. And of course phase and group *delay* relate to each other in the standard formulas.
Unfortunately this kind of subject always goes into mud slinging. Incidentally I start getting an allergy to the type of "the formulas clearly explain" postings. The formulas don't explain anything. They formalize some basic assumptions, build on them, and allow prediction of behaviors. As such they are just models. I find it more refreshing to see things from different angles, especially when they don't contradict the sacred formulas. If something contradicts the sacred formulas, naturally, the author has a lot of explaining to do. But in these forums it seems like sacrilege merely to restate the Universal Truth represented by The Formula in a different way... such as referring to first priciples which is where The Formula came from to begin with.
Anyway just a rant. I come here to learn and for entertainment but often I just get summary answers such as "The Holy Formula has explained all this and more and if you weren't such a dunce you'd know".
It seems there are 3 kinds of people here:
- the ones not well seated enough in the engineering specifics to make themselves clear - me as an example
- the ones who know the engineering and its ambiguities and assumptions very well, such as the great names. They usually don't participate at length precisely because of the ambiguities and hidden assumptions - it's a minefield of contention
- the ones that learned the formulas, apply them every day, and never think about the first principles or how they came about. They're so happy they finally understood The Formula and found The Truth that they react very angrily at anybody taking a different view - even a view consistent with The Formula, just expressed from a different angle.
Eva:
you say that radically different waveforms such as the ones you presented will always sound the same. In other words, you seem to say that wave form, hence delay, hence time, plays no role in audio sensory perception - that only time independent frequency content matters? I can't believe you really believe that.
actually I for one appreciated the posting. And of course phase and group *delay* relate to each other in the standard formulas.
Unfortunately this kind of subject always goes into mud slinging. Incidentally I start getting an allergy to the type of "the formulas clearly explain" postings. The formulas don't explain anything. They formalize some basic assumptions, build on them, and allow prediction of behaviors. As such they are just models. I find it more refreshing to see things from different angles, especially when they don't contradict the sacred formulas. If something contradicts the sacred formulas, naturally, the author has a lot of explaining to do. But in these forums it seems like sacrilege merely to restate the Universal Truth represented by The Formula in a different way... such as referring to first priciples which is where The Formula came from to begin with.
Anyway just a rant. I come here to learn and for entertainment but often I just get summary answers such as "The Holy Formula has explained all this and more and if you weren't such a dunce you'd know".
It seems there are 3 kinds of people here:
- the ones not well seated enough in the engineering specifics to make themselves clear - me as an example
- the ones who know the engineering and its ambiguities and assumptions very well, such as the great names. They usually don't participate at length precisely because of the ambiguities and hidden assumptions - it's a minefield of contention
- the ones that learned the formulas, apply them every day, and never think about the first principles or how they came about. They're so happy they finally understood The Formula and found The Truth that they react very angrily at anybody taking a different view - even a view consistent with The Formula, just expressed from a different angle.
Eva:
you say that radically different waveforms such as the ones you presented will always sound the same. In other words, you seem to say that wave form, hence delay, hence time, plays no role in audio sensory perception - that only time independent frequency content matters? I can't believe you really believe that.
Because if a waveform of that frequency is suddenly added to the input, the output will instantaneously react in such a way that it will start progressively showing the input waveform 90 degrees out of phase (note that this is a complex process since infinite frequencies may be used in the instant a new component is added to a signal).
On the other hand, in a system with 250uS of delay, the output will take 250uS to react against any change in the input.
MBK said:
I think this was demonstrated back in 1970s, we can't hear phase differences between different frequencies, we can only hear phase differences between each ear at the same frequency. I have actually built several phase shifters for active crossover prototypes so I've had the chance to check it. Both waveforms sound exactly the same, believe me or dare to do the experiment. Also, you are again mistaking phase and delay.
Eva,
ok your example was not about delay but about effects of phase shift. Then again we could argue that phase shift is a transformation of delay modulo 2Pi... or am I wrong ?
BTW I can believe that certain things in the wave form are not audible, the ear seems most sensitive to zero crossing and that only in one direction...
But fundamentally, and please explain it away in detail if you must, things such as phase are shifted by processes involving *time*, such as the charging time given by dC/dT in a capacitor.
ok your example was not about delay but about effects of phase shift. Then again we could argue that phase shift is a transformation of delay modulo 2Pi... or am I wrong ?
BTW I can believe that certain things in the wave form are not audible, the ear seems most sensitive to zero crossing and that only in one direction...
But fundamentally, and please explain it away in detail if you must, things such as phase are shifted by processes involving *time*, such as the charging time given by dC/dT in a capacitor.
Eva said:
Eva,
this is not explained exactly. In time domain, the RC circuit's step response is:
Vo = Vi(1 - exp(-t/RC)),
where Vo = output voltage, Vi = input voltage (step), RC = Tau = time constant.
In case of linearly rising input voltage Vi with constant slope, Vo, after initial transition of exponential shape, starts to follow Vi, but delayed by Tau. That means, Vo equals Vi after time Tau, which we consider as time delay of the RC circuit.
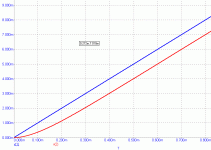
Just to clarify, I am attaching the response of the RC circuit, R = 1 Ohm, C = 100 uF (Tau = 0.1 s) to linear constant slope signal. The time delay of 0.1s (Tau) can be seen.
Attachments
PMA,
thanks for plugging in the formula... it seems one has to formalize it to be taken seriously 😉
thanks for plugging in the formula... it seems one has to formalize it to be taken seriously 😉
PMA your picture is rather self explaining: The output of any RC circuit reacts inmediately to input changes but with non-constant time-dependent amplitude, as opposed to what happens when a signal is delayed, where any change in the input appears at the output after some time. Since any input change is not delayed in RC circuits, the output is just reflecting the instantaneous value of the input signal with time-dependent attenuation.
The 'time constant' concept is just used to predict this time-dependent amplitude change.
By using your criteria we could even talk of time constants (and thus delays) in voltage dividers since the output signal takes some time to reach the amplitude the input signal had.
Also, try to find time constants for the phase-shifted square wave shown in one of my previous posts, then again, it was generated witn four RC cells...
If we call 'apples' to oranges, then, how are we supposed to call apples?
Red trace is the original signal. Blue trace is the same signal after passing through a RC filter, notice how it follows the input signal instantaneously altough its amplitude is altered. Green trace is a delayed copy of the input signal.
The 'time constant' concept is just used to predict this time-dependent amplitude change.
By using your criteria we could even talk of time constants (and thus delays) in voltage dividers since the output signal takes some time to reach the amplitude the input signal had.
Also, try to find time constants for the phase-shifted square wave shown in one of my previous posts, then again, it was generated witn four RC cells...
If we call 'apples' to oranges, then, how are we supposed to call apples?
An externally hosted image should be here but it was not working when we last tested it.
Red trace is the original signal. Blue trace is the same signal after passing through a RC filter, notice how it follows the input signal instantaneously altough its amplitude is altered. Green trace is a delayed copy of the input signal.
To further support & clarify Eva's above post, consider the fact that the voltage on a cap lags 90 degrees to the current charging the cap. However, there is NO time delay. At the very moment the current starts, the voltage starts also rise. But, if the current is a sinewave, the cap voltage, also a sine wave, will reach its maximum when the current is already past its maximum and is in fact going through zero again. That is the 90 degrees lagging phase shift. But it is not as if the current starts, nothing happens, and all of a sudden the voltage appears. The voltage rise (or decrease, depending on current polarity), starts from the exact moment the current starts.
This phase shift and its resulting difference between input signal and output signal against time is a form of linear distortion as discussed in another thread.
Jan Didden
This phase shift and its resulting difference between input signal and output signal against time is a form of linear distortion as discussed in another thread.
Jan Didden
OK, so we have again a problem of terminology. For Eva, only constant-time (group) delay can be called 'delay', any other time-dependent amplitude changes don't qualify for the term.
I actually thought a typical amplifier exhibits both some form of group delay, and these non-constant time dependent amplitude changes, usually AKA phase shift if they can be formalized as such.
How about this statement then:
Amplifiers exhibit both constant-time and non-constant-time dependent amplitude transfer functions. The output voltage of any instant input voltage in any case is thus subject to
Vout(t)=a*Vin(t-tconstant-tvariable)
It still appears to me that (tconstant+tvariable) > 0 , a positive time added to t, in common language a variable "delay".
In a periodic system you can get rid of the time term mathematically for the phase shift, because you will express the non constant time variable output as phase angle. Then time "disappears" in the equation, but it does not become "zero" (instant).
By the same token, say, frequency domain data give no information as to the waveform/at which time which frequency occurred. This does not mean the time at which it occurred was "instant". I'm not even sure whether the term "frequency" makes any sense for a nonperiodic instant dt. "Frequency", phase, etc, just only make sense under the assumption of periodicity. Apparently, theory predicts that you can extract at least some frerquency information out of a nonperiodic signal - it just doesn't make intuitive sense to me. That's why they are usually called "transients", not "tones" anyway.
Or do I make myself unclear again?
Your graph, Eva, btw shows the blue trace clearly appears *after* the red trace. It follows it shifted to the right, not "instantaneously" (in which case it would be superimposed).
I actually thought a typical amplifier exhibits both some form of group delay, and these non-constant time dependent amplitude changes, usually AKA phase shift if they can be formalized as such.
How about this statement then:
Amplifiers exhibit both constant-time and non-constant-time dependent amplitude transfer functions. The output voltage of any instant input voltage in any case is thus subject to
Vout(t)=a*Vin(t-tconstant-tvariable)
It still appears to me that (tconstant+tvariable) > 0 , a positive time added to t, in common language a variable "delay".
In a periodic system you can get rid of the time term mathematically for the phase shift, because you will express the non constant time variable output as phase angle. Then time "disappears" in the equation, but it does not become "zero" (instant).
By the same token, say, frequency domain data give no information as to the waveform/at which time which frequency occurred. This does not mean the time at which it occurred was "instant". I'm not even sure whether the term "frequency" makes any sense for a nonperiodic instant dt. "Frequency", phase, etc, just only make sense under the assumption of periodicity. Apparently, theory predicts that you can extract at least some frerquency information out of a nonperiodic signal - it just doesn't make intuitive sense to me. That's why they are usually called "transients", not "tones" anyway.
Or do I make myself unclear again?
Your graph, Eva, btw shows the blue trace clearly appears *after* the red trace. It follows it shifted to the right, not "instantaneously" (in which case it would be superimposed).
FORR
"The time resolution of the ear is at best, about 10 mS.
[...]
Audio signals have a finite rise time (my data indicate
that the fastest audio signal coming from a microphone
is about 10 mS)"
Ooops ! sorry, MIKEB, I mean : 10 µS, in both cases.
LUMANAUW
"If an amp having signal passing more of this B junction, you will get more
delay, because these capacitance have to be charged/discharged."
This is a demonstration of how to make myths grow in audio.
(note : not every body agrees that the cited amplifiers are audibly the best).
EVA
"The output of any RC circuit reacts inmediately to input changes but with
non-constant time-dependent amplitude, as opposed to what happens when a signal
is delayed, where any change in the input appears at the output after some time.
Since any input change is not delayed in RC circuits, the output is just
reflecting the instantaneous value of the input signal with time-dependent
attenuation."
This is the most understandable explanation of the whole story.
Curiously, there was an idnetical discussion a few weeks ago on a french forum.
A guy who apparenlty has studied electronics was in the "delay camp".
I asked him to give a numeric value of what he called a delay. No answer.
But he protested, without giving any further explanation about his point of
view, when I said he was doing an incredible amalgam between delay and phase
shift...
I think the confusion comes from the fact that phase shift can be considered as
an angular delay.
~~~~~~~~ Forr
§§§
"The time resolution of the ear is at best, about 10 mS.
[...]
Audio signals have a finite rise time (my data indicate
that the fastest audio signal coming from a microphone
is about 10 mS)"
Ooops ! sorry, MIKEB, I mean : 10 µS, in both cases.
LUMANAUW
"If an amp having signal passing more of this B junction, you will get more
delay, because these capacitance have to be charged/discharged."
This is a demonstration of how to make myths grow in audio.
(note : not every body agrees that the cited amplifiers are audibly the best).
EVA
"The output of any RC circuit reacts inmediately to input changes but with
non-constant time-dependent amplitude, as opposed to what happens when a signal
is delayed, where any change in the input appears at the output after some time.
Since any input change is not delayed in RC circuits, the output is just
reflecting the instantaneous value of the input signal with time-dependent
attenuation."
This is the most understandable explanation of the whole story.
Curiously, there was an idnetical discussion a few weeks ago on a french forum.
A guy who apparenlty has studied electronics was in the "delay camp".
I asked him to give a numeric value of what he called a delay. No answer.
But he protested, without giving any further explanation about his point of
view, when I said he was doing an incredible amalgam between delay and phase
shift...
I think the confusion comes from the fact that phase shift can be considered as
an angular delay.
~~~~~~~~ Forr
§§§
MBK said:
MBK,
I think you yourself quite clear. Some points:
- I don't think wwe have a terminology problem here, it is more that people are sloppy using clear terminology, sorry but the terms are quite clear. Even the term "time delay" often used is a funny one - we are NOT delaying time, are we? Yes, you may say, but anybody understands what we mean. Well, I dont think so. That is the basic problem.
- I think you misinterpreted Eva. (Unless I do😉 ). In his view, delay is when the effect of a cause appears some time after the cause. Like you post a letter at the post office, and the letter arrives a day later. In contrast, a signal going through a complex network appears at the output at the same instant it is inserted at the input. Some specific attributes may appear later, like the amplitude maximum or zero crossing. The output signal does no longer look esactly like the input signal of course, it is linearly distorted, but it is there from the first instant.
I suspect but are not fully sure that what you refer to as delay through an amp is actually phase shift and linear distortions decribed above. There is no delay in the sense that now there is an input signal and some time later the output appears; they are both there at the same time.
Inn the same manner, feedback that is often described as coming after the fact, is always there at the moment the error is there. But it is phase shifted (all amps have phase shift), and that causes linear distortion and therefore the error is not completely corrected.
Jan Didden
MBK said:
Well, i didn't believe that either...
So, once i needed to know and applied the wildest phasehifts
via FFT to a musicpiece... I might be deaf, but i heard no difference.
It seems that the ear is insensitive to phaseshift of harmonics inside a
signal, but extremely sensitive to phaseshifts/delays between left/right...
Mike
Eva,
the RC circuit, as every BW limited circuit, introduces time delay. The time delay in time domain is exactly T = RC for the simple RC integrating circuit.
You have to take this into account when you build multi-channel data acquisition system and you need to read values of many channels in the same time of sampling ....
Try to distinguish between a point of view in frequency domain and in the time domain. Though they are dual, you have to understand each other.
the RC circuit, as every BW limited circuit, introduces time delay. The time delay in time domain is exactly T = RC for the simple RC integrating circuit.
You have to take this into account when you build multi-channel data acquisition system and you need to read values of many channels in the same time of sampling ....
Try to distinguish between a point of view in frequency domain and in the time domain. Though they are dual, you have to understand each other.
Hi PMA !
I think Eva tried to point out that there is a big difference between
phaseshift and timedelay. If you pass a sine through a RC, it looks
like timedelayed, but when you pass a squarewave through the
same RC, you see the naked truth, phasehifts only, the transient
responds without any timedelay.
Mike
I think Eva tried to point out that there is a big difference between
phaseshift and timedelay. If you pass a sine through a RC, it looks
like timedelayed, but when you pass a squarewave through the
same RC, you see the naked truth, phasehifts only, the transient
responds without any timedelay.
Mike
MikeB said:
I tried the same and DID hear a difference. All you need is to adjust phase shift to be 'very quickly' lowering somewhere in range of several kHz. You've surely not tried the 'wildest'. The slope should go several times over the threshold of 360deg. You will definitely hear the trebles are delayed.
regards
Hmm, but by adjusting "very quickly" phaseshifts, didn't you create
dynamic phaseshifts ? These would audible as they create harmonics.
I used chaotic shifts from -360° to +360°, but constant.
Mike
dynamic phaseshifts ? These would audible as they create harmonics.
I used chaotic shifts from -360° to +360°, but constant.
Mike
MikeB said:
... and you can calculate the transfer function from the step response 😉 . This is well known, as well as another fact:
let sinewawes of different frequencies pass through RC integrating circuit. Transition of the RC output voltage through zero line will be always shifted (delayed) of dT = RC, behind the original (input) voltage. For low frequencies, this dT will be negligible compared to 1/f (period of sine wave). As sine wave frequency increases, the dT will get closer to 1/f and we can see the time delay (which is always the same). And we can calcute phase characteristics (phase shifts) for individual frequencies from the ratio of dT to 1/f. We have phase characteristics (frequency dependent phase angle), but time delay (dT = RC) has not changed 😉
Yes, as the phaseshift is frequencydependent it acts like a timedelay,
isn't this called "groupdelay" ?
It's just that a timedelay would not change the signal itself, only
delay it, this is same for a single sinewave, but not for complex signal.
Such a real timedelay would be introduced by long wires or digital
processing, not by RC or RL.
isn't this called "groupdelay" ?
It's just that a timedelay would not change the signal itself, only
delay it, this is same for a single sinewave, but not for complex signal.
Such a real timedelay would be introduced by long wires or digital
processing, not by RC or RL.
- Status
- Not open for further replies.