Suppression of pipe harmonic modes, mostly. Keeping things simple, end-loading a pipe applies maximum excitation of both the line fundamental and the harmonic modes. Shifting it further along the pipe (personally I favour a ratio based on length and cross-section, although length is most commonly used) will reduce the excitation of the fundamental to an extent, but also minimise excitation of the lower harmonics. F3 & F5 are typically most significant, as they are the hardest to damp out; HF harmonics by comparison with their short wavelengths are reasonably easy to suppress.
My point is that the only "benefit" you can show is a partial (half) reduction of the motional impedance peak. If that is desirable I can add 2 or 3 electrical components that do a complete job.
Yes, I've used "plain wave tubes" for testing compression drivers. This ideal resistive load confers you no benefit. It is on the backside of the driver so it doesn't contribute to some improved radiation or higher efficiency as an ideal horn on the front side of the driver might. The fact that the driver output is unchanged is proof that it is an inconsequential loading of the driver.
All explanations of TL goodness start with the ideal of waves emanating off to infinity to never come back, or proclaimed resistive, non-reactive, driver loading. From there we take the practical step of cutting the line short and tuning it to the drivers fundamental resonance. When Olney was doing this with drivers with a Q greater than 1, then he might have achieved something hard to get otherwise. The modern reality is that closed end pipes with enough damping to kill the line resonances are, in the end, just another sealed box enclosure.
David
scottmoose, wd placing the driver 15% down the line mean an overall longer line length, or wd it stay the same?
And my point is that not everyone is inclined to do so. You are advocating an electrical solution to an acoustic problem. Fair enough, it's one way (please also note I clearly said the pipe I displayed above is sub-optimal). Alternatively, one can use an acoustic solution to an acoustic problem. Both proceedures are perfectly valid; if you don't like one, or are obliged to use one means over another for x reason, fair enough, but it's a matter of preference and / or circumstance, and does not render the alternative invalid. They both work well.
Likewise.
Yes, I noticed that it was a back-load (and a sealed one at that). As noted, it's what it does to the impedance that's relevant / the objective when employed as a midrange line.
FYI, most of Olney's lines were open (as in 1/4 wave) pipes tuned to 1/2 wavelength of the driver's Fs, not sealed (as in 1/2 wave) pipes. Combined with many of the relatively underdamped drivers and high output Z amps common to the era, they would indeed damp out an otherwise heavily peaking Fb, but their additional purpose, as stated in his various articles (e.g in Electronics, JASA) and patent, was to extend the useable LF range of the system, which they did most effectively.
Well, as I've already demonstrated the contrary, and you accepted the fact that they are indeed different, you appear to be contradicting yourself.
Last edited:
Edit -actually, in my draft I said the pipe was sub-optimal, but that got lost in the final. Apologies, my bad.
The same. You're just tapping the driver into the pipe at x distance from the throat. Generally, it's at its most relevant for 1/4 wave pipes though (as in pipes sealed at the throat and open at the terminus), and particularly those where you're using pipe output to support the LF region. For aperiodic TLs, or 1/2 wave pipes (as in pipes sealed at both throat and terminus), it's less of an issue as pipe output is negligable / non-existant.
The same. You're just tapping the driver into the pipe at x distance from the throat. Generally, it's at its most relevant for 1/4 wave pipes though (as in pipes sealed at the throat and open at the terminus), and particularly those where you're using pipe output to support the LF region. For aperiodic TLs, or 1/2 wave pipes (as in pipes sealed at both throat and terminus), it's less of an issue as pipe output is negligable / non-existant.
Last edited:
Hmmmmm? I posted a response but it's not here. I think I must not have been logged in last time and didn't realize it; thus, my post didn't actually make it.
If you'll grant that my skills using Martin King's MathCad-based modeling worksheets (software) are adequately accurate, the accuracy of my modeling is the same as the accuracy of Martin's work, which was very similar to that of Augspurger regarding building experimental lines and measuring their performances, and Martin has continued to improve and evolve his worksheets for the last 10+ years. Others whom have posted in this thread can vouch that the same line modeled with both George's and Martin's software give virtually identical results. Martin's developmental work clearly showed that stuffing has smaller and smaller effects as frequency is decreased. The speed of sound would have to be decreased significantly in order for 20-30% changes, like at the much higher frequencies you cited, to occur at much lower frequencies, and that simply does not happen. Increasing a line's length, like making it non-tapered but with the same 1/4-wave resonant frequency as in an equivalent tapered line while placing stuffing in the same percentage of that length (like the first 2/3 of the line in my modeling examples), will not change this outcome.
Paul
If you'll grant that my skills using Martin King's MathCad-based modeling worksheets (software) are adequately accurate, the accuracy of my modeling is the same as the accuracy of Martin's work, which was very similar to that of Augspurger regarding building experimental lines and measuring their performances, and Martin has continued to improve and evolve his worksheets for the last 10+ years. Others whom have posted in this thread can vouch that the same line modeled with both George's and Martin's software give virtually identical results. Martin's developmental work clearly showed that stuffing has smaller and smaller effects as frequency is decreased. The speed of sound would have to be decreased significantly in order for 20-30% changes, like at the much higher frequencies you cited, to occur at much lower frequencies, and that simply does not happen. Increasing a line's length, like making it non-tapered but with the same 1/4-wave resonant frequency as in an equivalent tapered line while placing stuffing in the same percentage of that length (like the first 2/3 of the line in my modeling examples), will not change this outcome.
Paul
Last edited:
Both you and Martin were trying to tell my why, based simply on speed of sound changes, the response artifacts couldn't change by the amount Augspurger showed. Please address why in Augspurger's tests they do vary by that amount.
Bumblebees can't fly?
Hint, Augspurger shows that, in addition to speed of sound effects, line stuffing acts as a low-pass filter with a corner that shifts down considerably with increased stuffing.
David
Actually, I don't see a motional impedance bump as an acoustic problem. That was my point in my first response to the original poster: Special design of an enclosure to flatten the impedance, especially with no regard to acoustic output, is a poor optimization choice.
Which is why I agree that open ended TLs have some benefit: They give slightly more acoustic output for a given excursion, as long as you can find a balance between bass output and resonance modes.
Still not seeing any benefit to closed TLs.
Beyond that our arguments are getting a bit repetitive.
Merry Christmas All!
David
And compliments of the season to you & yours (& to everyone else).
Designing a cabinet to flatten the impedance is not a poor optimization choice. You might regard it as such, but that's your opinion only. If any cabinet intended for hifi duties is designed with no regard for acoustic output however, it is badly designed, if one could even use the word.
Quite. Fortunately, it's much easier for the majority of DIYers to achieve that these days thanks to the work of Martin, George etc.
From a technical POV, they are not necessarily beneficial in all cases (no universal applicability in this life); in some however, they're worth having. For e.g., if an amplifier isn't fond of reactive loads. Granted, you can argue that it's a rubbish amplifier on such a basis, but that only ever ends up in a dog-chasing-tail situation. And like them or no, they're one of the most effective means of damping the backwave available.
Designing a cabinet to flatten the impedance is not a poor optimization choice. You might regard it as such, but that's your opinion only. If any cabinet intended for hifi duties is designed with no regard for acoustic output however, it is badly designed, if one could even use the word.
Quite. Fortunately, it's much easier for the majority of DIYers to achieve that these days thanks to the work of Martin, George etc.
From a technical POV, they are not necessarily beneficial in all cases (no universal applicability in this life); in some however, they're worth having. For e.g., if an amplifier isn't fond of reactive loads. Granted, you can argue that it's a rubbish amplifier on such a basis, but that only ever ends up in a dog-chasing-tail situation. And like them or no, they're one of the most effective means of damping the backwave available.
The TL looks to be a good match with a current amplifier, the FR roll-off being complimented nicely by the smooth impedance rise at resonance.
dave
The stuffing will only be truly effective at frequencies where a full waveform can form in the box. That means that in a sealed box the damping can only be effective down to wl/2 = dimension of box.
dave
And below those frequencies resonances won't form and the box looks like a lumped parameter capacitor.
My point: we don't have to place the 1/2 wavelength dimensional resonance at the fundamental resonance of the woofer. We just want effective damping at whatever frequency the resonances are at.
David S.
Your argument regarding Augspurger's work actually supports Martin's and my position: You stated that Augspurger showed decreases in frequency of 400 to 300 Hz (25%) and 100 to 80 Hz (20%), which clearly indicate that as frequencies decrease, stuffing has less attenuation effect. If one wants to extrapolate to even lower frequencies, like 20-30 Hz, why would one not expect to see even less attenuation and lesser lowering of the frequencies from adding stuffing. The modeling I did showed that a line whose un-stuffed 1/4-wavelength resonant frequency was 27-28 Hz, exhibited just a bit more than a 10% decrease in that frequency, 24-25 Hz, when stuffing was added in the first 2/3 of the line at 1 lb/ft3.
Paul
Paul
Some graphs of experimental results on the decrease in fiber effectiveness as frequency is decreased here: The TLb -- Frequency Response
dave
Absorption
Rather than the endless philosophical back and forth, let me offer some facts about aborption of sound with fiberglass.
In architectural acoustics fiberglass is well known as one of the best, if not the best absorber of sound. Of course its effectiveness is a function of frequency depending on thickness. For anechoic chambers Beranek devised the standard anechoic wedge and found that a good design was highly absorptive for frequencies equal or above where its length was 1/4 wave long. So a 1 meter wedge is good to about 85 Hz. This was for a reflection of 10% of pressure, also stated as an absorption of 99% of the power.
For absorption on a wall, fiberglass will come in a variety of thicknesses and you choose a thickness based on what frequency you want effective absorption down too. Acousticians might quote 1" thick as good to 1kHz, 2" good to 400 and 3" good to 250 Hz.
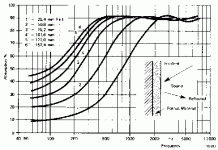
Attached is a diagram showing the measured absorption vs. frequency for a large variety of thicknesses. From this I would conservatively take the numbers that 1" is fully effective at 2000, 2" at 1000 and 4" at 500. Note that these tests show the material maxing out at an alpha of 0.9, meaning that going dramatically thicker than this doesn't buy you anything.
Lets compare the frequency of effectiveness to the thickness. With a speed of sound of 13,500 In/sec and 1" good to 2000 (2" to 1000 and 4" to 500 will give exactly the same numbers) we see that fiberglass generally gives full absorption when its thickness is 2000/13,500 or 1/6.75 wavelengths. This is conservative and still better than Beranek's 1/4 wavelengths figure.
Lets apply this to a cabinet. Pick any shape but have 10" from the driver to a reflective back wall. Since our cabinet, TL or not, will be 1/2 wave resonant, it is resonant at a wavelength of 20", so 13,500/20 = 675 Hz. What fiberglass depth do we need for absorption of that resonance and its harmonics? 20/6.75 = 2.96 inches. Call it 3" of treatment for effective absorption with a 10" deep cabinet.
Lets make the cabinet twice as deep or 20". So, 40" wavelength for first resonance at 13,500/40 = 338Hz. 40/6.75 for effective treatment = about 6".
Note that a 10" cavity is well treated by 3" of fiberglass, a 20" cavity by 6". See the pattern? All of these cabinets have fully effective absorption when the back wall is treated with 30% of the cabinets depth.
A fully stuffed TL is no longer a resonant device. (And thats a good thing.)
David
Rather than the endless philosophical back and forth, let me offer some facts about aborption of sound with fiberglass.
In architectural acoustics fiberglass is well known as one of the best, if not the best absorber of sound. Of course its effectiveness is a function of frequency depending on thickness. For anechoic chambers Beranek devised the standard anechoic wedge and found that a good design was highly absorptive for frequencies equal or above where its length was 1/4 wave long. So a 1 meter wedge is good to about 85 Hz. This was for a reflection of 10% of pressure, also stated as an absorption of 99% of the power.
For absorption on a wall, fiberglass will come in a variety of thicknesses and you choose a thickness based on what frequency you want effective absorption down too. Acousticians might quote 1" thick as good to 1kHz, 2" good to 400 and 3" good to 250 Hz.
Attached is a diagram showing the measured absorption vs. frequency for a large variety of thicknesses. From this I would conservatively take the numbers that 1" is fully effective at 2000, 2" at 1000 and 4" at 500. Note that these tests show the material maxing out at an alpha of 0.9, meaning that going dramatically thicker than this doesn't buy you anything.
Lets compare the frequency of effectiveness to the thickness. With a speed of sound of 13,500 In/sec and 1" good to 2000 (2" to 1000 and 4" to 500 will give exactly the same numbers) we see that fiberglass generally gives full absorption when its thickness is 2000/13,500 or 1/6.75 wavelengths. This is conservative and still better than Beranek's 1/4 wavelengths figure.
Lets apply this to a cabinet. Pick any shape but have 10" from the driver to a reflective back wall. Since our cabinet, TL or not, will be 1/2 wave resonant, it is resonant at a wavelength of 20", so 13,500/20 = 675 Hz. What fiberglass depth do we need for absorption of that resonance and its harmonics? 20/6.75 = 2.96 inches. Call it 3" of treatment for effective absorption with a 10" deep cabinet.
Lets make the cabinet twice as deep or 20". So, 40" wavelength for first resonance at 13,500/40 = 338Hz. 40/6.75 for effective treatment = about 6".
Note that a 10" cavity is well treated by 3" of fiberglass, a 20" cavity by 6". See the pattern? All of these cabinets have fully effective absorption when the back wall is treated with 30% of the cabinets depth.
A fully stuffed TL is no longer a resonant device. (And thats a good thing.)
David
Attachments
Hence a comparatively small amount of material provides absorption of cabinet resonance, however, what does it do to reflected sound coming back through the cone? Perhaps with a cabinet treated this way (eg, the 10" depth cabinet with 3" material providing suitable attenuation of the 675Hz resonance) a tone of say 300Hz may bounce from internal cabinet surfaces and exit back through the cone relatively un-attenuated and create a time smear?
A good question.
I think you are picturing a sharp wavefront emanating from the back of the driver to hit the fiberglass, with perhaps the LF part of that wavefront making it through the damping, bouncing off the rear wall and getting back to the cone.
If you buy the absorption curves I've shown then you'll agree that all energy from 675 Hz and up is effectivley absorbed by the 3" layer of fiberglass. Remember that the significance of 675 Hz was it was the first frequency where the propogation time was such that returning energy was 1 wave delayed, i.e. resonant. For frequencies below that the delay, in degrees of phase shift, becomes progressively less to the point of having no effect. Pressure thoughout the enclosure is the same and in-phase so the notion of an emanating wavefront isn't appropriate. At lower frequencies the enclosure is just a lumped parameter capacitor (volume compliance).
Viewed another way, the wavefront is robbed of all sharpness and the remaining LF part has inconsequential phase shift. This is seen in your previous response curve where the curve differences start at the first resonance. Below that frequency there are no abberations so there is nothing to damp. An offshoot of this is that a cabinet used well below its first resonance (say a subwoofer of large dimensions) gains nothing from stuffing (apparent volume increase or Qm changes aside).
David S.
p.s. Your impulse response just misses out on showing the interesting part. With a 320Hz first resonance you should see a significant reflection at 106cm delay, just outside your plotted area.
Last edited:
For a given line length stuffing acts as a low pass flter with more loss at high frequencies than low. This does not imply that longer lines can't be damped simply because there will be proportionately longer lengths of treatment. To the contrary, Augspurger states that longer lines need less stuffing density:
"Common sense suggest that a 100-Hz short pipe should have the same stuffing density as a 50-Hz pipe twice as long. In reality, test results clearly demonstrate that the shorter pipe requires greater packing density for equivalent performance."
"If the length of the pipe is doubled without changing its cross-sectional area...damping per unit length must be halved."
David S.
Well, I see we finally agree on one thing! As far as the rest goes, while I don't necessarily disagree with the quote from Augspurger, comparing a 100-Hz line to a longer 50-Hz line ends up with me thinking, "and your point is? Assuming we're talking only about a non-tapered line, the 1/4-wave resonant frequency from its length (and stuffing density and CSA) would presumably be optimized for a specific driver. Placing that same driver in a significantly shorter or longer line would not result in equally optimum performance, no matter the stuffing or CSA. Yes, you could stuff the life out of one or the other to minimize the damage, but if you're going to stuff the whole line to just emulate a sealed box, why build a TL in the first place? Now if we're talking about a tapered line, the length could be doubled (or halved) and the taper could be reduced (or increased) proportionally, keeping the same net volume, and you'd end up with equally good performance. Also, if you make the line shorter and increase its taper ratio, you can now use a lower stuffing density, while stuffing the same proportional length of line, because the bigger taper will reduce those pesky odd-harmonic dips and peaks in the response.
Paul
Paul
- Status
- Not open for further replies.