from recollection I measured it at 100R in the board, but I suppose my memory could be flakey!
I have measured the resistance from 1>3 and 1>6, 1>9 etc and the resistance is in the region of 51-58R
All measurements are at the valve base with the valve removed.
by my logic this looks like the 24R are in the region of 25-28R (they are currently 1/4W Allen Bradley that do wander...
As these are all with the valve removed then with the Valve back in place its 107R Cathode to earth.
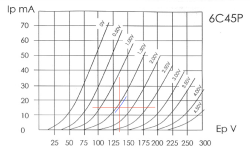
I guess this means I am running at 15mA Bias
I have measured the resistance from 1>3 and 1>6, 1>9 etc and the resistance is in the region of 51-58R
All measurements are at the valve base with the valve removed.
by my logic this looks like the 24R are in the region of 25-28R (they are currently 1/4W Allen Bradley that do wander...
As these are all with the valve removed then with the Valve back in place its 107R Cathode to earth.
I guess this means I am running at 15mA Bias
Attachments
I should have read the transformer datasheet more carefully. There are three different versions of the LL1660, the LL1660 PP, the LL1660/10 mA and the LL1660/18 mA. They differ in the core air gap and, hence, in the amount of DC current they can handle.
There is nothing wrong with that 15 mA if the transformer is an LL1660/18 mA. It can handle 18 mA while still having enough margin for the signal when connected with the four primary windings in series, like in connection Alt S.
Its inductance is specified as 100 H when connected in Alt Q, but in Alt Q, there are two windings with each 2.25 times as many turns as each of the four primaries in series, so 4.5/4 times the number of turns of Alt S. The inductance depends on the square of the number of turns, so
LL1660/18 mA connected as in Alt S:
Primary inductance (4/4.5)2 • 100 H ~= 79 H
There is nothing wrong with that 15 mA if the transformer is an LL1660/18 mA. It can handle 18 mA while still having enough margin for the signal when connected with the four primary windings in series, like in connection Alt S.
Its inductance is specified as 100 H when connected in Alt Q, but in Alt Q, there are two windings with each 2.25 times as many turns as each of the four primaries in series, so 4.5/4 times the number of turns of Alt S. The inductance depends on the square of the number of turns, so
LL1660/18 mA connected as in Alt S:
Primary inductance (4/4.5)2 • 100 H ~= 79 H
Recalculating the transfer, without auxiliary first-order high-pass filter:
Assuming that the transformer is indeed an LL1660/18 mA connected according to Alt S, the inductance is theoretically 79 H. I will round that to 80 H because the DC current is a little below the specified value.
The capacitor appears to be across the 100 Ω, and there is about 7 Ω undecoupled between the capacitor and the cathode. The valve is biased at 15 mA. Its transconductance is specified as 45 mS typical at 40 mA.
If the valve follows Child's law, its transconductance increases with the third power root of the current. Reducing the current from 40 mA to 15 mA then reduces the transconductance from 45 mS to 32.45 mS. The undecoupled part of the cathode resistor gives some series feedback that effectively reduces the transconductance to 1/(7 Ω + 1/32.45 mS) ≈ 26.44 mS.
Filling in the updated cathode resistor value (100 Ω, the part that gets decoupled), the updated inductance and the updated transconductance and trying all E3 values from 22 μF to 2200 μF for the decoupling capacitor, my spreadsheet gives these plots:
22 μF:
47 μF:
100 μF:
220 μF:
470 μF:
1000 μF:
2200 μF:
Take your pick...
Assuming that the transformer is indeed an LL1660/18 mA connected according to Alt S, the inductance is theoretically 79 H. I will round that to 80 H because the DC current is a little below the specified value.
The capacitor appears to be across the 100 Ω, and there is about 7 Ω undecoupled between the capacitor and the cathode. The valve is biased at 15 mA. Its transconductance is specified as 45 mS typical at 40 mA.
If the valve follows Child's law, its transconductance increases with the third power root of the current. Reducing the current from 40 mA to 15 mA then reduces the transconductance from 45 mS to 32.45 mS. The undecoupled part of the cathode resistor gives some series feedback that effectively reduces the transconductance to 1/(7 Ω + 1/32.45 mS) ≈ 26.44 mS.
Filling in the updated cathode resistor value (100 Ω, the part that gets decoupled), the updated inductance and the updated transconductance and trying all E3 values from 22 μF to 2200 μF for the decoupling capacitor, my spreadsheet gives these plots:
22 μF:
47 μF:
100 μF:
220 μF:
470 μF:
1000 μF:
2200 μF:
Take your pick...
Try to recalculate it with loaded secondary (as about 20k secondary load transferring to primary side).
LL1660 has -enough large- bump at HF without Zobel, or appropriate load.
In these case even few hundred uF may "enough".
LL1660 has -enough large- bump at HF without Zobel, or appropriate load.
In these case even few hundred uF may "enough".
A triode has very little distortion with infinite load impedance, maybe that is what is meant. If so, I'm not sure it is very relevant, as the second stage probably dominates the distortion anyway.
You have a peak (+4dB at 80Hz). I usually set the resonant peak at about 15Hz if that is possibile. You can set it higher and get a genuine bass booster, not the usual treble cut like in guitar amplifiers. It depends what matters to you.
Very nice spreadsheet MarcelvdG!
An inductor or unloaded transformer acts as an AC constant current source (CCS) at not too low or too high frequencies.
You're right.
Was just speculating why the amp uses an unloaded interstage transformer at all.
Yes, that's the performance I'd expect. What primary capacitance did you assume?
My question is, why use an interstage transformer at all? Any transformer limits the bandwidth.
Just to avoid a coupling cap or something else?
Marcel, this is indeed excellent work - thank you so much 🙂
Filenet, I have voiced the system with this peak here so would prefer not to change it.
I like a richer, fuller sound (than is probably correct) so I guess this works in my favour !
Rich
Filenet, I have voiced the system with this peak here so would prefer not to change it.
I like a richer, fuller sound (than is probably correct) so I guess this works in my favour !
Rich
I have no idea why the interstage is designed like this, as per the previous posts this is not my design, and the author of the design is not open-minded about sharing his knowledge/secrets/designs :-(
There is some information about high-frequency peaking in the datasheet tonescout linked to, https://www.lundahltransformers.com/wp-content/uploads/datasheets/1660.pdf , but it is very incomplete and unclear. Jensen usually specifies some RC network that prevents peaking, but this Lundahl datasheet only says:
"The source impedances used in
the tables indicates a recommended
upper limit, unless freq. response can
be compromised.
At lower source impedance resonance
peaking will occure. It can be
reduced using secondary load resistors."
"The source impedances used in
the tables indicates a recommended
upper limit, unless freq. response can
be compromised.
At lower source impedance resonance
peaking will occure. It can be
reduced using secondary load resistors."
Capacitors vs interstage transformers have advantages and disadvantages.
I guess some prefer one or the other because they sound differently.
Attached is a zip file with the report extended with a section about LR parallel networks as load and with a modified spreadsheet. The effect of a 27 kohm load on the secondary side of the transformer is very small for big capacitors (as was to be expected, it is mainly the valve doing the damping then). For small capacitors, it helps to damp the resonance, but you still get a bit of a hump due to the wrong zero location (if you have no auxiliary filter to correct for that).
Mind you, I only look at the low-frequency response, not at humps at high audio frequencies.
Mind you, I only look at the low-frequency response, not at humps at high audio frequencies.
In the 1920's, mainly to reduce the number of valves, reduce the required supply voltage and improve battery lifetime.
Thanks, but I meant the amp here.
HF response might be poor depending on transformer primary capacitance (i.e. self-resonance).
And the IST looks expensive.
Hoping to learn something.