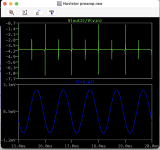
What I wanted to do is: plot -Vin-Vout/gain.
-Vi changes the phase; I subtract the output devided by gain.
If I look at what I do - I understand I never got higher than 6 or 7 for math . . . Vout/(vout/vin)= 1/vin ???? Even though many years ago I passed exams in which I had to calculate de Broglie Wave Equation; and several statistics exams.
-Vi changes the phase; I subtract the output devided by gain.
If I look at what I do - I understand I never got higher than 6 or 7 for math . . . Vout/(vout/vin)= 1/vin ???? Even though many years ago I passed exams in which I had to calculate de Broglie Wave Equation; and several statistics exams.
I'm not sure whether -Vin-Vout/gain is a usefull quantity. What would it represent?
Assuming that gain = Vout/Vin, it comes out to -Vin-Vin = -2*Vin.
Unless you meant (-Vin-Vout)/gain which would come out to (-Vin-Vout)*Vin/Vout = -Vin^2 -Vin = Vin (-Vin-1).
Jan
Assuming that gain = Vout/Vin, it comes out to -Vin-Vin = -2*Vin.
Unless you meant (-Vin-Vout)/gain which would come out to (-Vin-Vout)*Vin/Vout = -Vin^2 -Vin = Vin (-Vin-1).
Jan
Thanks, here my thinking:
To me, the Vout/gain would represent a wave that is as large as the input; so subtracting it from the input again should give zero nada. But there will be a difference.
I think then: The residual of Vin-Vout/gain is the harmonics and phase shift.
To subtract, I need to put Vin in the inrse phase because otherwise the two add up. . . So manually it works (see the 3,85) I compared the two voltages by hand - approximated by testing small difference between 3.8 and 3.9 in the measured data - then went for lowest figure - the way I my distortion meter works too. This takes a lot of time of course.
To me, the Vout/gain would represent a wave that is as large as the input; so subtracting it from the input again should give zero nada. But there will be a difference.
I think then: The residual of Vin-Vout/gain is the harmonics and phase shift.
To subtract, I need to put Vin in the inrse phase because otherwise the two add up. . . So manually it works (see the 3,85) I compared the two voltages by hand - approximated by testing small difference between 3.8 and 3.9 in the measured data - then went for lowest figure - the way I my distortion meter works too. This takes a lot of time of course.
- I think it is better to take this to the large thread on how LTSPICE works ??

I don't see how there can be a difference between ' Vin' and ' Vin' .
The gain is by definition Vout/Vin, so if you measure Vout/Vin you by definition have the gain.
This gain is a complex quantity having a magnitude and phase and differing with frequency and also with level (distortion).
Why don't you plot Vout/Vin, that'll show you gain, warts and all.
Jan
The gain is by definition Vout/Vin, so if you measure Vout/Vin you by definition have the gain.
This gain is a complex quantity having a magnitude and phase and differing with frequency and also with level (distortion).
Why don't you plot Vout/Vin, that'll show you gain, warts and all.
Jan
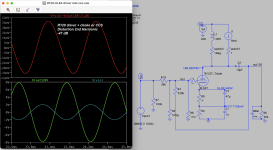
... and that is how crossover distortion looks: sharp deviations from the nominal gain at crossover.
Nice plot. It may not be 100% realistic, as the spice models are not either, but it's a nice illustration.
Jan
Nice plot. It may not be 100% realistic, as the spice models are not either, but it's a nice illustration.
Jan
Looks like a transistor cross-over. (BC547>>??) But it is not 'real' to me. :🙂
The bottom trace is the cathode that I try to null to -50 or even 70 dB.
The bottom trace is the cathode that I try to null to -50 or even 70 dB.
The problem is that you ask the simulator to handle a division by zero at the zero-crossing instants. This is a problem, unless it is specifically addressed in the soft. We, as human can handle intellectually infinitesimal quantities or infinites: we can even distinguish different types of infinity (like ∞<∞²), etc. but unless the soft is designed to handle it, it will give incoherent results.What I mean is really Vout/gain-Vin should be zero else gives the distortion. . . I hardly recognize this.
Anyway: the warts . .
View attachment 1075389
In the boundary regions, the accuracy will decrease according to the number of digits, rounding method, etc., until it breaks down completely at the singularity
ahh, thanks that is an unsolvable problem then the way I started out.
Leaves me with the question: I saw a simulation, in which a constant 'GAIN' was used by dividing an otcome with that calculated Gain.
Leaves me with the question: I saw a simulation, in which a constant 'GAIN' was used by dividing an otcome with that calculated Gain.
- How else calculate can we it and re-use the outcome in another calculation?
Infinity is infinity: there are no different types of infinity. Infinite means unbounded, bounds either exist or they don't. Infinity is not a number; it is a limit. For instance, does it make mathematical sense to ask:we can even distinguish different types of infinity (like ∞<∞²)
a) Is infinity prime?
b) Is it even?
c) How many multiples does it have?
These questions are meaningless/ridiculous because infinity is not quantisable. However, asking the same questions regarding any (finite) number they make sense.
Let us do some thought experiment to illustrate that infinity is not graded and that there is only one infinity.
Let us consider whole numbers starting from -infinity to +infinity. Let us now now create the sets containing even numbers:
Even = {...., -6, -4, -2, 0, 2, 4, 6, ....}
Multiples of 3 = {....., -6, -3, 0, 3, 6, ....}
Multiples of 5 = {....., -5, 0, 5, ......}
Multiples of 1000 = {....., -1000, 0, 1000, .....}
The sets have been created by choosing numbers from the number line. Examining the sets one finds that in set "Even" numbers occur more frequenty compared with "Multiples of 3", and so on. This would imply the sets are less infinite compared with the original set, but this is false, because a function can be defined which maps numbers from the number line to any chosen set.
The function would be as follows(for one set):
Code:
fn: number line -----> Even
f(-3) maps to -6
f(-2) maps to -4
f(-1) maps to -2
f(0) maps to 0
f(1) maps to 2
f(2) maps to 4
f(3) maps to 6
And so on, on both ends.This is a one-to-one and onto function which implies the count of the numbers in the set "Even" is as big as the count of numbers on the number line.
No it does not, they are obviously not the same. But if you would say that both sets are infinite I'm with you.which implies the count of the numbers in the set "Even" is as big as the count of numbers on the number line.
Jan
There is a surjection (a one-to-one) function from the number line to the set even. That proves they have the same size, otherwise such a surjection fails. I know, this appears odd.
Even though infinity x infinity appears it must be bigger, a function can be defined to map every element in the Integer Domain onto every element in a 'square' matrix of size infinity. Let us take ourselves in the 'middle' of such a square matrix, and let us denote every element by two coordinates. So, we start from the origin. Let us start with the element at (0, 0), now we move on to element (1,0), move up to (1,1), turn to the left to (0,1), move to (-1, 1), turn down to (-1, 0), move to (-1, -1), turn to the right to (-1, 0) and to move to (-1, 1). That way we traced all points around (0,0). Next we trace round the trace we just did. In this way, a function can be defined to map every element in the Integer Domain to every point in the matrix which is made of infinity x infinity.
This function proves that infinity x infinity is as big as infinity.
This function proves that infinity x infinity is as big as infinity.
Cantor proved that there are more real numbers than integers.
The infinite set of real numbers has more members than the infinite set of integers.
Wikipedia discusses it under the title "Cantor's diagonal argument".
The infinite set of real numbers has more members than the infinite set of integers.
Wikipedia discusses it under the title "Cantor's diagonal argument".
Integers are real numbers, so they are part and parcel of the same set. It is a common misconception that infinity is graded, but this contradicts its very nature of unbountedness. Surjections are a powerful tool to show/prove that a set that appears to have more elements is as infinite as another set appearing to have less elements.
Rigarding consulting Wikipedia, I know that university students are not allowed to quote it. If they do, they are penalised. The reason is Wikipedia is often vandalised. I never consult it; it is far better to buy a book from a reputable source.
Rigarding consulting Wikipedia, I know that university students are not allowed to quote it. If they do, they are penalised. The reason is Wikipedia is often vandalised. I never consult it; it is far better to buy a book from a reputable source.
Let us define a function which maps integers onto decimal numbers with one digit after the decimal point. (This can be extended to any number of decimal places. The proof would be extendable to all real numbers by induction.)
The above can be used to span numbers up to infinity BOTH in the domain and codomain. The domain never runs out of elements notwithstanding it appears to have less elements.
Again, this shows infinity is NOT graded.
Code:
F(1):1 ---> 1.0
F(2):2 ---> 1.1
F(3):3 ---> 1.2
F(4):4 ---> 1.3
F(5):5 ---> 1.4
.....
F(n):n ---> 0.1*n + 0.9The above can be used to span numbers up to infinity BOTH in the domain and codomain. The domain never runs out of elements notwithstanding it appears to have less elements.
Again, this shows infinity is NOT graded.
I have unwittingly opened a huge can of worms, and touched a raw nerve at the same time. I am not a mathematician, but I use maths, and distinguishing between different varieties of infinity (or zero) can be useful to solve indetermination in problems.
Most people seem to agree that infinities come in grades, but of course there is only one symbol for all, and to solve indetermination problems, you need to know where they come from.
With good programming, a soft can certainly resolve these kinds of problems too. In the case of LTspice, there must be a workaround, like using the derivatives or something similar (hoping I am not making another mathematical faux-pas!)
Most people seem to agree that infinities come in grades, but of course there is only one symbol for all, and to solve indetermination problems, you need to know where they come from.
With good programming, a soft can certainly resolve these kinds of problems too. In the case of LTspice, there must be a workaround, like using the derivatives or something similar (hoping I am not making another mathematical faux-pas!)
Funny, I have no problem with determining the loop gain with LTSpice. Here we are pondering the ramifications of ’different‘ kinds of infinity and all I have to do is plot Vo/Vx and I have my loop gain.
- Home
- Amplifiers
- Solid State
- Calculating open loop gain using LTSpice