Hello Brian,
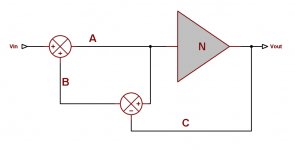
I wish I could put the 'essence' of Hec in mathematical form; I don't know how to do it. It has to do with your last diagram where you split off the two loops, using a for the pfb loop and b for the nfb loop. This diagram is only a correct representation of the original Hec circuit when a=b, the loops are not independent. In the original circuit, both are scaled by the same scalar, which is the binding element.
Lets go back to basics. See the attached.
You maintain that to investigate the loop, you cut it at point C. By definition, you thus maintain that cutting the loop for investigation at point A or B is incorrect.
I maintain that to investigate the Hec circuit you should cut the loop at point A or point B. By definition I thus maintain that cutting the loop for investigation at point C is incorrect.
As long as we have this opposing views, there will not be a common model or a common transformation, and these views cannot be reconciled.
I don't know what else to discuss, possibly we have reached the end of the line here, unless you see a way out.
Edit: we xposted...
Jan Didden
I wish I could put the 'essence' of Hec in mathematical form; I don't know how to do it. It has to do with your last diagram where you split off the two loops, using a for the pfb loop and b for the nfb loop. This diagram is only a correct representation of the original Hec circuit when a=b, the loops are not independent. In the original circuit, both are scaled by the same scalar, which is the binding element.
Lets go back to basics. See the attached.
You maintain that to investigate the loop, you cut it at point C. By definition, you thus maintain that cutting the loop for investigation at point A or B is incorrect.
I maintain that to investigate the Hec circuit you should cut the loop at point A or point B. By definition I thus maintain that cutting the loop for investigation at point C is incorrect.
As long as we have this opposing views, there will not be a common model or a common transformation, and these views cannot be reconciled.
I don't know what else to discuss, possibly we have reached the end of the line here, unless you see a way out.
Edit: we xposted...
Jan Didden
Attachments
Good afternoon.
Here's the crux. The diagram is functionally identical to original HEC when a=b, but this does not strike me as a special condition. To me, even when a != b, the system still does the same basic thing; it is just that the system gain is altered. IOW I see the separation of a and b scalars leads to a more generalized form of HEC.
Perhaps we can agree on what can be learned from the different cut points. I think we agree that C is where the global NFB loop behaviour can be examined. To me, this is the most important examination because it reveals the "correction power" and the system stability. It is the control loop.
My wording is often clumsy. I am not saying it is incorrect to measure at A or B per se...I am am saying that it is incorrect to examine the global NFB loop at A or B. I think you agree? But I don't understand what you are trying to examine by cutting at A or B. If I was able to understand this, I might be able to get closer to your view.
Brian
janneman said:
Here's the crux. The diagram is functionally identical to original HEC when a=b, but this does not strike me as a special condition. To me, even when a != b, the system still does the same basic thing; it is just that the system gain is altered. IOW I see the separation of a and b scalars leads to a more generalized form of HEC.
Perhaps we can agree on what can be learned from the different cut points. I think we agree that C is where the global NFB loop behaviour can be examined. To me, this is the most important examination because it reveals the "correction power" and the system stability. It is the control loop.
My wording is often clumsy. I am not saying it is incorrect to measure at A or B per se...I am am saying that it is incorrect to examine the global NFB loop at A or B. I think you agree? But I don't understand what you are trying to examine by cutting at A or B. If I was able to understand this, I might be able to get closer to your view.
Brian
Brian, Jan.
There is no "correct" way for cutting the loop as much as this is not a classical single feedback topology. Perhaps - as I did some years back while working the subject - cutting at C exposes the infinite "cannonical" loop gain under perfect error cancellation conditions.
Yet, it must be reminded that to consider perfect error cancellation is moot and not only because of stability issues, which are at worst a byproduct.
What must be borne in mind is any realization of the summing nodes implies processing delay (even with ideal linearity which is also a prerrequisite), which in turn implies the zero cannot be achieved as long as one is trying to null the sum of a real and a complex term.
Regarding stability - which is frequently brought up as the killer issue - the situation is not worst than the one where classical loop gain is very high - which is at most what can be attained given the impossibility of cancellation as said above -.
This does not impy HEC should be dismissed because of lack of novelty. Is is - keeping due distance - similar to the historical controversy about the particle or wave nature of light.
Sometimes it is handy to look at light as particles, sometimes waves are better suited for the job, and while none is definitive (not even for particles themselves like electrons !!) using both points of view depending on circumnstances far from doing harm only provide better and useful insights.
Rodolfo
There is no "correct" way for cutting the loop as much as this is not a classical single feedback topology. Perhaps - as I did some years back while working the subject - cutting at C exposes the infinite "cannonical" loop gain under perfect error cancellation conditions.
Yet, it must be reminded that to consider perfect error cancellation is moot and not only because of stability issues, which are at worst a byproduct.
What must be borne in mind is any realization of the summing nodes implies processing delay (even with ideal linearity which is also a prerrequisite), which in turn implies the zero cannot be achieved as long as one is trying to null the sum of a real and a complex term.
Regarding stability - which is frequently brought up as the killer issue - the situation is not worst than the one where classical loop gain is very high - which is at most what can be attained given the impossibility of cancellation as said above -.
This does not impy HEC should be dismissed because of lack of novelty. Is is - keeping due distance - similar to the historical controversy about the particle or wave nature of light.
Sometimes it is handy to look at light as particles, sometimes waves are better suited for the job, and while none is definitive (not even for particles themselves like electrons !!) using both points of view depending on circumnstances far from doing harm only provide better and useful insights.
Rodolfo
ingrast said:
Wow. I must say I am surprised at you, Rodolfo, for introducing this wild sophistry into the discussion. For goodess sake...comparing it to wave duality!
This is a very simple system that is objectively describable using simple algebra. There are no quantum uncertainties at work. I think it is quite simple...but perhaps I am a genius like the late Richard Feynman.
The purpose of objective analysis is to keep us humble and to stop us from believing what we want to believe, rather than what is real. Jan's post tag-line quote from CH exemplifies this.
😎
traderbam said:
.....but perhaps I am a genius like the late Richard Feynman.
...
While the possibility of you being a genious should not be entirely dismissed 😉, I did not intend to imply quantum uncertainties on the HEC - GNF issue.
Assume you never really considered that as my intention either but took it as a playful lead for a joke.
Please note I was careful to remark "- keeping due distance - ", Iwanted to stress the concept of alternate contradicting viewpoints are not necessarily a curse but a benefit.
Rodolfo
ingrast said:
It is very open-minded of you not to entirely dismiss the notion! 😛
IMO, alternative views or hypotheses are ok provided they are not considered to be true until there is evidence to support them. Even if they are attractive ideas. Like Christopher Hitchens, I think we have to be careful not to unduly waste our valuable resources defending ideas for which there is no hard evidence. I wonder how short this thread would be if we had applied Christopher Hitchens rule to the debates?
While to waste valuable resources is undesirable in abstract, torturing ideas to inch forward in knowledge is less harmful than alternate favorite ways (read war, financial markets, overcomsumption, whatever) albeit small relief in the end.
Again I must stress I am not defending HEC against GNF but the alternance as concept or strategy viewpoints for an underlying construct.
This can be readily appreciated in my posts from the very begining of this controversy unless I was hopelessly obscure in this respect.
Rodolfo
PS Check here first
Again I must stress I am not defending HEC against GNF but the alternance as concept or strategy viewpoints for an underlying construct.
This can be readily appreciated in my posts from the very begining of this controversy unless I was hopelessly obscure in this respect.
Rodolfo
PS Check here first
Brian, Rodolfo,
Thanks for your intervention Rodolfo, it did help.
Let me try again to clarify my reasoning.
I understand there are different ways to look at a (this) system. In that sense, cutting the loop at C is as valid as cutting it at any other point.
I think we agree that cutting it either at say, A or at C, gives different views and different attributes of that particular loop we thus created. I agree that cutting it at C does expose the infinite gain loop.
Cutting it at A, for example, exposes other attributes. For example, it shows that the error reduction at low frequencies is limited to the accuracy of 'a' (and the input summer), in that an accuracy of 1% gives you a max error reduction of 40dB.
As another example, it shows you that if you want this 40dB reduction up to frequency fe, your 'a' should have its -3dB frequency at least 2 decades above fe.
These are attributes that can readily be verified in calculations or in actual hardware, and confirm teh results of analyzing the loop in that way. Surely the purpose of analyzing the loop is to gain insight in how the actual system behaves? I don't see how analyzing the loop as proposed by Brian, while possibly interesting as an academic exercise, tells me how my system will behave, with the examples shown as well as in other ways. Maybe that is my blind spot?
Jan Didden
Thanks for your intervention Rodolfo, it did help.
Let me try again to clarify my reasoning.
I understand there are different ways to look at a (this) system. In that sense, cutting the loop at C is as valid as cutting it at any other point.
I think we agree that cutting it either at say, A or at C, gives different views and different attributes of that particular loop we thus created. I agree that cutting it at C does expose the infinite gain loop.
Cutting it at A, for example, exposes other attributes. For example, it shows that the error reduction at low frequencies is limited to the accuracy of 'a' (and the input summer), in that an accuracy of 1% gives you a max error reduction of 40dB.
As another example, it shows you that if you want this 40dB reduction up to frequency fe, your 'a' should have its -3dB frequency at least 2 decades above fe.
These are attributes that can readily be verified in calculations or in actual hardware, and confirm teh results of analyzing the loop in that way. Surely the purpose of analyzing the loop is to gain insight in how the actual system behaves? I don't see how analyzing the loop as proposed by Brian, while possibly interesting as an academic exercise, tells me how my system will behave, with the examples shown as well as in other ways. Maybe that is my blind spot?
Jan Didden
Rodolfo, and others,
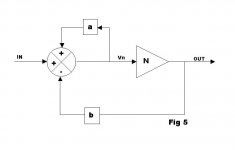
Do you agree or not that this diagram and equations are an accurate representation of the HEC concept? The original HEC being the special case when a=b.
Vout/Vin = N / (1-a+bN)
FB loop gain = -bN/(1-a)
FB factor = b
PS: If you do not agree, please justify your disagreement objectively. 🙂
Do you agree or not that this diagram and equations are an accurate representation of the HEC concept? The original HEC being the special case when a=b.
Vout/Vin = N / (1-a+bN)
FB loop gain = -bN/(1-a)
FB factor = b
PS: If you do not agree, please justify your disagreement objectively. 🙂
Attachments
Hi Jan,
I don't see your blind spot (pun intended).
The HEC topology (hope this at least will not be challenged) is different from GNF and one should not attempt to make cuts here or there and claim which is the right spot unless there is a purpose, and in case the purpose is to compare with GNF, then C is probably the more insightfull place but then again only for purposes of comparison with the familiar loop gain for GNF only.
Cutting at A as you propose, exposes something implicit in GNF but not in an obvious way.
In an ideal situation with active elements, gain and bandwith are "conjugate" attributes in a lousy sense, in that due to at least a 6 db/oct slope is unavoidable, then ultra high bandwith implies ultra high gain at DC and reciprocally.
So the fact that bandwith in the summing node for HEC rules, was to be expected in the real world.
Rodolfo
I don't see your blind spot (pun intended).
The HEC topology (hope this at least will not be challenged) is different from GNF and one should not attempt to make cuts here or there and claim which is the right spot unless there is a purpose, and in case the purpose is to compare with GNF, then C is probably the more insightfull place but then again only for purposes of comparison with the familiar loop gain for GNF only.
Cutting at A as you propose, exposes something implicit in GNF but not in an obvious way.
In an ideal situation with active elements, gain and bandwith are "conjugate" attributes in a lousy sense, in that due to at least a 6 db/oct slope is unavoidable, then ultra high bandwith implies ultra high gain at DC and reciprocally.
So the fact that bandwith in the summing node for HEC rules, was to be expected in the real world.
Rodolfo
traderbam said:
Though I did not bother to check, I will not make the offence of suspecting errors, guess you are proficient.
Question is, which is your point?
Rodolfo
ingrast said:
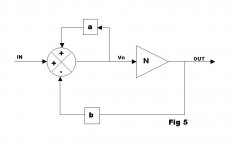
This diagram is what I define to be a GNF system. So based on your latest comment to Jan that HEC topology is different from GNF, and based on your earlier paper "why error correction is conceptually different from negative feedback?", I suppose I can only draw the conclusion that your definition of GNF must be different from mine.
If it is my definition of a GNF system that is wrong, then I must change it.
Attachments
traderbam said:
I'm afraid we're going around in circles, but here goes.
I agree that if you would have your circuit and the original Hec circuit each in a black box they would be indistinguisable.
I donot agree that the feedback factor is b. My reasoning is that there are two feedback paths to the input summer, so the feedback factor is a combination of the two. Since I am interested in how this system behaves from input to output, I need to consider the total, combined feedback from output to input, which IMO is the combined pos & neg fb loop.
Novel idea: maybe we don't really disagree that much. I agree that your way of looking at the circuit exposes the infinite gain. In my way of looking at the circuit, I see a feedback factor varying with plant gain, but not the infinite gain. I prefer my view because I can relate it directly to the actual behaviour of the hardware. You may prefer your view because it shows you circuit attributes that elude me.
Is this line of thought worth pursueing further?
Jan Didden
traderbam said:
The modified drawing of an EC topology as you presented is not what is universally accepted as a GNF topology.
For one, a classical GNF scheme as patented by Black reduces to an amplifier to be corrected, with a neutral summing block in front which only performs substraction of (a sample of) the output from the input before feeding to the amplifier.
If you subsume the inner loop of the EC topology so as to leave exposed the outer loop, the amplifier, and a new summing block with the added functions hidden inside, then its behavior is vastly different from that of the classic summing block, as it is also evident from the different transfer function.
Looking the circuit this way (subsuming the EC inner loop) then yes, it is not GNF as generally understood. (The input summer is different).
That in practice it can be treated as an equivalent feedback system, is also true of course.
Rodolfo
🙂janneman said:
Definition issue.
This is a feedback control system. A control system senses the difference (sometimes the ratio) between input (target) and output (sense) and tries to control it. The performance characteristics of the system are defined by the change in output in response to a change in the sense signal. The sense signal is at C.
Aside from implementation considerations of the input summer, what useful information does measuring the combined FB signal into the summer give you?
I make the combined FB signal into the summer of the HEC circuit = a.(Vin - Vout)/(1 - a)
Brian
some gains can be inspected without loop cutting, this example sim's voltage gain shows the limits of HEC are determined by the gain of the active circuits implementing the summers:
(we really did cover all of this long ago)
(we really did cover all of this long ago)
jcx said:
how about I measure the high differential gain with the circuit "put back together"?
This sort of measurement is practically difficult in the real world but Spice makes it easy to see my "abstact, theoretical" differential gain:
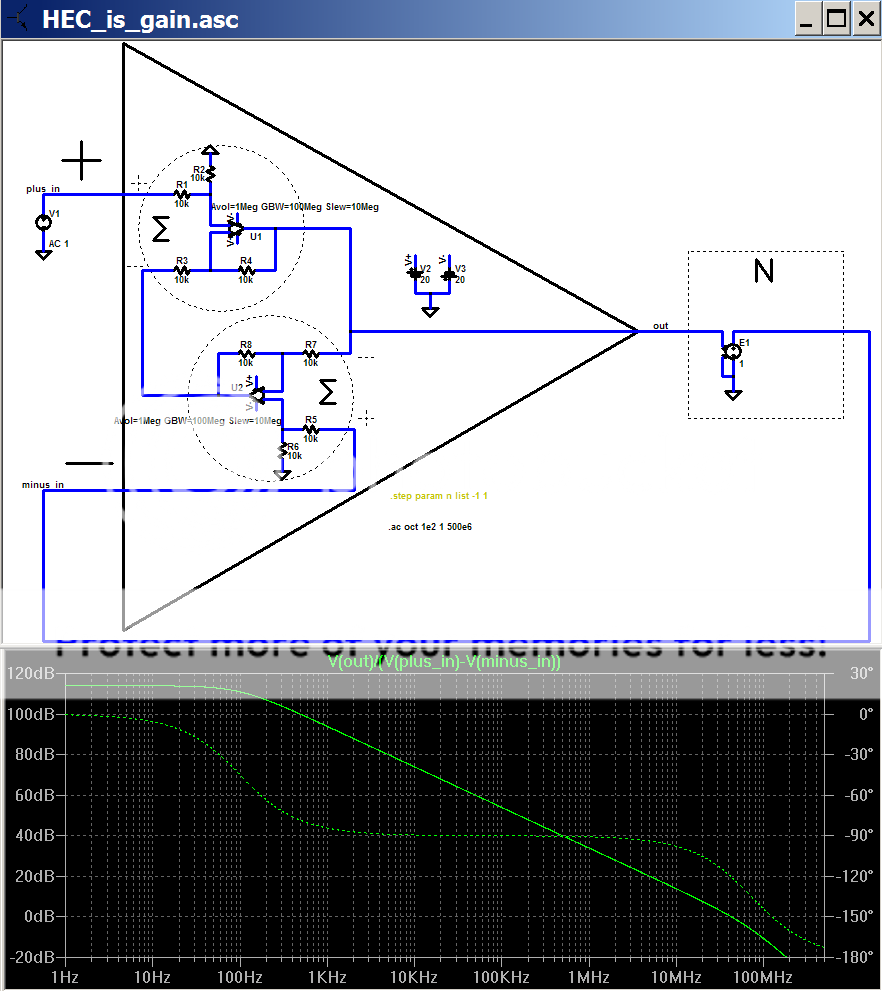
Did you miss Bob's comment that the "high gain" viewpoint is equally valid and therefore equally active and demonstrable when the EC circuit is working in full "EC" glory with internal node voltages that fit your sims of several pages ago with the "EC" heuristic explainations of this exact same circuit?
...
ingrast said:
Exactly.
If we would use analog computers today, then the HEC feedback model would really matter; e.g. different approaches could have wildly different convergence speeds.
But at the end of the day, who cares which is the best instrument to analyze this topology, if the results are consistent.
I guess the confusion is between FB as analysis instrument and FB as circuit topology. To me, as long as I can analyze the second without using FB theory, it doesn't really exist.
ingrast said:
Suppose I were to do the opposite of what you suggest and separate the inner loop from the input summer...it can have a separate summer to itself (the input summer feeds into the new summer). Now, the input summer is exactly like Black's.
According to your definition, is this HEC or is this GNF?
ingrast said:
I like this analogy. I find all three views useful in their own way. This latest discussion on cutting the loop and stability of HEC has been valuable and interesting.
I also like that you noted that real-world implementation delays and imperfections limit the distortion reduction achievable with both HEC and NFB. We should also throw feedforward error correction in there as well. Even though it can be perfect in principle and appears not to have stability issues, those same problems with real-world delay and matching limit its ability to reduce distortion. Its need for an output summer at a high-power point is also problematic.
Cheers,
Bob