I do. Funny you should ask, because just two weeks ago I spent several days listening to my MLTLs instead of my Revply flat panels, just to get a fresh impression. What struck me most was that with the MLTLs, if I was just a little too close to one of the speakers, I felt like all the sound was coming from that driver only. With the flat panels, even when you are very close to one of them, it never feels like the sound is coming directly from "right there".
Eric
I like minwax "wipe-on" polyurethane. But use as little as you can. The main issue is that any finish will add weight, which will reduce sensitivity. But I would also recommend coating both the front and the back. The reason is that coating only one side will allow moisture to enter (and leave) the uncoated side more easily than the other, making the panel more prone to warping. One key to avoid warping in wood composites is to treat both sides exactly the same.
Also, once you are sure where you want the exciter, you may want to put a few extra coats of finish just on that spot. It will provide a better surface for the exciter to bond to, and also strengthen the surface of the panel at that spot, so that if you ever have to remove the exciter, you will be less likely to damage the panel.
Eric
Sort of OT but some troubleshooting on my power amplifier indicates that the output-protection relay probably is the problem. The amp's idle current is fine, even after 30+ years. I did tweak its offset as part of the initial checkout after I re-capped it, and it hasn't moved.....so I don't think it's a problem with the amp itself. It's just the contacts on that ancient relay. This makes me happy.
I found a relay that is (mostly) a drop-in replacement -- I only need to add a 1 watt 1.2K series resistor, to account for the difference in the relay coils' resistance. That is mostly to reduce the power dissipation in the coil so it's within the manufacturer's max-specified limit.
The other thing is that I found several burned-out #47 incandescent bulbs in the VU meters. They still are easy to find because they're used by the zillions in pinball machines! I found some drop-in LED replacements so the old beast should be good for another 30 years 😆.
I found a relay that is (mostly) a drop-in replacement -- I only need to add a 1 watt 1.2K series resistor, to account for the difference in the relay coils' resistance. That is mostly to reduce the power dissipation in the coil so it's within the manufacturer's max-specified limit.
The other thing is that I found several burned-out #47 incandescent bulbs in the VU meters. They still are easy to find because they're used by the zillions in pinball machines! I found some drop-in LED replacements so the old beast should be good for another 30 years 😆.
I slide a thin metal scraper between the panel and the exciter foot, then twist the scraper gently to pry the foot off the panel. This usually doesn't harm the exciter or panel, except soft EPS or XPS panels may be marred slightly.
I have never had any need for solvents to remove the 3M adhesive from the exciter. Simply grab a loose bit and tug and it pulls right off.
To temporarily attach a "used" exciter (without the original adhesive) to a panel, I use a thin 3M double sided tape. I forget the number of my favorite 3M tape but will look when I'm back home. I cut a square of the tape about 1.5" x 1.5", and press it securely to the panel by kind of burnishing it with my fingers before removing the tape's release backer. Then I remove the backer and press the exciter firmly to the tape. This is usually strong enough to hold the exciter in place for more than long enough to do any listening tests or measurements without any additional support for the exciter. But if I forget and leave it overnight I may find it has fallen off in the morning. When done testing, I can easily remove the exciter with the scraper method above. I have a few exciters that have been re-used literally hundreds of time this way. Also, usually I can re-apply an exciter to the "used" tape, but usually I will "re-burnish" it to the panel using a scrap piece of the release film before re-applying the exciter. The same piece of tape and be re-used several times this way before it loses its tack and has to be replaced. It looks like I tried several exciter positions on the panel below, and left the tape behind just in case I wanted to try the same spot again!
Eric
Haha seems I wrote almost the identical post nearly two years ago, but with some suggestions for the tape:
These two work great: 3M 401M and 3M 9589. The other ones I suggested I have never actually tried but might work equally well.
Eric
These two work great: 3M 401M and 3M 9589. The other ones I suggested I have never actually tried but might work equally well.
Eric
A palate knife popped the exciter off pretty easily. It didn't even mar the XPS too much. The double-sticky on the ring came off in bits & pieces.
The butyl rubber tape I used to attach the panel to the frame took a bit more effort but that was because there was a lot more of it to remove. Next time I will evaluate the exciter/plywood combo before attaching it to the frame.
The butyl rubber tape I used to attach the panel to the frame took a bit more effort but that was because there was a lot more of it to remove. Next time I will evaluate the exciter/plywood combo before attaching it to the frame.
Hello Eucy,
Why no PVA on the plywood? For the aspect?
Our local DIY stores propose watered based wood finishing which are based on vinyl something...
On my current panels I used a polyurethane based varnish (because it is also quite standard...)
What is an Auto Acrylic clear coat?
Christian
Hello Mark
Good!
My experience is also to use some sharp blade to remove the exciter.
In the past, I used double side tape from the local DIY store but the performances were not excellent. So with double side tape, my advice would be to use one referenced in posts here.
I think to use any tape in a rectangular or square shape (I mean without removing the central area inside the voice coil diameter) can have an influence on the highest frequencies, at least for light materials like EPS. So for a "final" panel, if the exciter is glued, the FR might be different.
Currently, I use cheap PVA glue directly between the exciter and the panel. It is enough to keep in place the exciter and it has a good transmission of the HF. There is nearly no remaining glue on the exciter after... a bit now after between 5 to 10 uses of the same exciter. It can be removed with a blade avoiding any piece of dry glue in the voice coil gap.
About the finishing, my experience is limited. For my plywood panels, I used a thinned varnish. The idea was to try to have damping with low weight... Well, my last measurements didn't really show (or not that visible) a difference with a raw plywood. As I applied the varnished on only one side, I got a warped panel. This was my main problem. Hopefully, when it was glued on the peripheral suspension, it was flat. It is still in place after more than 2 years (by the way, the exciter with its original double side tape also). It is a 3mm plywood.
Christian
Christian
No PVA on plywood because:
1/ it will cause warping
2/ it raises the grain
3/ it's heavy unless well watered down and hence 1/ and 2/ problems again
4/ it is not easy to sand smooth.. Trends to be "chewy"
5/ it deadens too much
All imo of course
Spirit based shellac and acrylic lacquer based coatings are a lighter touch, dry harder can be easily standard, and esp with lacquer, don't cause warping to the extent of PVA
The term 'acrylic' when used with 'lacquer' can be confusing to people
This link will help explain it : https://vermontwoodsstudios.com/pages/lacquer#:~:text=Acrylic Lacquer,yellowing problems associated nitrocellulose lacquers.
Here is a typical clear coat in a rattle can
An advantage of this material is that it can be used to seal the timber before applying shellac, thereby limiting the penetration of the shellac coat
Eucy
No PVA on plywood because:
1/ it will cause warping
2/ it raises the grain
3/ it's heavy unless well watered down and hence 1/ and 2/ problems again
4/ it is not easy to sand smooth.. Trends to be "chewy"
5/ it deadens too much
All imo of course
Spirit based shellac and acrylic lacquer based coatings are a lighter touch, dry harder can be easily standard, and esp with lacquer, don't cause warping to the extent of PVA
The term 'acrylic' when used with 'lacquer' can be confusing to people
This link will help explain it : https://vermontwoodsstudios.com/pages/lacquer#:~:text=Acrylic Lacquer,yellowing problems associated nitrocellulose lacquers.
Here is a typical clear coat in a rattle can
An advantage of this material is that it can be used to seal the timber before applying shellac, thereby limiting the penetration of the shellac coat
Eucy
FYI, my product research for "clear coat" found that some products are water-based. Best to read the label before purchasing/using. Products whose name includes "enamel" or "lacquer" appear to be more likely to be solvent-based.
Christian,
How long does your PVA take to harden sufficiently to make a test? I don't have much patience when I'm testing. With the tape you can test immediately.
Eric
Dave,
My FEA program uses a thick plate model, so I decided to use it to see how much error the "thin plate model" might be introducing in your simulation, and in particular the determination of the panel's coincidence frequency. My conclusion (from the analysis below) is that it really doesn't introduce too much error for typical isotropic materials. Hopefully the analysis is sound! (pun intended).
I suspect you know the following, but am including it for context. Thin plate theory ignores shear deformation and rotary inertia, which is a good approximation as long as the plate is thin relative to its length. Typically panels have a length to thickness ratio of around 100 or more, so thin plate theory should apply. But at high frequencies, the real "characteristic length" isn't the length of the panel , but rather the length of the bending wave. And at high frequencies, the bending wavelength is much smaller than the length of the panel. So at sufficiently high frequencies, there is a point where the thin plate model is no longer a good approximation. Where does thin plate theory break down, I wondered, relative to the coincidence frequency? That's the question I wanted to answer.
The basic idea was to compare the bending wave speed predicted by the FEA model to the bending wave speed expected from the thin plate model, and determine at which conditions there is significant deviation.
From the equation for coincidence frequency using the thin plate model, I re-arranged it and came up with a parameter I named the "thin plate index" which represents the ratio of the bending wavelength at coincidence (per thin plate theory) to the panel thickness. As shown below, this "index" is a function of the panel's elastic properties, density, and the speed of sound (c).
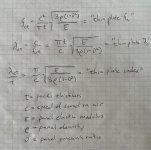
Then, I used my FEA program to model a simply supported beam for a wide range of values of the "index". For each different value of the "index", I computed the coincidence wavelength (per thin plate theory), and used that as the length of the beam. I then used the FEA modal vibration analysis to determine the resonant frequency of the second mode (which includes exactly one full wavelength). Finally, I calculated the bending wave speed by multiplying the beam length by the FEA calculated modal frequency. The results are shown in the plot below. The vertical axis is the ratio of the calculated bending wave speed to the speed of sound. The horizontal axis is the "thin plate index" described above.
Of course, since the coincidence frequency is defined as the frequency at which the bending wavespeed equals the speed of sound, the plot "should" be a flat horizontal line at 1.0. And that is exactly what happens for high values of the thin plate index. But at low values of the index (essentially low values of E/rho), the bending wavespeed is actually slower than the speed of sound. The implication (I believe) is that for plates with a sufficiently low value of "index", the coincidence frequency predicted by thin plate theory will be lower than the true coincidence frequency. From the plot, it looks like thin plate theory is very good for an index over 20, decent between 5 and 20, and going bad rapidly for an index of 5 or less.
I calculated the "index" for a couple of common materials, and came up with the results below.
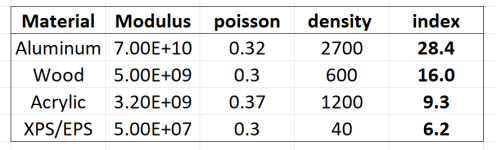
I think these cover the range of for most typical materials. Only for the PS foams does the index get low enough that the thin plate theory becomes questionable, and even then the error looks only to be on the order of 10% near coincidence, so not so bad after all.
Any thoughts (corrections?) would be appreciated.
Eric
Hello Eric,
Good question... It needs a certain time ;-). All kidding aside, it is not as fast as to use a tape. Steve already posted to say if I remember well that the sound can change over several days. For my test I generally glue an exciter one day to test it the day after.
Christian
Hello Eric,
I agree on the formula of what you call the index but I get lost with the sentence above.
The index is dimensionless (index = lambda_fc / h) so to get a beam length equal to the wave length of the coincidence frequency from the thin plate theory, you need to choose a thickness no?
In addition what I don't see (understand it is "does all of that remain physical in the idea of representative of our plate enough?". Our materials have a coincidence frequency from 5k (ie XPS 20mm) to more than 20kHz (acrylic or wood in 2mm) so a wave length in the air in the range let say 20mm (acrylic or wood 2mm) to 70mm (XPS 20mm). Considering their index from 6 for XPS to 10 and above for the other, it comes an XPS beam thickness of about 10mm and less than 2mm for the others which is not too far from the real thickness.
From FEA point of view is it correct to make a calculation on a beam with a ratio length to thickness going as low as 6?
Christian
Yes, to run the model, I needed to choose a thickness. But what thickness I chose shouldn't affect the plot. That is, if I chose a thicker plate, the corresponding wavelength would increase exactly in proportion, and the bending wave speed would be the same regardless of the panel thickness.
It depends on what exactly you mean by a "beam". That is to say, if by "beam" model of a plate, you mean a model based on thin plate theory, then no, it would not be correct. But when I said I modeled a "beam", what I meant is that I used a plate with a very small transverse dimension compared to it's length. That way the LISA FEA model ran a lot faster. But the plate model I used is not a "beam" (i.e. Bournoulli-Euler) model, but rather a Mindlin plate model, which should be valid even when the "beam" length is very short.
Eric
This is very cool. I think you should present this at an acoustics conference, but maybe that's more my thing than anybody else's in this forum!
I think I share the same general concern as Christian - I see how the thickness of the plate is normalized out because it's included in the "thin plate index," but is the beam length also unimportant in the results shown in that graph?
Christian,
Below is the data generated to create the plot. The column " f at Lct" is the determination from the FEA of the natural frequency at the thin plate coincidence wavelength. LInes 1 to 10 were the original data used in the plot. I used a thickness of 3 mm for all those lines. I modified the index (labelled below as "Lct/h") only by varying the modulus, but presumably I could have used any combination of E, rho, and density to obtain various values of the index, but since it is dimensionless, it should not matter how I got to any particular index value.
For line zero, to confirm my earlier answer to your question, I doubled the thickness to 6 mm. By doubling the thickness, the "coincidence" wavelength doubles, and the corresponding frequency doubles. And in the end, the ratio of the bending wave speed (Cb) to C remains the same.
Eric
I'm partway into getting my birch plywood panel ready for testing. The photo below shows it with one side that's been stained using Varathane honey oak, along with a roll of 3M 401 double-sided tape and a roll of painters tape. I still need to apply the lacquer I got. That won't happen until tomorrow because the stain needs to dry. I probably will bring it up from the basement -- it's on the chilly side down there, ~60F right now.
The panel is 24" x 24" x .25". Lowes also has 24 x 48 in stock if I want to try that.
The panel is 24" x 24" x .25". Lowes also has 24 x 48 in stock if I want to try that.
Christian,
I should have said that the frequency is cut in half, rather than doubles.
Eric