Amen. Somehow FIR filtering has become perceived as a panacea, a cure-all for every audio ailment. 'Taint so.
That said, IIR filtering also requires some "occult" knowledge. Limit cycles, coefficient sensitivities, and stability, in particular, can be big problems.
I have an unfounded suspicion that by expanding the capabilities of IIR, merging it with FIR, you are thereby introducing the disadvantage of FIR into IIR, as doctors say, we treat one thing, but cripple another. It is quite possible that such an approach will be interesting to someone from the theoretical side, this is quite good and justified, since a good theorist will quickly show the advantages and disadvantages of such an approach for the implementation of certain practical tasks, it is quite possible that there is some practical task in which such an approach will be justified. But off the top of my head, I personally do not see the advantages of this approach from a practical point of view, compared to the phase correction capabilities of classical FIR. I can be very wrong, since I am illiterate in theory.
Thanks for the link to the paper, @CharlieLaub. Skimming through it, the algorithm looks nice and simple, and computationally efficient as well.
Applying a minimum phase filter forward and then backward to get a linear/zero phase result is an old, well-known technique. It can be done in real time by truncating the IIR, reversing it in time, and then applying it using your favorite continuous convolution algorithm. I've been doing exactly this for years to correct the phase rotation from IIR crossovers (not sure it actually makes an audible difference; I do it just in case, I suppose).
Applying a minimum phase filter forward and then backward to get a linear/zero phase result is an old, well-known technique. It can be done in real time by truncating the IIR, reversing it in time, and then applying it using your favorite continuous convolution algorithm. I've been doing exactly this for years to correct the phase rotation from IIR crossovers (not sure it actually makes an audible difference; I do it just in case, I suppose).
Continuous FFT convolution algorithms are well established and produce no artifacts if done correctly. The result is identical to continuous direct convolution in the time domain, save for any round-off error due to finite numerical precision (which, for long filters, is larger with direct convolution).
One can get the same latency as the technique described in the paper via other methods, though it does seem that this new method is more computationally efficient:
- Direct convolution is not block-based and has zero latency (meaning you get a sample out for every sample you put in; the only latency is from the filter itself), but is very slow for long filters.
- Uniform partitioned FFT convolution gives latency equal to the partition size, but small partitions are slow. A non-uniform partitioning scheme (for example: 32, 64, 128, 256...) is more computationally efficient and has a latency equal to the smallest partition.
- Combining direct convolution and non-uniform partitioned FFT convolution results in zero latency and is reasonably efficient. The first partition is direct and the rest are FFT, with the smallest FFT partition set to the same length as the direct partition.
Truncating an IIR all pass filter causes ripple in the magnitude response, as shown by @KSTR in post #26.
@bmc0 Thanks for your thoughts.
On that last point, that is true for an FIR filter for sure. I have encountered that when I was playing around with FIR group delay EQ with short kernels a few years back. But I do not think that happens with this method, at least from what I have seen so far. It's something I need to take a closer look at.
On that last point, that is true for an FIR filter for sure. I have encountered that when I was playing around with FIR group delay EQ with short kernels a few years back. But I do not think that happens with this method, at least from what I have seen so far. It's something I need to take a closer look at.
Unless my understanding is incorrect, it must behave the same way. Fundamentally, the method truncates an IIR filter to produce an FIR filter, which is then time-reversed and applied to the input signal. The clever bit is this: the author figured out that the truncated filter and its time-reversed counterpart can be realized with cascaded sparse FIR filters having only two non-zero coefficients each. This is important because it allows efficient direct convolution regardless of the total filter length—one only has to compute the contribution of the two non-zero coefficients in each stage.
In your other comments, you seem to be conflating FFT convolution with FIR filtering/convolution in general. Frequency-domain convolution using FFT/IFFT is a common way to do convolution, but it isn't the only way. As I said above, the algorithm presented does direct (time-domain) convolution with sparse FIR filters.
This isn't an optimal solution in terms of latency, but for the general case you could just correct each crossover individually. LR and odd-order Butterworth crossovers are easy and can be corrected exactly since the sum is all pass (i.e. perfectly flat magnitude). For crossover topologies which don't have an all pass sum, approximate corrections such as the one shown in post #19 can be used.
Here are a few equivalent all pass representations, written as cascaded 1st (ap1) and 2nd (ap2(Q)) order sections:
- LR2: ap1
- BW3: ap2(1)
- LR4: ap2(sqrt(0.5))
- BW5: ap2(2/(1+sqrt(5)))
- LR6: ap1; ap2(1)
- LR8: ap2(1/sqrt(2+sqrt(2))); ap2(1/sqrt(2-sqrt(2)))
@bmc0 Thanks for those insightful posts with clear and concise info. Much appreciated.
One use of any group delay EQ method can be to take a system with problematic group delay (e.g. too high at low frequencies, or with excessive peaking) and bring that down "a bit" until the group delay is just below the audibility threshold. In my mind I see a system with IIR based crossovers that then has a band-aid applied with one or two reverse allpass filters. This approach is the same as what I mentioned earlier, to take steep, high group delay filters and make them "usable". Since I have recently been working on steep IIR filters this capability is definitely one that I will explore in the near future.
One use of any group delay EQ method can be to take a system with problematic group delay (e.g. too high at low frequencies, or with excessive peaking) and bring that down "a bit" until the group delay is just below the audibility threshold. In my mind I see a system with IIR based crossovers that then has a band-aid applied with one or two reverse allpass filters. This approach is the same as what I mentioned earlier, to take steep, high group delay filters and make them "usable". Since I have recently been working on steep IIR filters this capability is definitely one that I will explore in the near future.
Below is an example of how I think the reverse-IIR processing can improve group delay problems with any crossover.
I recently released a family of steep IIR crossovers with controlled group delay, published in the September issue of AudioXpress. The DFE crossover filters are derived from ellliptic filters and then optimized to reduce group delay and to make the HP+LP sum as flat as possible. The steepness of these sorts of crossover filters is limited by increasing group delay that occurs due to one or more relatively high Q poles located near the passband edge. These can produce significant group delay peaking around Fc. But if I could EQ away this GD peaking, I could design much steeper filters.
To provide an example I developed a 10th order DFE type crossover having a 1kHz crossover frequency. It's a "squared" crossover, that is two identical 5th order filters in series. The magnitude response is down more than 50dB at only 1.15 * Fc (1.2 octaves). This sort of steepness is typically only seen from FIR filters because any IIR or analog active version would result in the group delay shown. Here is what this crossover looks like:
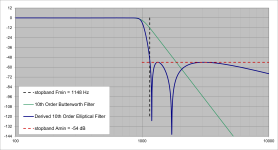
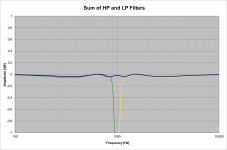
The HP filter is the LP reflected about Fc=1kHz. The "squared" form is useful for higher order DFE crossovers, and it also simplifies the group delay EQ via reverse-IIR filtering because you can use two RIIR allpass filters equal to the two second order sections in on of the 5th order "halves" of the filter. The problem with this filter is the group delay peaking - it far exceeds the audible threshold for this frequency range (1k Hz).
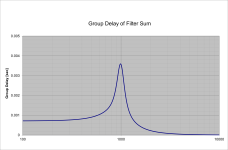
We can still use this filter if we use RIIR to EQ the group delay peak. We don't need to completely eliminate the group delay, just reduce it to innocuous and inaudible levels. I did a by-eye fit of the DFE Crossoer group delay using two 2nd order allpass filters. These reduce the group delay significantly, leaving only the orange curve in the plot, below, which is far below the limit of audibility and also very smooth vs frequency.
What I find attractive is that these steep IIR filters remain computationally efficient even at low frequencies. Likewise, the reverse-IIR filters are also efficient despite adding latency. So together these represent new possiblities with IIR based, steep crossovers. Interesting to me, at least!
I recently released a family of steep IIR crossovers with controlled group delay, published in the September issue of AudioXpress. The DFE crossover filters are derived from ellliptic filters and then optimized to reduce group delay and to make the HP+LP sum as flat as possible. The steepness of these sorts of crossover filters is limited by increasing group delay that occurs due to one or more relatively high Q poles located near the passband edge. These can produce significant group delay peaking around Fc. But if I could EQ away this GD peaking, I could design much steeper filters.
To provide an example I developed a 10th order DFE type crossover having a 1kHz crossover frequency. It's a "squared" crossover, that is two identical 5th order filters in series. The magnitude response is down more than 50dB at only 1.15 * Fc (1.2 octaves). This sort of steepness is typically only seen from FIR filters because any IIR or analog active version would result in the group delay shown. Here is what this crossover looks like:
The HP filter is the LP reflected about Fc=1kHz. The "squared" form is useful for higher order DFE crossovers, and it also simplifies the group delay EQ via reverse-IIR filtering because you can use two RIIR allpass filters equal to the two second order sections in on of the 5th order "halves" of the filter. The problem with this filter is the group delay peaking - it far exceeds the audible threshold for this frequency range (1k Hz).
We can still use this filter if we use RIIR to EQ the group delay peak. We don't need to completely eliminate the group delay, just reduce it to innocuous and inaudible levels. I did a by-eye fit of the DFE Crossoer group delay using two 2nd order allpass filters. These reduce the group delay significantly, leaving only the orange curve in the plot, below, which is far below the limit of audibility and also very smooth vs frequency.
What I find attractive is that these steep IIR filters remain computationally efficient even at low frequencies. Likewise, the reverse-IIR filters are also efficient despite adding latency. So together these represent new possiblities with IIR based, steep crossovers. Interesting to me, at least!
Elliptic filters (or steep transition-band filters in general) not only have undesirable group delay; they also have long-duration impulse responses. Linearizing the group delay does not reduce the duration of the impulse response. How long is too long? I don't know.
@gberchin
OK. So this is the same phenomenon that happens with steep FIR filters (even if phase linear), where in there is ringing for each of the highpass and lowpass filters that make up the crossovers but if you combine them "perfectly" (e.g. on axis for a loudspeaker) the ringing from each cancels out and the impulse of the resulting sum is very clean? But then when you move off axis and the cancellation is no longer successful, the summed response also has ringing? At least that I what I recall was one issue with steep FIR filters...
OK. So this is the same phenomenon that happens with steep FIR filters (even if phase linear), where in there is ringing for each of the highpass and lowpass filters that make up the crossovers but if you combine them "perfectly" (e.g. on axis for a loudspeaker) the ringing from each cancels out and the impulse of the resulting sum is very clean? But then when you move off axis and the cancellation is no longer successful, the summed response also has ringing? At least that I what I recall was one issue with steep FIR filters...
Yes. Filtering is filtering. Whether FIR or IIR, digital or analog, is merely a detail of implementation.
Since I can't edit my post: I worded this in a misleading way. Just to clarify, the electrical summed response of LR and odd-order BW crossovers can be represented exactly with IIR all pass filters. The time-reversed phase correction filter must of course be truncated for practical application to an indefinite length signal. So, more accurately, the correction can be arbitrarily close to exact depending on acceptable latency.
My setup has two IIR crossovers: 5th-order Butterworth at 85Hz and 6th-order Linkwitz-Riley at 1.05kHz (acoustic slopes, not electrical). The phase correction filter is 2048 taps at 44.1kHz (~46ms) and has a maximum peak-to-peak ripple of less than 2.5×10^-7 dB. A shorter 1024-tap filter has a maximum peak-to-peak ripple of about 0.004dB, which is certainly still acceptable. Latency isn't particularly important in my setup, so I use the longer filter just because 🙂.
Looks like an interesting application of the technique. As others have pointed out, it's true that one could get the same result (including latency) with a conventional FIR technique, but I think this new method is probably more computationally efficient (though somewhat less flexible).
I don't know what the threshold might be regarding ringing when the high pass and low pass sections don't line up in time (i.e. off axis vertically for a speaker with vertically-aligned drivers). Any steep linear or near-linear phase filter will have notable pre-ringing. As @gberchin said, pure FIR vs IIR+correction doesn't make a difference in this respect. If the resulting magnitude and phase responses are identical, the impulse responses must also be identical.
Also horizontally when the tweeter and woofer polar responses don't match.
I don't know where the audibility threshold lies either.
However, I do feel confident that steep linear phase xovers can be successfully used without any audible pre-ring.
The key is of course maintaining acoustic complementary summation both on and off axis.
I've found steep helps do this much more so than shallow. By a large factor.
Regarding the audibility threshold and ringing - many of the investigations about group delay audibility that one can find in the academic literature use something like a single impulse to determine the threshold. In this case, there is the impulse but away from that in time there is nothing, and so pre- and post- impulse tails/ringing will stand out more. With continuous music signals you have masking. Evidently this masking after the main peak is stronger than before. So the audibility threshold will depend on the signal itself to some extent do to the variability of masking within it.
So far I have been focused on how to reduce group delay produced by the crossover sum. In addition to that, it might be interesting to look at the response from each crossover alone, e.g. the LP impulse response, and the HP impulse response, to gain a better understand of the ringing of each (based on recent comments here, these will still ring). This would shine some light on the "off-axis ringing" issue, I think, and it would not be too difficult to do.
So far I have been focused on how to reduce group delay produced by the crossover sum. In addition to that, it might be interesting to look at the response from each crossover alone, e.g. the LP impulse response, and the HP impulse response, to gain a better understand of the ringing of each (based on recent comments here, these will still ring). This would shine some light on the "off-axis ringing" issue, I think, and it would not be too difficult to do.
@CharlieLaub and @bmc0 , thank you both (as well as others) for the value input. I'm busy the next weeks with my day job and touring with the band on weekends but later on I will try to get my own demo code running as that is the usual way for me to really understand a new algorithm. And this one is extremely tempting, phase compensation (or general XO) at low frequencies at high sample rates has always been a challenge with FIR as well as with IIR. Many people use/used lower sample rates like 1/2 to 1/8 for that but it's not feasible for global phase correction.
It is actually possible to clarify even further: LR crossovers are just a special case of in-phase allpass crossovers That means there are some additional crossover functions that could be exaclty corrected with the method presented here by using "inverse allpasses". OTOH they are asymmetrical and less steep than LR. Most probably they are therefore not too interesting for the application of this correction method. But for people who don't intend tho use any DSP at all they could be interesting because they allow very flat group delay curves like the orange one in post #48 from the start. But this would come at the cost of much less steep high- and lowpass slopes.
Regards
Charles
P.S. A technically more correct thread title would have been: "Removing Loudspeaker Group Delay Distortion by using reverse-IIR filtering".
Yes, the title gives the impression that it is somehow possible to invert the phase characteristic and thereby remove the group delay of an IIR filter.
Yes, although I'd guess that in general the additional forward (post) masking would be more significant than backward (pre) masking. Most music signals largely consist of impulsive onsets with slower decay.
Thinking about it more, I'd be inclined to doubt that pre-ringing from linear/near-linear phase crossovers is much of an issue in practice. In the case of pre-ringing in the direct sound, the spectral coloration from poor summation would probably be more objectionable than the ringing itself (save for extreme cases, perhaps). Pre-ringing in the reflected sound would be masked by the first arrival unless the ringing is substantially longer duration than the reflection delay.
THAT is exactly what it does, yes. You can do this for a filter, or an entire loudspeaker.