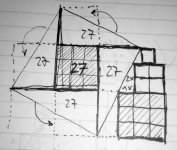
Google knows. A sort of lion's claws, and not all agree what it actually meant.That sounded like Greek to me ... 😉
66.843
Monsieur, with all respect, your solution appears to be IRRATIONAL.... 😕
Could very well be, the puzzle is not fully defined, so I made some guesses.Monsieur, with all respect, your solution appears to be IRRATIONAL.... 😕
@ mchambin The numbers represent the areas of the squares.
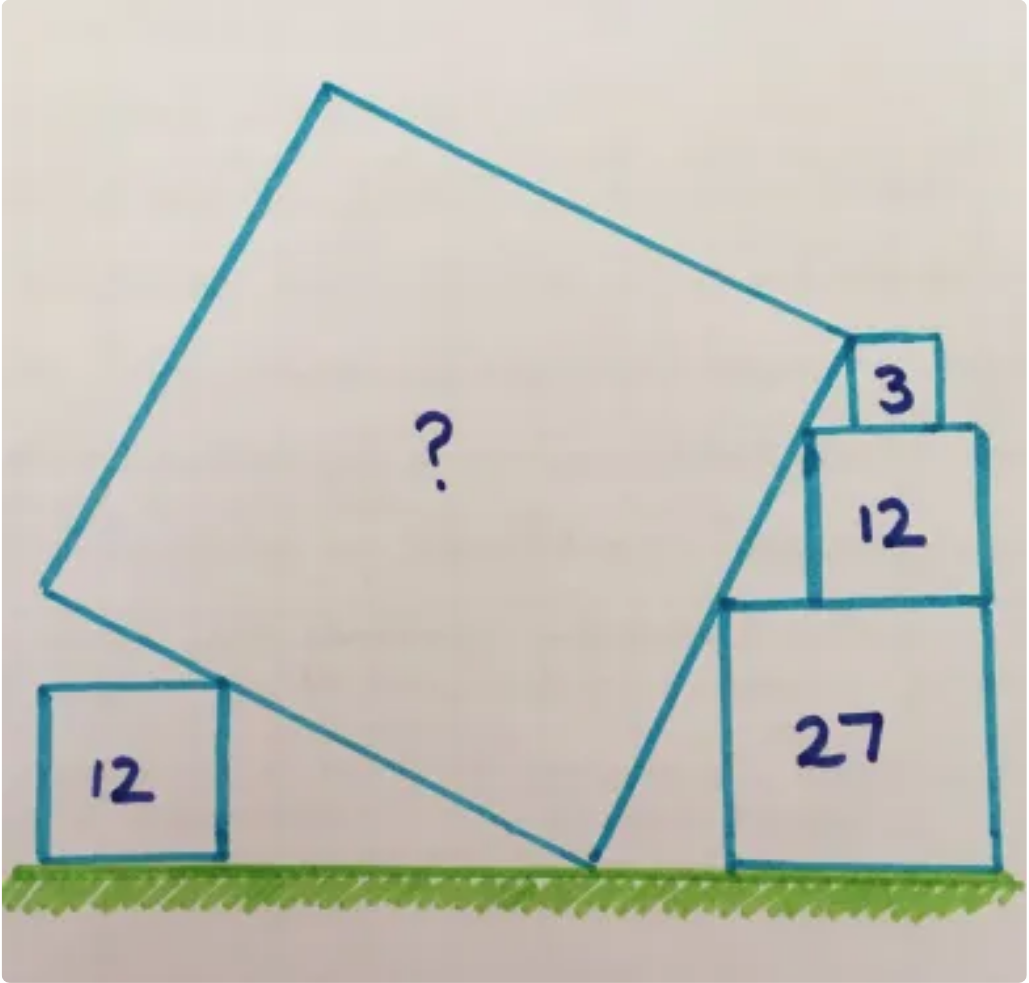
So the vertical height of the right hand corner of the big square is given by x + y + z where x, y and z are the heights of each block in the right hand stack.
So, 3 = x^2, 12 = y^2 and 27 = z^2
Hence x = √3, y = 2√3 and z = 3√3
So, the total vertical height is 6√3
6√3 is also the horizontal length of the triangle formed by the sloping base of the big square which contains the single area 12 square.
Nearly there! 😀
So the vertical height of the right hand corner of the big square is given by x + y + z where x, y and z are the heights of each block in the right hand stack.
So, 3 = x^2, 12 = y^2 and 27 = z^2
Hence x = √3, y = 2√3 and z = 3√3
So, the total vertical height is 6√3
6√3 is also the horizontal length of the triangle formed by the sloping base of the big square which contains the single area 12 square.
Nearly there! 😀
Last edited:
Are they, all squares?
The figures give the edge size ?
Ok, I got it.
Indeed, they are squares.
The number inside is not the size of the square.
😎Hence x = √3, y = 2√3 and z = 3√3
Nearly there! 😀
Last edited:
Subtract the length (2√3) of the single 12 square from 6√3 and you're left with 4√3, which forms the adjacent side of a small triangle with opposite side 2√3.6√3 is also the horizontal length of the triangle formed by the sloping base of the big square which contains the single area 12 square.
The hypotenuse of that small triangle can then be calculated by taking the square root of [(4√3)^2 + (2√3)^2] which equals √60.
The secret throughout is not to get involved in calculating the actual value of the square roots (which only generates awkward numbers) as we are looking for relationships between the various lengths.
Hence √60 is best written as √(4x15) or 2√15.
Almost home! 😉
Galu,
I used a scaling factor sqrt(3).
Then got all integers, 1 2 3, for an easy drawing.
There are many similar triangles with right edges in a 1/2 ratio.
I used a scaling factor sqrt(3).
Then got all integers, 1 2 3, for an easy drawing.
There are many similar triangles with right edges in a 1/2 ratio.
Last edited:
The single area 12 square divides the base of the triangle formed by the sloping base of the big square into the ratio 2√3:4√3 or 1:2
The sloping base of the big square must also be divided in the ratio 1:2 by the right hand apex of the small area 12 square.
The '2' part of the ratio is 2√15 so the '1' part must be √15.
We now know the side of the big sloping square has length 3√15 giving its area as (3√15)^2 = 135.
The proof of Steve's answer is now complete. 😎
The sloping base of the big square must also be divided in the ratio 1:2 by the right hand apex of the small area 12 square.
The '2' part of the ratio is 2√15 so the '1' part must be √15.
We now know the side of the big sloping square has length 3√15 giving its area as (3√15)^2 = 135.
The proof of Steve's answer is now complete. 😎
I did it much more simply. Not a trace of Mathematical Rigour here. I was running on Instinct. I felt it was important to kick my friend Monsieur mcchambin into his rightful place with the fastest solution! Desperate times call for desperate measures.
I just used my eyes and noticed the answer exceeded the square of area 27 by above a factor of 4. I have also picked out that Mr. Cal Weldon has an obsession with 2x1 triangles and squares. Which, as we know, involve the square of the sine of the smallest angle, 1/5.
The rest, as they say, is just technique. The answer was 5x27= 135. How hard was that? 🙂
I just used my eyes and noticed the answer exceeded the square of area 27 by above a factor of 4. I have also picked out that Mr. Cal Weldon has an obsession with 2x1 triangles and squares. Which, as we know, involve the square of the sine of the smallest angle, 1/5.
The rest, as they say, is just technique. The answer was 5x27= 135. How hard was that? 🙂
how hard was that? 🙂
Not sure ...
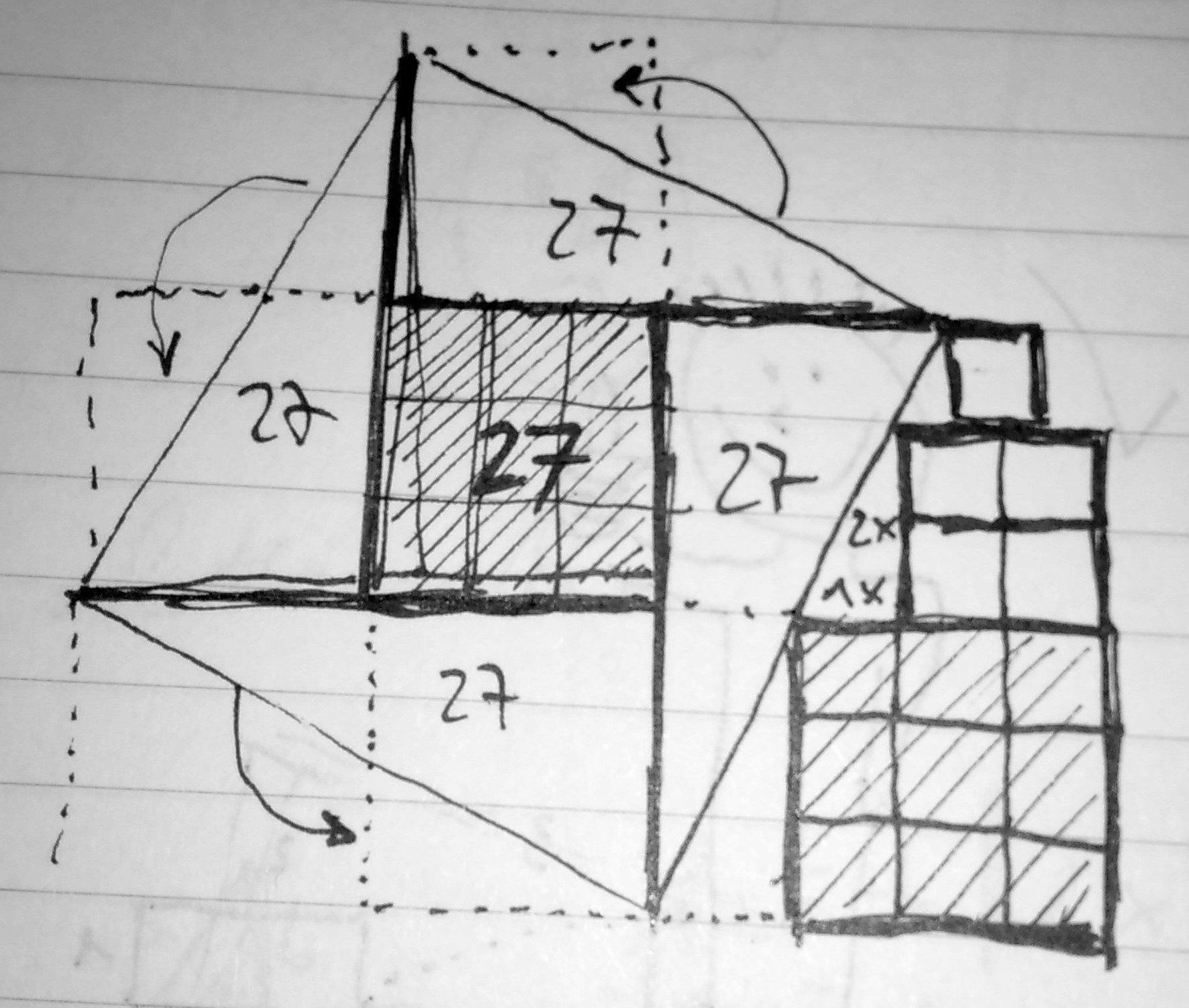
Is this just another explanation as shown in my sketch?
Attachments
But that is just a sketch, not an explanation.Not sure ...
Is this just another explanation as shown in my sketch?
Can you explain the solution in words?
Triangle next to squares has a height of 2 x "27" square, if you refer to the the subdivision squares (surface 3 each).
Triangles inside big square are all equal.
Triangles have ratio 2/1, so they must also have surface of 27.
In the center remains a square with 27.
Total 5 x 27
Triangles inside big square are all equal.
Triangles have ratio 2/1, so they must also have surface of 27.
In the center remains a square with 27.
Total 5 x 27
I replaced my post!
I understand your first sentence, but could do with a tad more explanation after that.
So, the 12 square on the left is just a red herring!
I understand your first sentence, but could do with a tad more explanation after that.
So, the 12 square on the left is just a red herring!
The thing about these puzzles is that there are different ways to arrive at the answer.
The mathematicians who set them take great delight in seeing the variety of different solutions which are submitted.
The intuitive among us can instinctively find a direct way to the solution.
I'm not one of them!
The mathematicians who set them take great delight in seeing the variety of different solutions which are submitted.
The intuitive among us can instinctively find a direct way to the solution.
I'm not one of them!

I wish people wouldn't post unnecessarily large images. It's bad for the planet, you know. And requires more storage by diyaudio, which costs them money.
I think a lot of time can be saved on these puzzles by stripping out what is misleading and seeing what is important.
I was looking for a visual proof of the proposition, and stv seems to have found one:
I do prefer geometric demonstrations to algebraic ones, being a visual person rather than abstract.
I was wondering if the nice way to do this would be to normalise the problem to roots of unity, and one of my tasks today might be that:
Quanta Magazine
I also noticed the three squares on the right are in a ratio of 1:4:9 which suggests other elegant avenues.
I also noticed, on editing, this complex post is a giant acronym of i. The root of -1. 😱
I think a lot of time can be saved on these puzzles by stripping out what is misleading and seeing what is important.
I was looking for a visual proof of the proposition, and stv seems to have found one:
I do prefer geometric demonstrations to algebraic ones, being a visual person rather than abstract.
I was wondering if the nice way to do this would be to normalise the problem to roots of unity, and one of my tasks today might be that:
Quanta Magazine
I also noticed the three squares on the right are in a ratio of 1:4:9 which suggests other elegant avenues.
I also noticed, on editing, this complex post is a giant acronym of i. The root of -1. 😱
Last edited:
- Home
- Member Areas
- The Lounge
- Something to lighten the mood