I went to the doctor yesterday, and he diagnosed me with paranoia... well, he didn't actually say it.. but I could tell.
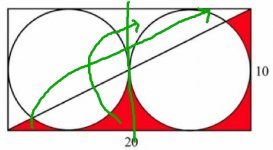
Roughly you can say the the area outside the circles are:
TOTAL AREA = 10*20 - 2*(π*5^2) = 200 - π*50; with π*5^2 being the area of one circle.
The diagonal line divides this area in two:
AREA = 100 - π*25 = 25*(4-π)
Or you can simple move areas around due to the high degree of symmetry and calculate area this way:
AREA = 10*10 - π*5^2 = 25*(4-π)
TOTAL AREA = 10*20 - 2*(π*5^2) = 200 - π*50; with π*5^2 being the area of one circle.
The diagonal line divides this area in two:
AREA = 100 - π*25 = 25*(4-π)
Or you can simple move areas around due to the high degree of symmetry and calculate area this way:
AREA = 10*10 - π*5^2 = 25*(4-π)
Attachments
I ruined everything, didn't I ....
you didn't.
see "part two" in cal weldon's post 1122: https://www.diyaudio.com/forums/the-lounge/351277-lighten-mood-113.html#post6815208
Last edited:
I have had to go down the same segment road, stv, and I don't like it.... 😀
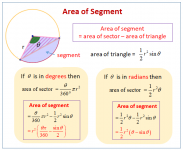
Circular segment - Wikipedia
Segment A / Circle Area = (x - sin x) / 2 Pi... where x is the angle subtended by the segment as seen from the centre of the circle. The solution is apparently irrational and transcendental in general.
The diagonal angle is horrible... 26.56505118... degrees. 0.463647609... in radians. But expressable as trig functions of roots.
Have reduced the problem to sines and Pi now. I am hoping some stuff will cancel out and I get some sort of neat algebraic solution for this particular 2 by 1 rectangle. Might be some ratios of square roots. Nearly there! I hope. 😕
Circular segment - Wikipedia
Segment A / Circle Area = (x - sin x) / 2 Pi... where x is the angle subtended by the segment as seen from the centre of the circle. The solution is apparently irrational and transcendental in general.
The diagonal angle is horrible... 26.56505118... degrees. 0.463647609... in radians. But expressable as trig functions of roots.
Have reduced the problem to sines and Pi now. I am hoping some stuff will cancel out and I get some sort of neat algebraic solution for this particular 2 by 1 rectangle. Might be some ratios of square roots. Nearly there! I hope. 😕
Attachments
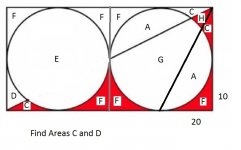
We need to know the area of the segment of the circle contained within the small right angled triangle at bottom left of Allen's diagram.
Area of small red bit = area of small right angled triangle - (area of circle segment + area of large red bit)
There is a formula for calculating the area of the circle segment to which I have previously given a link.
It will be now seen that the final solution hinges on the determination of the angle θ.
I don't know if this method satisfies the mathematical purists, but it works! 😎
Area of small red bit = area of small right angled triangle - (area of circle segment + area of large red bit)
There is a formula for calculating the area of the circle segment to which I have previously given a link.
It will be now seen that the final solution hinges on the determination of the angle θ.
I don't know if this method satisfies the mathematical purists, but it works! 😎
Attachments
When done, there's enough to knit a pair of socks.
The Mrs. always does that with his fur. She likes to freak me out with that 'ghost' thing.
Sigh, I love her anyway.
A coat for my brothers boxer ... it's my brother's brother sitting in the armchair btw and I am wondering if I want a crazy dog in my lap.
Thanks!
My brother is a boxer guy. This is Greta (Thunberg), his 4th or 5th boxer. Really coll dogs - the never seems to "grow up".
My brother is a boxer guy. This is Greta (Thunberg), his 4th or 5th boxer. Really coll dogs - the never seems to "grow up".
Magnus, I have Boxer friends. One of them calls each one 'Rocky'. Not sure if he's into the movie thing but I think he is up to Rocky 4 by now. Too bad they don't last so long as Boxers are really cool dogs as you say.