I see. I tried some random samples but it was always bad, much worse than without the sphere present - what approximate distances and radii had you in mind?Unfortunately I don't have that possibility and doubly unfortunate that I am not likely ever to have it. That's just not what I do these days.
Hmm, I don't know how to test that.What if the rollback were covered in foam too?
Last edited:
This could be useful:
Jörg Panzer has commented on simulating (the effect of) "stuffing" tapped horns with damping material :
"You can take into account losses by lowering the quality
factors as provided in the Enclosure and Duct components. However, the
correspondence between the effect of material and these quality factors is
not provided. Typically it is regarded as a difficult issue and in many
cases best controlled by your experience. The isothermal effect can be
taken into account by slightly increasing the volume of the component.
Theoretically the upper bound is 1.4.
Rule of thumb: Run the simulation with low losses in order to see
resonances clearly. Then play with the quality factors to learn about the
sensitivity of the response to these parameters."
Someone used multiple duct elements with a larger viscosity to approximate a waveguide.
The standard viscosity is 1. When using a larger number you increase the viscosity.
By attaching tiny duct elements of a specific viscosity to the back of the mouth, you might be able to simulate foam.
Jörg Panzer has commented on simulating (the effect of) "stuffing" tapped horns with damping material :
"You can take into account losses by lowering the quality
factors as provided in the Enclosure and Duct components. However, the
correspondence between the effect of material and these quality factors is
not provided. Typically it is regarded as a difficult issue and in many
cases best controlled by your experience. The isothermal effect can be
taken into account by slightly increasing the volume of the component.
Theoretically the upper bound is 1.4.
Rule of thumb: Run the simulation with low losses in order to see
resonances clearly. Then play with the quality factors to learn about the
sensitivity of the response to these parameters."
Someone used multiple duct elements with a larger viscosity to approximate a waveguide.
The standard viscosity is 1. When using a larger number you increase the viscosity.
By attaching tiny duct elements of a specific viscosity to the back of the mouth, you might be able to simulate foam.
Last edited:
Nah, I don't think so. All I can do in this case is to set some absorption to some boundary elements.
Last edited:
mabat I'm wondering if you can help me to figure something out.
I have been trying the blended coverage equations together with the desmos examples you showed.
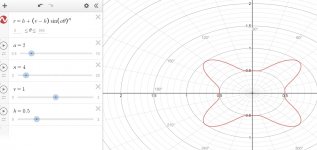
I tried to input this from desmos shot below in Ath as
Coverage.Angle = 45 - 22.5*sin(2*p)^4
This the raw shape that comes out

If I rotate it 45 degrees I get the shape I want Ath to morph to rectangular but that's the part I can't work out, is there a way?

I have been trying the blended coverage equations together with the desmos examples you showed.
I tried to input this from desmos shot below in Ath as
Coverage.Angle = 45 - 22.5*sin(2*p)^4
This the raw shape that comes out
If I rotate it 45 degrees I get the shape I want Ath to morph to rectangular but that's the part I can't work out, is there a way?
Attachments
Sure, just modify the formula: Graphing Calculator
You only have to set the angle value in radians, which in your case (45 deg) is π/4:
Coverage.Angle = 45 - 22.5*sin(2*(p - 0,7853981634))^4
You only have to set the angle value in radians, which in your case (45 deg) is π/4:
Coverage.Angle = 45 - 22.5*sin(2*(p - 0,7853981634))^4
Last edited:
Please change "," to "." in the formula, of course, otherwise it won't work.
BTW this is also the way how to set some feature only for e.g. 30 deg (and the respective symmetrical angles perhaps).
And you can then combine all this together - that's the beauty of the approach.
BTW this is also the way how to set some feature only for e.g. 30 deg (and the respective symmetrical angles perhaps).
And you can then combine all this together - that's the beauty of the approach.
A funny thing is that by introducing the parameter "k" I can leave out the special handling of a conical profile, into which the formula now naturally transforms for k=0: OS-SE Waveguide II
BTW, isn't the profile exponential for very high k values? 🙂
BTW, isn't the profile exponential for very high k values? 🙂
Sure, just modify the formula:
You only have to set the angle value in radians, which in your case (45 deg) is π/4
Thanks, that worked, I can see another rabbit hole of possibilities opening up 😉BTW this is also the way how to set some feature only for e.g. 30 deg (and the respective symmetrical angles perhaps).
And you can then combine all this together - that's the beauty of the approach.
Attachments
It does open up, the more if you realize that all the profile parameters can be changed independently around the axis this way.
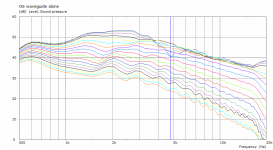
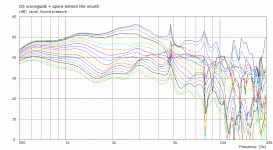
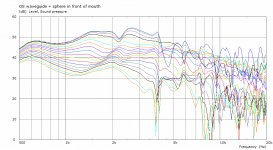
I see. I tried some random samples but it was always bad, much worse than without the sphere present - what approximate distances and radii had you in mind?
I am not surprised that it doesn't work. It was just an idea. But a sphere about the radius of a half wavelength of an axial hole in an OS place at about half wavelength from the mouth was what I had in mind. If you could post just this one test I'd be happy 🙂
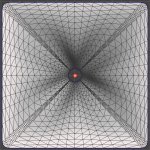
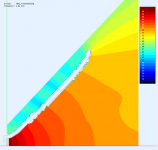
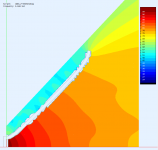
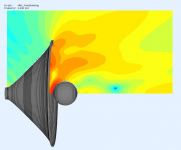
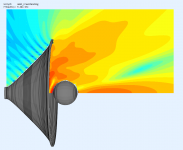
I wasn't sure what side of the mouth plane you meant so I made both. Axial hole at aprox 4.8 kHz (wasn't easy to get the hole back!), sphere radius 36 mm. Free standing waveguide ⌀320 x 140 mm.
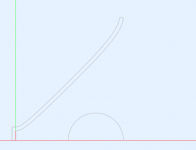
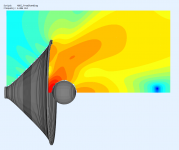
The experiment setup (sphere behind the mouth on this picture):

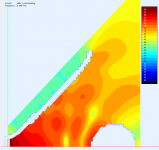
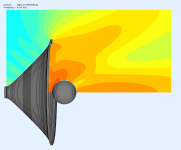
The WG alone:

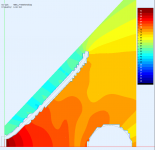
The sphere 36 mm behind the mouth (closer to the throat):

The sphere 36 mm in front of the mouth:

Do you want me to make some more? 🙂
The experiment setup (sphere behind the mouth on this picture):
The WG alone:
The sphere 36 mm behind the mouth (closer to the throat):
The sphere 36 mm in front of the mouth:
Do you want me to make some more? 🙂
Attachments
- Home
- Loudspeakers
- Multi-Way
- Acoustic Horn Design – The Easy Way (Ath4)