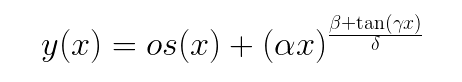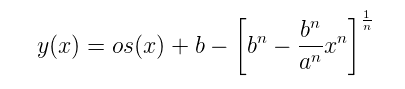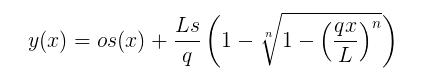A few pictures will tell more than a thousand words, I only have to code it first. Then I will show better what I mean.
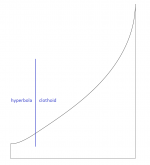
Actually it is easy to match both. The slope is allways matched by simply rotating the clothoid - it doesn't matter where it starts. Curvature increases linearly along its length so it's all about finding the right point.Don't the two curves have to match slope, not curvature? With slope only A works.
Attachments
Mabat,
In post 212, you show a poorly terminated os (your pic below).
Is that poorly terminated because of the last bend to the mouth (baffle) ?
If so, what would a good os look like ?
I though os was conical, but with a rounded throat, then a round over at the mouth.
Couldn't tell you how fast it opens, just better dispersion for a wider mouth to distance to throat.
How to Reduce Diffraction on Your Conical Horn
In post 212, you show a poorly terminated os (your pic below).
Is that poorly terminated because of the last bend to the mouth (baffle) ?
If so, what would a good os look like ?
I though os was conical, but with a rounded throat, then a round over at the mouth.
Couldn't tell you how fast it opens, just better dispersion for a wider mouth to distance to throat.
How to Reduce Diffraction on Your Conical Horn
Attachments
Last edited:
Yes, it's too small, too abrupt.Is that poorly terminated because of the last bend to the mouth (baffle) ?
OS is not a cone with a rounded throat. It's hyperbola from the throat to infinity. Mouth termination is not part of OS and should be as smooth/gradual as possible - at least this is obvious from the calculations so far. It's a continuum, there's no dividing line between right and wrong, however.
Closer still...
Not much of use I guess, but it's nice.
Not much of use I guess, but it's nice.
Attachments
Last edited:
Ahhhhhh, thank you.
That makes sense.
Many os ive seen seem to have that last soft corner (mouth break ?).
I'd figured it was a place that could be improved.
Tricky where to deviate from conical, and how fast to do it.
Even my 2384 has a bit of bend in the path before the last mouth round over.
I bet it helps (conical slight bending).
Again, thank you.
That makes sense.
Many os ive seen seem to have that last soft corner (mouth break ?).
I'd figured it was a place that could be improved.
Tricky where to deviate from conical, and how fast to do it.
Even my 2384 has a bit of bend in the path before the last mouth round over.
I bet it helps (conical slight bending).
Again, thank you.
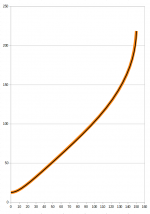
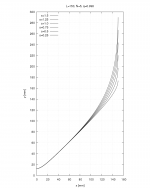
I've finally managed to figure out the one-describe-it-all equation, from throat to mouth.
Not there yet, but close... 🙂
(Black line is an OS connected to a clothoid, orange line is the new equation.)
That is exactly the kind of equation that I had in mind when I mentioned this before. Nice work.
Yep, I know, thanks. I only have no idea how to calculate all the parameters based on desired horn dimensions. Right now it's only fitted to a particular sample - just a quick excercise. I also felt there must be an equation like this, maybe this is not even the best one...
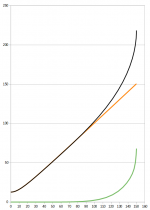
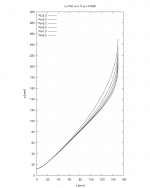
Oh, and it actually should go like this -
Oh, and it actually should go like this -
Attachments
Last edited:
Now that I think of it, it would have to be a two part equation. The first pure OS and then the OS plus equation, right? The joining point and the total length would set the values of the parameters.
The second term is almost zero near the throat - it makes no real difference and can be allways added, so one part equation like this is well possible.
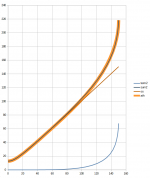
What I meant is to how to make the shape copy a clothoid, based on throat diameter, coverage angle and the length of the horn (which must be a parameter). It's not at all obvoius to me. Maybe someone could try...
(In the presented example clothoid begins at half of the length. This could be fixed or be a parameter as well.)
It may be that it is not really necessary to follow a clothoid, who knows...
What I meant is to how to make the shape copy a clothoid, based on throat diameter, coverage angle and the length of the horn (which must be a parameter). It's not at all obvoius to me. Maybe someone could try...
(In the presented example clothoid begins at half of the length. This could be fixed or be a parameter as well.)
It may be that it is not really necessary to follow a clothoid, who knows...
Last edited:
The green line also resembles a segment of a superellipse (n ~ 5). That would make another neat equation, maybe somewhat simpler to implement.
Superellipse - Wikipedia
Superellipse - Wikipedia
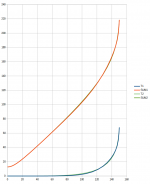
I really like the last equation, it gives tremendous design freedom and requires only a very simple and intuitive setting. This seems like the way to go. Who would have thought about that...
Attached is a sample spreadsheet.
Attached is a sample spreadsheet.
Attachments
Last edited:
- Home
- Loudspeakers
- Multi-Way
- Acoustic Horn Design – The Easy Way (Ath4)