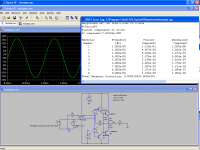
You probably missed the fact that the example was about slew-limiting with a 30kHz sinewave.
Here is the behavior with a 1kHz sinewave:
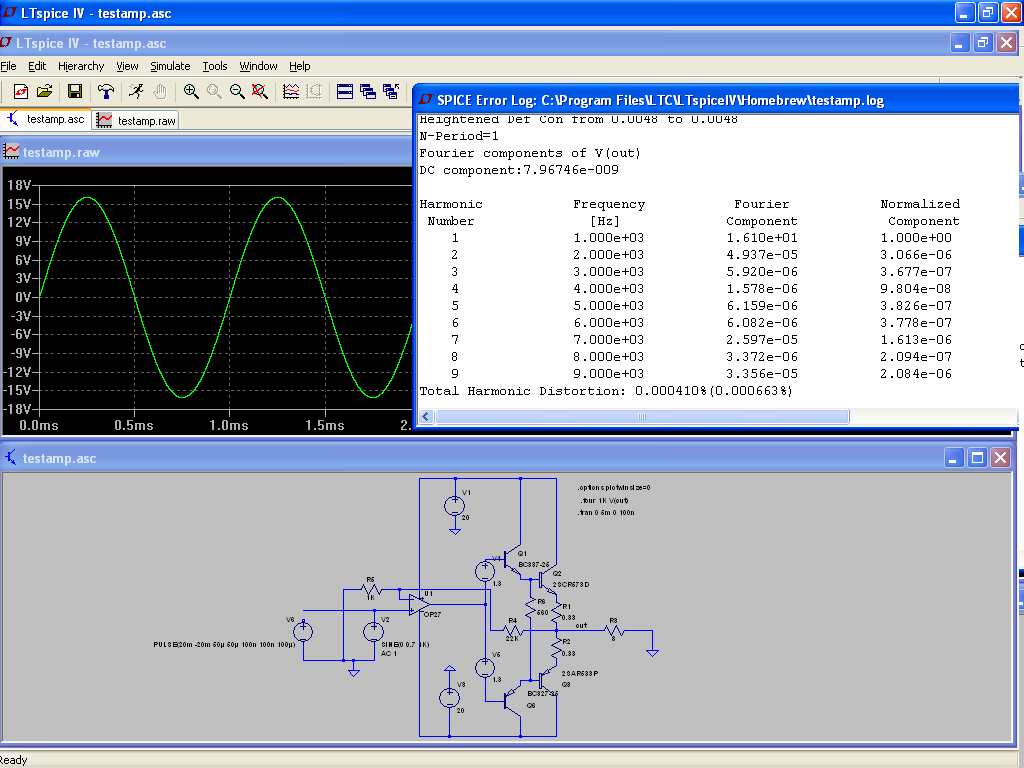
Note that I took the first opamp I stumbled on; with a type slower and having a higher loop gain, the effect would be even more striking, both for the THD and the slew limiting
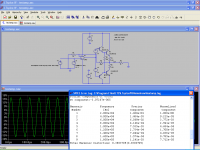
Here is the behavior with a 1kHz sinewave:
Note that I took the first opamp I stumbled on; with a type slower and having a higher loop gain, the effect would be even more striking, both for the THD and the slew limiting
Attachments
Elvee,
ok, then can you run this simulation to get a THD figure for a 20kHz signal with this circuit ?
ok, then can you run this simulation to get a THD figure for a 20kHz signal with this circuit ?
Elvee,
Many Thanks for going through this trouble.
Stating the obvious, it seems an amp sporting a very respectable THD figure @ 1kHz does not necessarily perform so well with THD @ 20kHz.
I think even with increasing loop gain and/or idle current the THD figure @ 20kHz will not improve much. If it were that easy, we would not have anything to discuss on the forum. 😀
To achieve a reasonably low THD figure @ 20kHz of lets say 0.002% there will have to be some complexity added to the circuit.
It is fair to conclude that .002% THD with a 6us rise time @ 1kHz is perhaps achievable, yet .002% THD with a 6us rise time @ 20kHz not so much ?
Many Thanks for going through this trouble.
Stating the obvious, it seems an amp sporting a very respectable THD figure @ 1kHz does not necessarily perform so well with THD @ 20kHz.
I think even with increasing loop gain and/or idle current the THD figure @ 20kHz will not improve much. If it were that easy, we would not have anything to discuss on the forum. 😀
To achieve a reasonably low THD figure @ 20kHz of lets say 0.002% there will have to be some complexity added to the circuit.
It is fair to conclude that .002% THD with a 6us rise time @ 1kHz is perhaps achievable, yet .002% THD with a 6us rise time @ 20kHz not so much ?
It is indeed obvious that performances will always degrade with frequency.
If the degradation is caused by a decrease in loop gain alone, the THD will typically increase by 6dB/octave.
However, when the slew-rate limit is attained, the THD will increase much more brutally, even if there is still enough loop gain to maintain a low THD.
It would be very pervert to deliberately design an amplifier that way, ie. with a high loop gain, and a very poor SR, but it can happen inadvertently, with some topologies.
The example I gave is minimally simple, it uses only a single opamp with a single pole compensation as a VAS, and it already shows a brutal increase in THD somewhere between 10 and 20kHz.
Experts like Marcel or Jcx could give much more elaborate examples using composites, but it would be a waste of time, of course.
In a real amplifier, there is more room for complex behaviors, and the SR is not directly coupled with the small signal bandwidth.
In fact, a slow rise time can be an advantage: if in the test circuit, we use a decent audio amp having no SR issues, reducing the bandwidth can be beneficial.
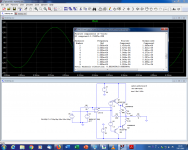
This is the THD of the circuit with its full bandwidth, 0.002%:
When a rolloff is deliberately introduced to increase the rise time to 6µs, the THD is almost halved, because the harmonics are subjected to more FB:
Attachments
Last edited:
Thanks again all. My curiosity is borne of the remarkably transparent sound of early British gear; bandwidth limited, FR rolled off, but typically fast rise/fall times. It's the Radford HD250 that caught my attention. I believe I did mistake the THD which should be .02 but still, it's an awfully slow amp to have garnered such high acclaim.
Be aware that rise/fall times (typically a small signal characteristic) and FR (also small signal) go hand in hand: you cannot have a rolled off FR and fast transition times.
There are also the large signal equivalents: slew-rate and power bandwidth, which also go together, but are mostly decoupled from the small signal characteristics, except that large signal performances can never surpass the small signal ones.
To make meaningful comparisons, you have to compare apples with apples: small signal with small signal, and large with large.
As I feebly attempted to show, the two groups can sometimes be heavily disconnected, with typically very good small signal performances and very poor large signal ones.
That said, if a gear has enough loop gain at HF to keep the THD low in the whole audio range, enough SR to reproduce it without added distortion, you may never notice that it is in fact rather limited according to objective, modern standards
Elvee,
Thanks for taking the time and your explanation. The simulation result with limited rise time to 6µs is quite the opposite I would have expected. I will have to study this and experiment a little bit more.
To achieve a THD result of 0.002% @ 20kHz, I observed a BW of 160kHz and rise time of about 1us or less.
To address scottjoplin question, I would say this THD figure is a different one for each listener as expectation, demand and tolerance of each of us is different. Also this likely will also depend on the program material one is listening to as well as the speakers the amp connects to.
So for someone lets say THD 0.05% @ 20kHz is just fine while for someone else this is way past the tolerance level.
Thanks for taking the time and your explanation. The simulation result with limited rise time to 6µs is quite the opposite I would have expected. I will have to study this and experiment a little bit more.
To achieve a THD result of 0.002% @ 20kHz, I observed a BW of 160kHz and rise time of about 1us or less.
To address scottjoplin question, I would say this THD figure is a different one for each listener as expectation, demand and tolerance of each of us is different. Also this likely will also depend on the program material one is listening to as well as the speakers the amp connects to.
So for someone lets say THD 0.05% @ 20kHz is just fine while for someone else this is way past the tolerance level.
According to Wikipedia "distortion for a fundamental above 10 kHz is inaudible" Total harmonic distortion - Wikipedia
That would be correct concerning harmonic distortion alone, except that 10kHz + 11kHz into a "nonlinear mess" will result in a 1kHz IM product, which could be very audible. IM and HD are merely measurements, and the same circuit nonlinearities that generate HD will also generate IM. Given that most people listen to signals more complex than a pure sine wave, IM is an important consequence, and supersonic HF nonlinearities can have audible IM consequences at lower frequencies.
Just to beat a dead horse, this is also why it's helpful to filter away out of band inputs, since they can intermodulate back down to the audible band and have unfortunate consequences.
Generally, if the rolloff is inherent to the core, open loop structure of the amplifier, it will be detrimental.
If it is deliberately and stragetically added as I did, it will be beneficial (for the THD at least, but the BW will be limited).
When the loop gain is shaped and manipulated, it is somewhere in-between, and you can do wonders by packing a lot of gain where it matters, ie. in the audio range, to the detriment of higher frequencies, where (in principle) it does not.
It is a risky business though, because there can be numerous consequences on clipping behavior, etc., but designers of these older amplifiers were very smart, and managed to extract excellent performances from relatively limited hardware, as Discopete noticed.
For more modern alternatives, there is no need for hairy, difficult manipulations and faster (and linear) amplifiers generally do better regarding 20K distortion.
Is a good 20K performance actually necessary? That is mainly a matter of opinions, and tube lovers or Scott Joplin will probably say no, but that is a completely different debate....
Well, take this Wiki statement with a huge grain of salt. It's very easy switching a 10kHz signal on a function generator between sine and square wave and see if there is an audible difference. I guess this easy test would put this Wiki statement to rest.
Elvee
Well, I guess I am in the camp for whom a good 20KHz THD performance matters. As Monte McGuire suggests, we do listen generally to more complex signals than pure single frequency sine waves. If we assume that a complex 4kHz signal needs at least 5 harmonics to be reasonably well reproduced we are at 20kHz, yet the fundamental is right in the range where human hearing is sensitive. Therefore I believe THD at higher frequencies e.g. above 10kHz matters. However, this could be likely also be quite dependent on the program material that is listened to for example Jazz or Classic music vs. Electronic music.
And sure IMD matters a big deal too, but this is a different can of worms.😉
for the same peak voltage, it has to sound louder: the fundamental is Pi/2 times larger than for a sinewave, resulting in more than twice the power
The harmonics beyond 10k are irrelevant to what is audible, but the performance at these frequencies is not because of intermodulation distortion. If the THD at 20k is measurable, then so is the intermodulation between HF tones down to LF.
Any non linearity must generate both harmonic and intermodulation distortion.
It used to be quite common to quote THD at 1kHz and IMD at 17kHz+18kHz or similar pair of high frequencies - those two measurements together tell a lot and each measures at least some spurs that are in the audible range (whereas a 10+kHz THD doesn't).
But a plot of THD against frequency tells you even more (usually enough to indicate what the most prominent distortion mechanism of the amp is).
The actual effect of IMD is probably not what people generally think it is: using the 17+18kHz example, one could think that if the amp intermodulates badly, the result is going to be a prominent 1kHz product (difference).
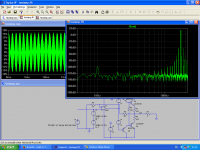
We can put this to test in the (deliberately) lousy test amp based on the LF opamp.
The amplitude of the two combined tones is close to clipping, and the 17~18kHz is sufficient to generate significant pre-slew distortion:
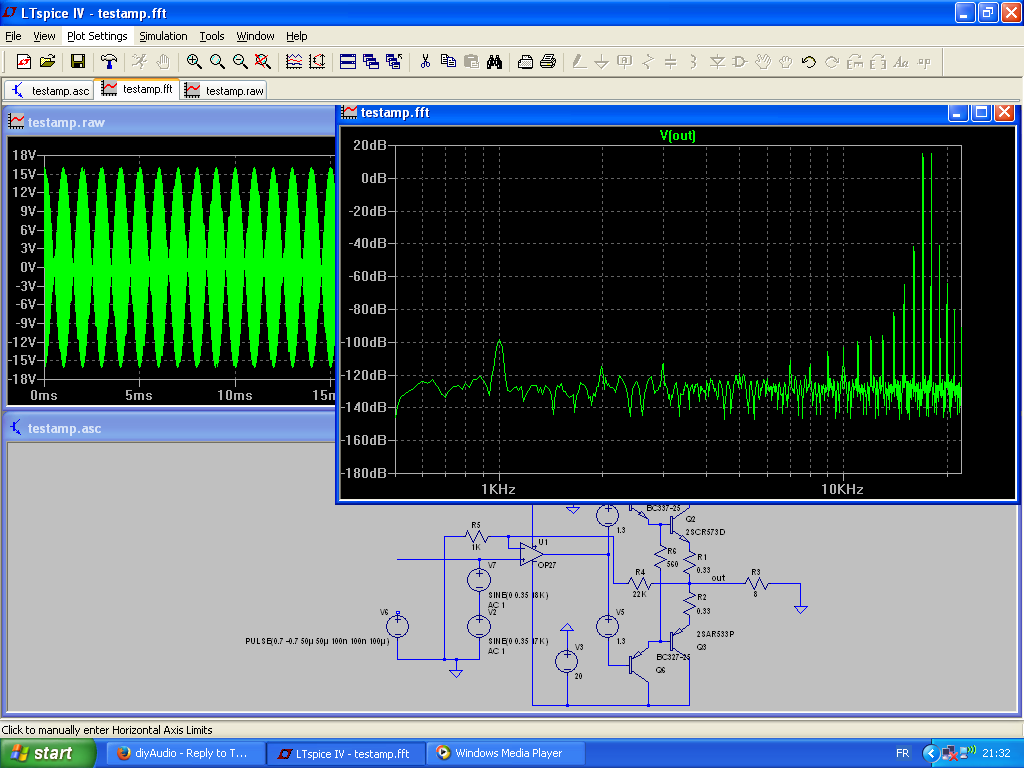
The 1kHz is indeed present, but its ampitude is >115dB down compared to the generating frequencies.
The largest IM products are much higher order ones, 16 and 19kHz about 60dB lower than the master tones.
Counterintuitive?
Yes, but we need to remember that at 1kHz, the lousy amp has plenty of loop gain, and is perfectly capable of burying that particular product in the noise.
Here is a sim showing the effect of a 1V/1kHz perturbation source:
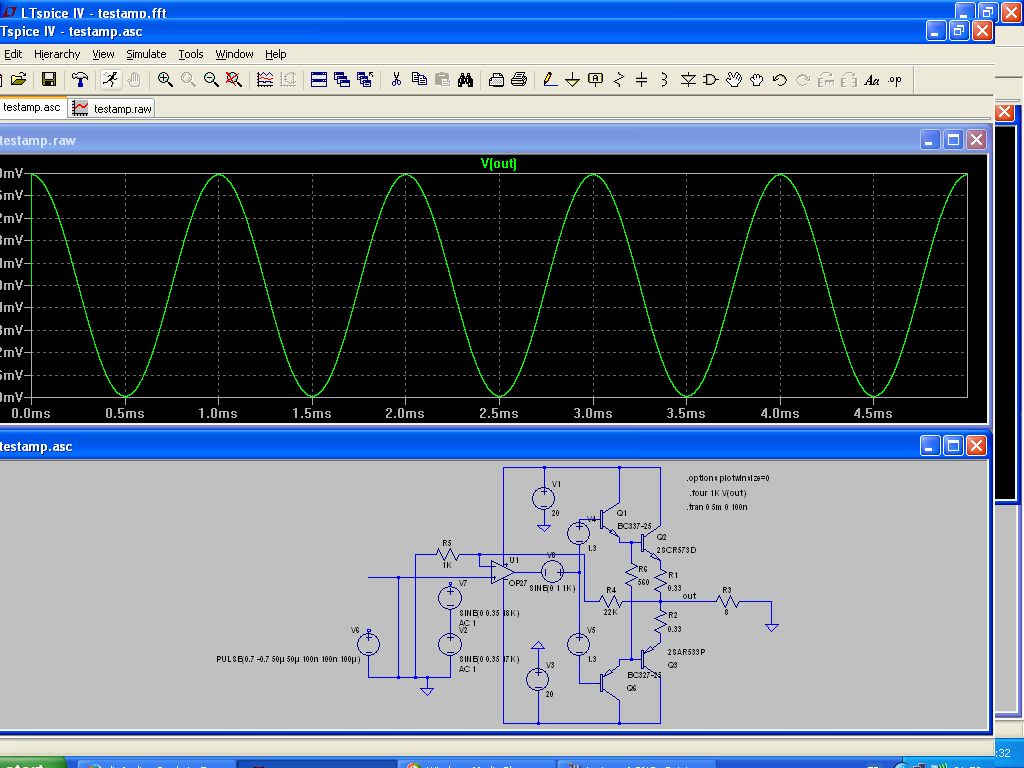
The resulting ouput amplitude is only 2mV, which means the rejection is 500x.
Higher order products have a much smaller initial amplitude, but they do not benefit from a similar loop gain, hence their prominence.
The conclusion that Scott would draw is that these products have no practical impact because they will be masked by the main tones, due to their proximity and lower amplitude.
We can put this to test in the (deliberately) lousy test amp based on the LF opamp.
The amplitude of the two combined tones is close to clipping, and the 17~18kHz is sufficient to generate significant pre-slew distortion:
The 1kHz is indeed present, but its ampitude is >115dB down compared to the generating frequencies.
The largest IM products are much higher order ones, 16 and 19kHz about 60dB lower than the master tones.
Counterintuitive?
Yes, but we need to remember that at 1kHz, the lousy amp has plenty of loop gain, and is perfectly capable of burying that particular product in the noise.
Here is a sim showing the effect of a 1V/1kHz perturbation source:
The resulting ouput amplitude is only 2mV, which means the rejection is 500x.
Higher order products have a much smaller initial amplitude, but they do not benefit from a similar loop gain, hence their prominence.
The conclusion that Scott would draw is that these products have no practical impact because they will be masked by the main tones, due to their proximity and lower amplitude.
