When considering the technical term of "directivity factor", I believe that it basically refers to the acoustic medium's rigid boundaries. As you know, us engineering types are always looking for situations where we can say, "although conditions do not match the ideal ones in the physical proof, such & such is close enough relative to some other stuff that we can just assume things are ideal and have an acceptable amount of error." So, at sufficiently low frequencies, things are "close enough" to free space to be treated as such, despite the presence of the enclosure. Similarly, at sufficiently high frequencies things get "close enough" to make assumptions about radiation into half-space given the enclosure's presence.
NOW, the effect of "beaming" seems like the next logical turn for this thread. Beaming (correct me since I am probably wrong here) seems to be a function of piston radius and frequency. As far as I can tell, it doesn't matter if the driver is in free space or half space. Maybe Beranek covers this...I haven't gotten that far yet though.
Originally Posted by weltersys:
There are no transducers in enclosures that are truly omni except at VLF, rendering an exact figure for baffle step compensation an academic exercise.
Art Welter
Let me add to my statement above:
Rendering an exact figure for baffle step compensation an academic exercise unless all of the enclosure and driver dimensions are taken in to account, as well as the distance said cabinet is from any boundaries, and the inherent directivity of the driver at frequencies around the point where the baffle step occurs.
In other words, measurement of the loaded cabinet is crucial in the design of any proper baffle step compensation.
Art Welter
There are no transducers in enclosures that are truly omni except at VLF, rendering an exact figure for baffle step compensation an academic exercise.
Art Welter
Your graph nicely shows what has happened with a specific 5" unit on a 8" x 14" baffle of unknown (to us) cabinet depth and distance to boundaries.Hi,
Yes there are in the case of small speakers away from walls (for imaging)
where you do see the full baffle step occurring, typically takes from the
low one hundreds up to around 1K, you get a full 6dB baffle step, and
typically a further baffle peak of around 2dB at the top end to boot.
(only a sphere with a tiny driver gives a the classic 6dB transition)
5" unit on a 8" x 14" baffle (ZaphAudio ZMV5)
Its not academic and the speakers are omnidirectical below ~ 100Hz.
Room gain arrives too low to help, but can bolster the bass roll if the
speaker is designed with a slow bass roll-off to properly utilise it.
rgds, sreten.
Let me add to my statement above:
Rendering an exact figure for baffle step compensation an academic exercise unless all of the enclosure and driver dimensions are taken in to account, as well as the distance said cabinet is from any boundaries, and the inherent directivity of the driver at frequencies around the point where the baffle step occurs.
In other words, measurement of the loaded cabinet is crucial in the design of any proper baffle step compensation.
Art Welter
Yes, “a few dB of drop at 90 degrees” does indicate some directivity from the box.
Tom Danley’s Bdeap 4 box array with an on axis sensitivity of 117.5 dB SPL with 1 electrical watt at 1 meter, measured in half space has what I would call significant LF directivity, 5.5 dB over 1 acoustic watt, which you wrote is 112dB for a half space hemispheric source.
Art
Many of the simpler baffle diffraction simulators don't fully simulate the 3 dimensional aspects of diffraction - they don't account for diffraction off adjacent drivers, typically don't use a 3D model for the driver at all, (just a flat piston in a baffle rather than a cone shape, which is wrong for estimating driver directivity as well) and also don't allow you to specify the depth of the cabinet, nor its shape beyond the shape of the front baffle.
When I've pointed out these deficiencies to people taking the simulated results as gospel I just get shrugged shoulders and insistence that the simulators are more than accurate enough. Well, fine...I think I'll follow up any simulations with measurements all the same. To be fair, some simulators are better than others, but I'm doubtful that any of the readily available (eg free/inexpensive) ones do a truly accurate full 3D model of the problem, and even if they model the geometry of the driver they can't model the directivity of the driver without extensive driver measurement data. By the time you have that measurement data you might as well have just measured the baffle step response directly.
It's surprising how many people think that baffle step means an exact 6dB increase at all frequencies above the baffle step frequency, like a shelf response. (Ignoring ripple for the moment) In fact you'll only get 6dB if the directivity of the driver is maintained to greater than 180 degrees well above the baffle step frequency, as the gain comes from constraining the radiation angle - if the driver is already narrower than 180 degrees the gain will be less. If its a lot narrower than 180 degrees there will be no gain at all.
This is particularly evident with large full range drivers. Put an 8" full range driver on a half metre wide baffle (vs the end of a cylinder) and you'll see baffle step starting to take effect around 240Hz, a maximum amount around 500-1000Hz, then by the time you get to 2Khz and above the baffle has almost no effect, because the radiation angle of the driver is so much less than 180 degrees. The wide baffle ends up putting a big "hump" in the midrange rather than shelving up the entire high frequency response.
The way I like to look at it is a baffle is basically a 180 degree wave-guide.
Just like the mouth size of a wave-guide dictates it's lower cut-off frequency, the baffle size also dictates the lower cut-off frequency where "pattern control" is maintained to, the same types of ripples in response near the cut-off frequency of a sharp edged baffle occur as occur in a waveguide with a sharp improperly terminated mouth, and just as a wave-guide only provides "gain" at the low frequency end above its cut-off, gradually falling to no gain at frequencies where the driver itself is starting to beam, so does a baffle, with a potential maximum 6dB gain just above its cut-off (ignoring ripple) eventually falling to nothing by the time the frequency is high enough for the driver to be beaming on its own accord.
None of the free baffle diffraction simulators I've tried show the real-life fall in baffle gain at high frequencies due to the directivity increase of the driver, even though they all ask for the diameter of the driver, and should at least be able to approximate it. I can only assume from this that the models are far too simplistic.
Hi,
Completely wrong pragmatically. The directivity of larger drivers working well
into there break up regions implies even more axial gain that is reflected in
the typical 2pi "infinite baffle response" of the driver as an axial response rise.
As the speed of sound in cones typically far exceeds that of air, BSC is all
too real for most drivers as they will be effectively pistonic related to the
baffle size, what is the problem in simply accepting this ? its true .....
rgds, sreten.
Just to be clear, my original post was intended to be an academic exercise. I was bothered because my understanding of the physics was unclear, and I wanted to run a proof on the "ideal" physical phenomena. Real-world drivers and environments are a fair bit more complicated, of course.
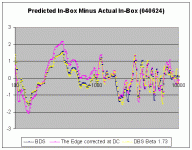
Not so fast! I have. 🙂
Using Seas measurements taken from their anechoic chamber, please see attached. I think the high frequency error is due to diffraction of the adjacent driver in cabinet, not due to the models.
Dave
Simulator settings:
Bjorn Input, all measures:
Mic location: Center of the tweeter (all 60x80 measures, including 041202 and 040624 and tweeter in-box).
Note: both BDS and Jeff’s simulator place the mic in x/y space directly opposite the driver.
Simulator Settings For 60x80 Baffle (only 1m shown)
Simulator Settings
BDS:
Frequency Support
Real Piston Drive Simulation: Dome Tweeter
centimeters
quadruple sample
sharp edge
combined source
quadrangle shape
separate type
edge size 0
axis distance 100
axis angle 0
baffle tilt 0
baffle co-ords: (-40, 70), (-40, 10), (40, 70), (40, 10)
driver co-ords: height 47.5, displace 10
The Edge 1.8:
Baffle size 800(x) x 600👍 mm
#corners = 4
#speakers =1
edge sources = 80
speaker source density = 10
mic distance 1m
speaker circular shape, 30.9mm size
mic directly over speaker at x= .5003 and y = 0.3736
The Diffraction and Boundary Simulator (Beta 1.73):
Baffle size 31.496” (width) x 23.622”(height)
Speaker location x= 19.665” and y = 14.709”
Baffle edge radius = sharp edge source
Speaker Piston Diameter = 1.217”
Baffle tilt angle = 0.0 degrees
Listening Axis = 3.281 feet
Axis Angle 0.0 degrees (sets the mic in (x,y) directly opposite the driver)
SPL View:
100 points per decade, 100 to 10 kHz, Log Distribution
Simulator Settings For In-Box
BDS:
Frequency Support
Real Piston Drive Simulation: Dome Tweeter
centimeters
quadruple sample
complex edge
combined source
quadrangle shape
separate type
edge size 1.2
axis distance 100
axis angle 0
baffle tilt 0
baffle co-ords: (-10, 59.6), (-10, 10), (10, 59.6), (10, 10)
driver co-ords: height 53.1, displace 0
The Edge 1.8:
Baffle size 200(x) x 496👍 mm
#corners = 4
#speakers =1
edge sources = 80
speaker source density = 10
mic distance 1m
speaker circular shape, 30.9mm size (30.9mm dia = 7.5 sq cm)
mic directly over speaker at x= .0984 and y = 0.4296
The Diffraction and Boundary Simulator (Beta 1.73):
Baffle size 7.874” (width) x 19.528”(height)
Speaker location x=3.937” and y =16.970”
Baffle edge radius = 0.47”
Speaker Piston Diameter = 1.217”
Baffle tilt angle = 0.0 degrees
Listening Axis = 3.281 feet
Axis Angle 0.0 degrees (sets the mic in (x,y) directly opposite the driver)
SPL View:
100 points per decade, 100 to 10 kHz, Log Distribution
From Seas, the test cabinet:
The box outside dimensions:
Front baffle: 20cm wide and 49.6cm high
Box depth: 29.6cm
Edges are trimmed with a roundover-bit r=12mm.
Driver placement:
Both drivers are centered on the vertical axis.
The distance between the drivers centers are 158.5mm
The distance from the top of the baffle to the tweeter centre: 65mm (ie y =431 from bottom)
The distance from the top of the baffle to the woofer centre: 223.5mm
The microphone (B&K 4133) was placed 1 meter from the front of the speaker, on the tweeter axis. The microphone was not moved during the whole measurement session. The woofer measurements are also done with the microphone centered on the tweeter axis. The reason for doing this is that the relative phase difference between woofer and tweeter will be accurately stored in the measurements.
Last edited:
Wow, cool! Thanks. It looks like the BDS sheet does in fact give pretty good estimates. What sort of room was this done in? What sort of windowing was applied to the measurement (if any) to deal with room reflections?
Fine by me.
Take a look at the constant directivity horn papers of Keele or Henricksen. They found that the typical CD shape was a straight sided waveguide (hopefully with end flaring) with two dimensions that mattered: the diffraction gap or driver diameter feeding it, and the overall width. Between those two dimensions (or related wavelengths) you had constant directivity. The feeding diameter, necessarily smaller, determined the max frequency of beamwidth control and the unit beamed above that frequency. The horn diameter created the low frequency limit. Below that dimension beamwidth expanded again. The bandwidth of opertion was related to the ratio of outer to inner dimensions.
http://www.xlrtechs.com/dbkeele.com/PDF/Keele (1975-05 AES Preprint) - Whats So Sacred Exp Horns.pdf
Obviously a cabinet is a more-or-less constant directivity waveguide set for 180 degree radiation. The outer to inner dimension ratio is seen as the baffle size to driver diameter. High frequency beaming may be a function of the driver, but low frequency directivity is all down to cabinet dimensions.
David S.
I know we've moved on, but ran across this paper on Don Keele's site.
http://www.xlrtechs.com/dbkeele.com...S Preprint) - Max Efficiency of Speakers.pdf
He finds that drivers of a given size have a maximum possible efficiency (2.5% for a 12" unit) and that it is related to to the ratio of moving mass to air load mass. This explains what was seen in the Gander and Keele measurements with 4 or 9 woofers. True efficiency goes up as driver area increases or number of drivers increases, but there is an upper limit.
Don shows that Thiele/Small calculations overestimate efficiency because airload is significant (above 0.6% efficiency) and should be added to observed moving mass.
Warning: contains Acoustic Impedance curves.😉
David
http://www.xlrtechs.com/dbkeele.com...S Preprint) - Max Efficiency of Speakers.pdf
He finds that drivers of a given size have a maximum possible efficiency (2.5% for a 12" unit) and that it is related to to the ratio of moving mass to air load mass. This explains what was seen in the Gander and Keele measurements with 4 or 9 woofers. True efficiency goes up as driver area increases or number of drivers increases, but there is an upper limit.
Don shows that Thiele/Small calculations overestimate efficiency because airload is significant (above 0.6% efficiency) and should be added to observed moving mass.
Warning: contains Acoustic Impedance curves.😉
David
Last edited:
Even a rigid cone has increasing directivity at high frequencies, cone breakup is not required. In fact cone breakup done properly tends to reduce directivity increase at high frequencies vs an equal diameter rigid cone. (Effective in-phase radiating area shrinks at higher frequencies, increasing dispersion...)
In any case, what you say is wrong - it doesn't imply anything of the sort. The "gain" of the baffle comes from constraining the radiation angle of the driver. If the drivers radiating angle is already narrow there is nothing to constrain.
It's wrong to assume that beaming of a driver at high frequencies will result in an axial increase in response, because that assumes that the power response doesn't fall off significantly. In many extended range drivers the power response is designed (through both cone losses, and voice coil inductance) to fall off at a complimentary rate to the increase in directivity to maintain a flat axial response on a baffle. If the two don't match you will get either a rising or falling axial response at high frequencies.
A better way to look at the problem of baffle step is to treat it as a loss below a certain frequency, not a gain above a certain frequency, and realise that any finite sized driver cannot radiate into 4pi space at high frequencies, because the cone itself becomes a "minimum size" baffle.
If you have a 12" woofer the cone itself (plus frame) forms a 12" circular baffle which sets a finite minimum possible baffle size, therefore a finite maximum baffle step frequency, above which the radiation angle is constrained.
Thus varying the width of an actual baffle from the narrowest possible (the driver width) such as a small cylinder, to a much wider one will only boost middle frequencies. Very high frequencies will not be affected nor will very low. That was my point.
Many drivers are designed with the assumption of an infinite baffle which means their top end power response is usually set to roll off in a complementary fashion to their overall directivity on an infinite baffle (baffle + inherent driver directivity) to maintain a flat axial response as closely as possible, but it isn't necessarily the case.
I don't understand what you're trying to say here ? What relevance is the speed of sound in the cone to this problem ? Yes BSC is very real, however its not a nice neat 6dB shelf based only on the size of the baffle, the directivity of the driver is a controlling factor at the high end well past the baffle's cut-off frequency.
Last edited:
There is one practical difference between the wave-guide and the baffle though - the driver in a waveguide is usually (always ?) symmetrically located in the middle, whilst a driver on a baffle is typically not right in the middle, usually on purpose.
What is the effect of this on the pattern control of the baffle near the cut-off frequency ? Obviously it affects the shape of the diffraction ripples, but does moving a driver closer to the edge of a baffle increase the effective baffle step frequency somewhat as well ?
Last edited:
Uh, failing to account for diffraction of adjacent drivers is a problem with the modelling, surely ?
Thanks for helping to prove my point for me anyway, as apparently even the best simulator of the 3 tested has an error magnitude of +/- 1.5 dB through the transition region, (+/- 2dB for the worst one) which is pretty high when you consider the overall transition is only 6dB, that error magnitude is far too high to design a crossover against without measurement.
It would have been helpful if we could have seen the actual measured response and simulated response overlaid rather than just a differential error so that we could see the true nature of the errors.
For example the fact that the error deviation went negative then positive by a similar amount through the transition region suggests that the slope and/or the corner point for the transition was incorrectly calculated.
Likewise in the region above 2Khz we don't know what the source of the error is from only an error difference graph. My guess is that the simulation predicted narrow band ripples that simply failed to materialize in the measurement due to a simplified (or non existant) geometrical driver model that failed to predict the correct driver directivity.
As I've said on other threads discussing similar points, its a useful "first pass" to simulate possible "what if" cabinet scenarios but its not accurate enough to design a crossover against without measuring the driver on the actual baffle.
I find this comment interesting in the ARTA application note where it discusses how to merge a near-field response with a far-field response, and the "simplistic" (non-geometrical) baffle step estimation used in ARTA:
"Note: ARTA and STEPS uses the previous expression for the estimation of the diffraction for spherical
or rectangular baffled boxes. Some CAD and simulation programs are using a high-frequency
geometrical model for the estimation of box diffraction at low frequencies. Such models can give
larger errors on low frequencies than the simple model that is presented here. "
http://www.fesb.hr/~mateljan/arta/AppNotes/AP4_FreeField-Rev03eng.pdf
Ivo is a pretty smart guy, and yet seems skeptical of the accuracy of current geometric baffle step models...
Last edited:
Stick a sensitive microphone in front of it and feed it back to the driver's input: Voila! Perpetual motion!😉
David
I'm okay with that. If the simulaters are accurate enough to guide you to a box shape and driver placement that result in the smoothest response, then that is a good result.
I would expect to measure the drivers on the cabinet anyhow, but now there is only one cabinet to build.
David S.
Don't forget that the air load also flattens out at ka greater than 1. That puts an automatic 12 dB/Octave rolloff in power response, that may or may not be counteracted by directivity.
(I'm really into this acoustic impedance thing now.)😀
David
Hmm, it can't be fully compensating for increases in directivity, otherwise it wouldn't be possible to make a full range driver that has an axial response that steadily climbs from midrange to treble by 10dB or more - something that some of the FR units with copper shorting rings and low VC inductance do.
Interestingly, non-copper ring variants of the same driver (with identical cones) typically have a treble response that's relatively level, perhaps even falling slightly suggesting that voice coil inductance is a major factor in counteracting axial response rise when the driver starts beaming, by rolling off the power response...
If you're enjoying yourself, have a look at the ARTA application note I just linked to - it has a whole bunch of mathematical derivations of near-field to far field and half space to full space transitions that are way over my head 😀
If axial response climbs directivity is not only compensating, it is overcompensating for power response drop.
But don't be fooled, every full range driver, no matter how extended its on-axis response, falls like a stone off axis.
David
Umm, that's what I was trying to say, maybe I didn't say it too well.
In response to your comment that power response would fall at high frequencies due to air load, I was saying that it can't be falling enough from that alone to compensate for directivity increase, otherwise a steadily upwards axial response slope wouldn't be possible.
To get a flat axial response in this region of directivity increase there needs to be further power response roll off from other factors such as VC inductance.
Last edited:
- Status
- Not open for further replies.