I've seen people recommend the use of this calculation/formula but I don't get why?
What is the following calculation supposed to tell us;
1) take the turns ratio of the output transformer and square it
2) then take the above result and multiply it by the ohms of the speaker that the output transformer will be connected to.
Example, the output transformer has a turn ratio of 5.1 so the first step above is to square that which gives you 26.01. So next you multiply that number (26.01) times the impedance of the speaker, in this example a 23 ohms speaker...and that gives you 598.23.
So what is the purpose of calculating that 598.23 number? I know they somehow use that number (598.23 in this example) to determine the electrical parameters (i.e. primary ohms, secondary ohms) of the output transformer that they should put in their tube amp design. But how does one use that number (598.23 in this example) to determine what the electrical specs of the output transformer should be? How is that calculated number useful?
What is the following calculation supposed to tell us;
1) take the turns ratio of the output transformer and square it
2) then take the above result and multiply it by the ohms of the speaker that the output transformer will be connected to.
Example, the output transformer has a turn ratio of 5.1 so the first step above is to square that which gives you 26.01. So next you multiply that number (26.01) times the impedance of the speaker, in this example a 23 ohms speaker...and that gives you 598.23.
So what is the purpose of calculating that 598.23 number? I know they somehow use that number (598.23 in this example) to determine the electrical parameters (i.e. primary ohms, secondary ohms) of the output transformer that they should put in their tube amp design. But how does one use that number (598.23 in this example) to determine what the electrical specs of the output transformer should be? How is that calculated number useful?
That is the load that the output tube sees. Transformers are designed for a specific input and output impedance,
as well as a particular turns ratio, to optimize distortion, power, and bandwidth.
http://knob.planet.ee/kirjandus/books/Wolpert_Audio_Xfmr_Design_Manual.pdf
https://www.jensen-transformers.com/wp-content/uploads/2014/08/Audio-Transformers-Chapter.pdf
as well as a particular turns ratio, to optimize distortion, power, and bandwidth.
http://knob.planet.ee/kirjandus/books/Wolpert_Audio_Xfmr_Design_Manual.pdf
https://www.jensen-transformers.com/wp-content/uploads/2014/08/Audio-Transformers-Chapter.pdf
Last edited:
so does that mean that the ohms of the secondary can be 4 ohms or 2,000 ohms and it makes no difference because the tube will only see 598.23 regardless of which tap the speaker is hooked up to on the secondary. Some secondary taps have a center tap at 75 ohms and the other tap is 150 ohms. Sounds like it doesn't matter what the ohms are of the secondary tap because no matter what, the tube will see it as 598.23?
Think of the transformer as a black box that converts the load (speaker) into a much higher impedance to which the tube can deliver useful power. No output tube can power a speaker directly because the impedance of the tube is much higher than the impedance of the speaker (as they are currently designed). The tube signal voltage is stepped down to the load (by the turns ratio), and the tube signal current is stepped up to the load (by the turns ratio.) Check out links in post #2.
Last edited:
You should've attached this to your other post, as it's a continuation of that conversation.
When a transformer is designed/made, the turns ratio in combination with the winding geometry are carefully balanced to obtain good performance at the impedances specified for the primary and secondary windings. As you stray from those impedances, the leakage inductance and interwinding capacitance will start to do funny things to the frequency response. A general lack of primary inductance may also screw up low frequency response.
If we consider your 23 ohm load:
On a 10K:16 ohm transformer (which is what I recommended you purchase in your other thread), that's a 25:1 step-down ratio (voltage) and 625:1 step-down ratio (impedance). With your 23 ohm headphones on the 16 ohm tap, the reflected impedance pops up to 14K for the whole winding. This is reasonably close to the design center of 10K:16 and you could even put an extra resistor across the secondary to bring down that reflected load to 10K if you wanted to.
On a 10K:150CT transformer running your 23 ohm headphones off the center tap, your impedance ratio is 10K:75 or 133:1, resulting in a 3K load reflected back to the tubes for the whole winding.
What I would suggest is reading up on drawing load lines, then look at a 1.5K load line for a 6DJ8 vs. a 7K load line for a 6DJ8 (just draw them as resistive loads that go to twice B+).
When a transformer is designed/made, the turns ratio in combination with the winding geometry are carefully balanced to obtain good performance at the impedances specified for the primary and secondary windings. As you stray from those impedances, the leakage inductance and interwinding capacitance will start to do funny things to the frequency response. A general lack of primary inductance may also screw up low frequency response.
If we consider your 23 ohm load:
On a 10K:16 ohm transformer (which is what I recommended you purchase in your other thread), that's a 25:1 step-down ratio (voltage) and 625:1 step-down ratio (impedance). With your 23 ohm headphones on the 16 ohm tap, the reflected impedance pops up to 14K for the whole winding. This is reasonably close to the design center of 10K:16 and you could even put an extra resistor across the secondary to bring down that reflected load to 10K if you wanted to.
On a 10K:150CT transformer running your 23 ohm headphones off the center tap, your impedance ratio is 10K:75 or 133:1, resulting in a 3K load reflected back to the tubes for the whole winding.
What I would suggest is reading up on drawing load lines, then look at a 1.5K load line for a 6DJ8 vs. a 7K load line for a 6DJ8 (just draw them as resistive loads that go to twice B+).
If you start with a specific transformer (in your case 5:1 turns) *and* a specific load (23 ohms) then the primary impedance of your transformer *is* fixed and given as 600 ohms.
Now you can use that number to find an amplifier design (architecture/e.g.circuit *and* components/e.g.tubes) which can drive these 600 ohms with the required power to make it loud enough *and* with acceptably low distortion.
A SRPP style amp with small power tubes may be able to drive 600 ohms, a single ended small signal tube will not.
So the number tells you how to design your amp or what amp to choose.
More often people start with the design of the amp and choose the tubes they want to use, calculate or ask the designer what impdance it is able to drive to get the desired power and distortion level and *then* they look for a transformer whose properties suit these requirements.
In this case, if the amp designer or your calculations tells you that this particular amp works best with a primary impedance of e.g. between 10...15 kohms then you can use your formula *backwards* to determine the turns ratio. So 10k:23R=435 the square root of which is 20 gives a 20:1 turns ratio as the low end and 15k:23R=652 the square root of which is 25 gives a 25:1 turns ratio as the upper end of the range.
By the way, no need to calculate to 0.1 precision ...
Now you can use that number to find an amplifier design (architecture/e.g.circuit *and* components/e.g.tubes) which can drive these 600 ohms with the required power to make it loud enough *and* with acceptably low distortion.
A SRPP style amp with small power tubes may be able to drive 600 ohms, a single ended small signal tube will not.
So the number tells you how to design your amp or what amp to choose.
More often people start with the design of the amp and choose the tubes they want to use, calculate or ask the designer what impdance it is able to drive to get the desired power and distortion level and *then* they look for a transformer whose properties suit these requirements.
In this case, if the amp designer or your calculations tells you that this particular amp works best with a primary impedance of e.g. between 10...15 kohms then you can use your formula *backwards* to determine the turns ratio. So 10k:23R=435 the square root of which is 20 gives a 20:1 turns ratio as the low end and 15k:23R=652 the square root of which is 25 gives a 25:1 turns ratio as the upper end of the range.
By the way, no need to calculate to 0.1 precision ...
So, since all the commentary above is factually correct, here's the redux: Transformers transform the primary to the secondary, and the secondary to the primary. Got that? Transformers are necessarily bidirectional.
To understand why a 5.1 to 1 ratio of primary-to-secondary has a 5.1² or 26× transformation of impedance, consider the lowly resistor as a power eating device.
If we have a 100 Ω resistor, and put 10 volts across it, due to Ohm's Law (E = IR), we see that
But what about the Z² (impedance squared) idea? That turns up in this way. Lets use our resistor again, the 100 Ω job. Setting the power at 1 W (the first example), we had:
EOUT = 1/k EIN … and
IOUT = k IIN … so
ROUT = 1/k EIN / k IIN
ROUT = 1/k² EIN / IIN, and substituting Z for the EI business:
ROUT = 1/k² ZIN ... And vice-versa!There's your k² or ratio² relationship. Mathematically shown.
Hope that helps, and if not, I apologize for taking all y'all's time.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
To understand why a 5.1 to 1 ratio of primary-to-secondary has a 5.1² or 26× transformation of impedance, consider the lowly resistor as a power eating device.
If we have a 100 Ω resistor, and put 10 volts across it, due to Ohm's Law (E = IR), we see that
E = IR … rearranged to
I = E/R … and with E = 10 V, R = 100 Ω
I = 10 ÷ 100 amps
I = 0.10 A
Now, using the resistive power formulaI = E/R … and with E = 10 V, R = 100 Ω
I = 10 ÷ 100 amps
I = 0.10 A
P = IE
P = 0.10 A × 10 V
P = 1 W
Our lil' power eater will be heating up with 1 watt of power dissipated thru it. To carry this further, with 20 volts:P = 0.10 A × 10 V
P = 1 W
I = E/R
I = 20 V ÷ 100 Ω
I = 0.20 A
And thru the power formulaI = 20 V ÷ 100 Ω
I = 0.20 A
P = IE
P = 0.20 A × 20 V
P = 4 W
You can see that as far as power goes, doubling the voltage quadruples the power generated thru the resistor, all other things being equal. Perhaps this will make it more clear then, how a transformer might have a 5.1 : 1 ratio between windings (note that I'm specifically not saying 'primary' and 'secondary'), given that a transformer's unique ability is to transform powerP = 0.20 A × 20 V
P = 4 W
VIN • AIN = kVOUT • AOUT/k … where
k = turns ratio of (IN over OUT) windings
shows that the voltage change and the current change are inversely in proportion to each other, yet the net is still 'VA' because the 'k' cancels. Transformers transform power. k = turns ratio of (IN over OUT) windings
But what about the Z² (impedance squared) idea? That turns up in this way. Lets use our resistor again, the 100 Ω job. Setting the power at 1 W (the first example), we had:
P = IE … and
E = IR … so substitute in
P = E²/R or
P = I²R
They're both equivalent. So, using the idea that a transformer's transformation of power is nearly ideal to pass-thru, we getE = IR … so substitute in
P = E²/R or
P = I²R
P = E²/R … is
PR = E²
R = E²/P
Right? Working just with the transformer's EIN IIN = kEOUT • IOUT/k identity above, we getPR = E²
R = E²/P
RIN = EIN / IIN
on one side, andROUT = EOUT / IOUT
which now substitutesEOUT = 1/k EIN … and
IOUT = k IIN … so
ROUT = 1/k EIN / k IIN
ROUT = 1/k² EIN / IIN, and substituting Z for the EI business:
ROUT = 1/k² ZIN ... And vice-versa!
Hope that helps, and if not, I apologize for taking all y'all's time.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
Last edited:
A transformer has a turns ratio that determines how the impedances on the primary and secondary side are related. I have published a few simplified articles about this subject, see:
Impedance matching of loudspeakers to output valves. – tubes and
Output transformers and push-pull stages. – tubes
Impedance matching of loudspeakers to output valves. – tubes and
Output transformers and push-pull stages. – tubes
Last edited:
so does that mean that the ohms of the secondary can be 4 ohms or 2,000 ohms and it makes no difference because the tube will only see 598.23 regardless of which tap the speaker is hooked up to on the secondary. Some secondary taps have a center tap at 75 ohms and the other tap is 150 ohms. Sounds like it doesn't matter what the ohms are of the secondary tap because no matter what, the tube will see it as 598.23?
The output transformer primary always sees output speaker impedance times turns ratio squared.
So the output load always reflects back to the primary proportional to turns ratio squared.
How is that calculated number useful?
that is the load that the primary of the traffo presented to the output amplifier when 23 ohm secondary is connected...
Thank you Nigel Wright. So then is the objective of the tube amp designer to select parts that will cause the primary of the OT to see the speaker as having an impedance that matches the ohms of the secondary? In other words, if the secondary tap is 600 ohms, then the speaker can be 23 ohms as long as the turn ratio is such that it causes the primary to see the speaker as a 600 ohm.
Example; OT IS 15K ohms at primary with 600 ohm at secondary with a 5.1 turns ratio...if I understand you nigelwright, the ideal speaker is 23 ohms because 5.1 squared is 26.01...and 26.01 x 23 = 598.23...so 598.23 is very close to a perfect match. A 600 ohm speaker is a poor match because 26.01 X 600 is 15,606...WHAT?? So do you want to match the speaker to the 15K or the 600 ohm.?
Example; OT IS 15K ohms at primary with 600 ohm at secondary with a 5.1 turns ratio...if I understand you nigelwright, the ideal speaker is 23 ohms because 5.1 squared is 26.01...and 26.01 x 23 = 598.23...so 598.23 is very close to a perfect match. A 600 ohm speaker is a poor match because 26.01 X 600 is 15,606...WHAT?? So do you want to match the speaker to the 15K or the 600 ohm.?
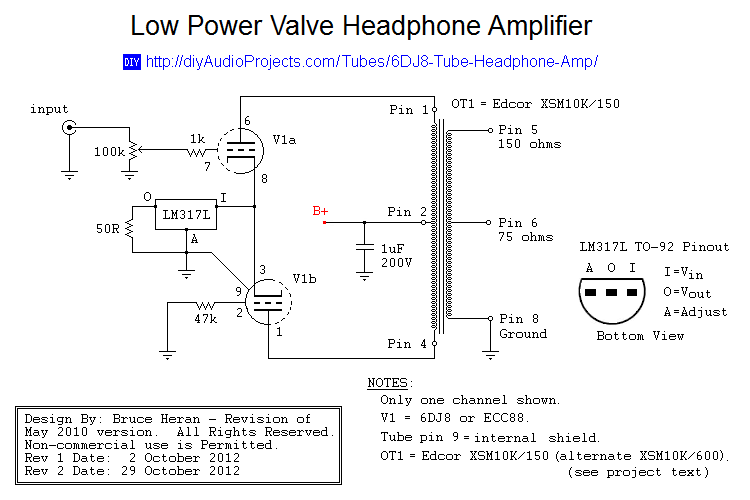
ah that is a tube amp?
so then the choice of the output transformer is based on the plate resistance of the output tube, the b+, and the output swing...
will 600 ohms be a right load for the tube? that is the question for you...
if you show as your scheme we will be able to advise you...
turns ratio is key....
5 to 1 turns ratio is fixed. the impedance ratio is 25 to 1..
15k to 600
600 ohm to 24 ohms..
5k to 200
2.5k to 100
the above have the same impedeance ratio of 25
so then the choice of the output transformer is based on the plate resistance of the output tube, the b+, and the output swing...
will 600 ohms be a right load for the tube? that is the question for you...
if you show as your scheme we will be able to advise you...
turns ratio is key....
5 to 1 turns ratio is fixed. the impedance ratio is 25 to 1..
15k to 600
600 ohm to 24 ohms..
5k to 200
2.5k to 100
the above have the same impedeance ratio of 25
Last edited:
Output transformers usually come with a primary impedance rating and a secondary impedance rating or even multiple secondary impedance ratings if there is more than one secondary tap.
i.e. a 3200ohm primary with 4, 8 and 16 ohm secondary taps.
Output transformers also have a power rating so the wire is made thick enough not to fuse on full power.
i.e. a 3200ohm primary with 4, 8 and 16 ohm secondary taps.
Output transformers also have a power rating so the wire is made thick enough not to fuse on full power.
No output tube can power a speaker.
Julius Futterman, were he around, might take issue with that.
Julius Futterman, were he around, might take issue with that.
There is a “technical limit” of what a valve may power, based on its allowable plate (anode) heating, the supply voltage, and its internal so-called “plate resistance”. In ideal terms, a valve “at saturation” can be viewed as a resistor in series with a load (speaker or output transformer), in series with the B+ supply.
So, for the sake of discussion, let's say a valve's at-saturation plate resistance is 5,000 Ω. B+ is 300 V. Our “speaker” is 8 Ω.
E = IR … rearranging
I = E/R … E = 300 VB+, R = (5,000 RA ⊕ 8 RSPKR)
I = 0.0599 A (≈ 60 mA)
VR = ⁸⁄₅₀₀₈ × 300
VR = 0.48 V
P = IE power formula
P = 0.0599 A × 0.48 V
P = 0.0288 W or 29 mW
This, while not “exciting” would be the limit of power delivered by the hypothetical 5000 Ω plate-resistance valve to an 8 Ω in-series load, whether presented at the cathode or anode!.I = E/R … E = 300 VB+, R = (5,000 RA ⊕ 8 RSPKR)
I = 0.0599 A (≈ 60 mA)
VR = ⁸⁄₅₀₀₈ × 300
VR = 0.48 V
P = IE power formula
P = 0.0599 A × 0.48 V
P = 0.0288 W or 29 mW
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
PS: “OTL” type amplifiers 'work' by using multiple low RA valves in parallel, at modest B+ voltages not to exceed valve-manufacturer max PA plate dissipation. With RA at only 750 Ω, 4 devices in parallel, PSPKR on a 300 V B+ supply is 4.9 W. However, the “stack” is dissipating 235 W nominal, or 59 W/valve. Rather more than even the most aggressive valves one normally finds on the dusty shelves of the used-tube aisle.
⋅-=≡ GoatGuy ✓ ≡=-⋅
PS № 2, just as a thought then, substituting a step-down transformer for the 8 Ω load, above, of say 5 to 1 winding (25 to 1 impedance), with the same 8 Ω speaker,
I = E/R … E = 300 VB+, R = ((750 Ω ÷ 4 ea RA) + (25 × 8 RSPKR))
I = 0.3159 A (≈ 316 mA)
VR = (25 Z multiplier × 8 ohm) / ( 750 ÷ 4 + 25 × 8 ) × 300
VR = 154 V
P = IE power formula
P = 0.316 A × 154 V
P = 49 W
I = 0.3159 A (≈ 316 mA)
VR = (25 Z multiplier × 8 ohm) / ( 750 ÷ 4 + 25 × 8 ) × 300
VR = 154 V
P = IE power formula
P = 0.316 A × 154 V
P = 49 W
See how much good a tranformer does at capturing the available power of a bunch of tubes? NOTE … do not use this calculation as if it were an oracle. Real world power is related to VRMS, which is closely related to the VB+ used above, but between 30% to 35% of what you might expect, in power. ⋅-=≡ GoatGuy ✓ ≡=-⋅
Last edited:
so does that mean that the ohms of the secondary can be 4 ohms or 2,000 ohms and it makes no difference because the tube will only see 598.23 regardless of which tap the speaker is hooked up to on the secondary. Some secondary taps have a center tap at 75 ohms and the other tap is 150 ohms. Sounds like it doesn't matter what the ohms are of the secondary tap because no matter what, the tube will see it as 598.23?
That 598.23 is not a quantity, it is a ratio. It is the factor you need to multiply the secondary load by to get what the tube sees at the primary. Hence the word 'transformer'.
So with 8 ohms, the tube sees 8 X 598.23; with 100 ohms load, the tube would see 100 X 598.23.
Jan
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
Don't be a clown with this red herring stuff, one might mistake you for an educated eejit. You pick the valve for the job and if need be put them in parallel as you subsequently added.
Julius Futterman, were he around, might take issue with that.
That was tube (singular).
Don't be a clown with this red herring stuff, one might mistake you for an educated eejit. You pick the valve for the job and if need be put them in parallel as you subsequently added.
Sorry to offend. I didn't think I was being an idjit, but rather, adding something quantitative to the mix. Which … all in all … seems overly hopeful on my part. Oh well. ⋅-=≡ GoatGuy ✓ ≡=-⋅
- Home
- Amplifiers
- Tubes / Valves
- What's This Formula Tell You