Looking at all these threads on audio compensation, I can see that significant improvements in distortion can be made by combining local and global feedback and adding poles and zeros at particular places.
For the sake of argument, lets assume an amplifier is a linear device in the sense that the superposition principle applies: if the sum of two signals are applied to the input of an amplifier, the output should be the sum of the two signals that would be output from the amplifier from each of the two signals alone. This is of course not true due to distortion which is the whole point of such compensation schemes. But small-signal analysis is used to inform stability analysis which determines whether a given compensation scheme is likely to be stable and therefore a necessary (but not sufficient) condition for an amplifier to be useful for reducing distortion.
Many of these distortion compensation methods rely on taking the output and then applying a linear function of that output to various stages in the circuit. This could be modeled where the output voltage is scaled by a transfer function transconductance with amplitude/phase as function of frequency so that currents are injected into various points into the previous stages as to provide a feedback mechanism.
So I now pose the following problem. Let's say we start with a given amplifier circuit comprising and input and output with a single current source where the feedback is to be injected at a stage, and therefore with zero transconductance is nominally an open circuit and produces no modification to the amplifier output. Furthermore, lets say for this circuit we can expand the output voltage as a polynomial in the input voltage, so that at least for relatively low audio frequencies, the polynomial terms corresponding to the second-order distortion, third-order distortion, etc. can be identified.
Given, say, one wishes to minimize a particular distortion term, say third-order distortion, is there an ideal transconductance that achieves that? This would be finding the amplitude and phase of the transconductance transfer function that would minimize the distortion, for example, the third-order distortion. The transconductance would not necessarily be limited to what could be easily achieved by a few passive components, but for example, could be applied by using a DSP to calculate the feedback current from the output voltage using some FIR filter.
One could then, for example, describe an amplifier linear transfer function with the output being dependent on the input voltage and feedback current (from the transconductance) and therefore optimize the FIR filter and find the "ideal" compensation filter.
The idea then would be to extract the transfer function from a SPICE model, perform this optimization, and then include the filter in the SPICE model to see what improvement might result.
This may be overkill but it seems to me that there should be some optimal feedback filter in the sense of control theory.
For the sake of argument, lets assume an amplifier is a linear device in the sense that the superposition principle applies: if the sum of two signals are applied to the input of an amplifier, the output should be the sum of the two signals that would be output from the amplifier from each of the two signals alone. This is of course not true due to distortion which is the whole point of such compensation schemes. But small-signal analysis is used to inform stability analysis which determines whether a given compensation scheme is likely to be stable and therefore a necessary (but not sufficient) condition for an amplifier to be useful for reducing distortion.
Many of these distortion compensation methods rely on taking the output and then applying a linear function of that output to various stages in the circuit. This could be modeled where the output voltage is scaled by a transfer function transconductance with amplitude/phase as function of frequency so that currents are injected into various points into the previous stages as to provide a feedback mechanism.
So I now pose the following problem. Let's say we start with a given amplifier circuit comprising and input and output with a single current source where the feedback is to be injected at a stage, and therefore with zero transconductance is nominally an open circuit and produces no modification to the amplifier output. Furthermore, lets say for this circuit we can expand the output voltage as a polynomial in the input voltage, so that at least for relatively low audio frequencies, the polynomial terms corresponding to the second-order distortion, third-order distortion, etc. can be identified.
Given, say, one wishes to minimize a particular distortion term, say third-order distortion, is there an ideal transconductance that achieves that? This would be finding the amplitude and phase of the transconductance transfer function that would minimize the distortion, for example, the third-order distortion. The transconductance would not necessarily be limited to what could be easily achieved by a few passive components, but for example, could be applied by using a DSP to calculate the feedback current from the output voltage using some FIR filter.
One could then, for example, describe an amplifier linear transfer function with the output being dependent on the input voltage and feedback current (from the transconductance) and therefore optimize the FIR filter and find the "ideal" compensation filter.
The idea then would be to extract the transfer function from a SPICE model, perform this optimization, and then include the filter in the SPICE model to see what improvement might result.
This may be overkill but it seems to me that there should be some optimal feedback filter in the sense of control theory.
No.
There are very much different kinds of "distortion" and not all of them are easily sensible by simple simulation.
What about coupling between power trafo and amp's output coil?
What about nonlinear behaviour between common mode itself and common mode error?
What about long time thermal-related idle current and bias distortion?
Even what about input distortion caused by changing volume regulator resistanse?
Things become more and more complicated.
Let's start from something simple like avoiding noninverting amplifiers?
😉
Let me suppose - just for fun. All bicycles are already invented and now designers mostly check niceness or, if you wish, appreciate the beauty of the solution.
FIR is a good method for compensate time-related effects like roomgain and room resonances at low-freq or phase-aligning dedicated bands. But it is not related to all possible effects in a control system such an audio amp.
Being really, there are not so much peoples to talk about pole-zero related questions, or all complexity of the audio amlifier designing.
I have done many heavy numerical optimization problems, mostly in optical and electromagnetic design, and I was wondering if amplifier design could be framed in such a way. While there is a heavy element of garbage in-garbage out to such methods, they can produce remarkable and unexpected results that point the way to new ways to doing things.
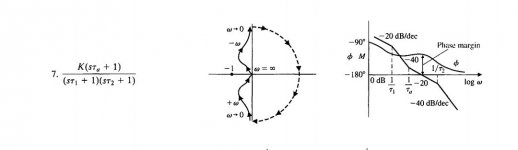
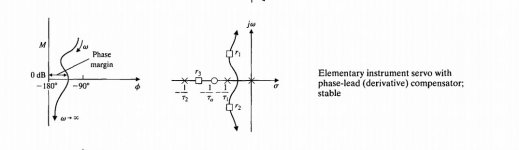
It's not clear to me whether you are thinking about negative feedback, distortion compensation or some hybrid method using both. Frequency compensation in a negative feedback amplifier is actually a misnomer, as it has very little to do with cancelling some undesired phenomenon with something that's equal but opposite. It just means tailoring the circuit such that it becomes stable.
Distortion compensation is sometimes used to, for example, get a more or less acceptable sound out of a much too small loudspeaker. Usually those are more or less open-loop methods: you have some fancy digital predistorting thing, then an amplifier and then the loudspeaker, but no path from the loudspeaker back into the predistorting thing (otherwise it would be motional feedback). I don't think anyone has ever applied it to audio amplifiers. Predistortion is used for RF amplifiers, though.
For negative feedback to be maximally effective, you normally just try to get as much loop gain as you can over the band of interest. The trick is to do so without making the circuit unstable.
Distortion compensation is sometimes used to, for example, get a more or less acceptable sound out of a much too small loudspeaker. Usually those are more or less open-loop methods: you have some fancy digital predistorting thing, then an amplifier and then the loudspeaker, but no path from the loudspeaker back into the predistorting thing (otherwise it would be motional feedback). I don't think anyone has ever applied it to audio amplifiers. Predistortion is used for RF amplifiers, though.
For negative feedback to be maximally effective, you normally just try to get as much loop gain as you can over the band of interest. The trick is to do so without making the circuit unstable.
profdc9, I recommend you obtain a copy of this paper. The authors use numerical optimization with constraints, to derive the optimum compensation for a composite amplifier -- a cascade of two high performance opamps -- which is a notoriously difficult problem. They succeeded quite grandly.
I've used numerical optimization myself in circuit design, in fact wrote my master's thesis on the topic ... in the bad old days before the c++ or python languages were created (thus the num.py library had not been written yet). I suspect the approach these authors took, will be of great interest to you.
AES Journal Volume 65 Issue 5, pp. 402-407
I've used numerical optimization myself in circuit design, in fact wrote my master's thesis on the topic ... in the bad old days before the c++ or python languages were created (thus the num.py library had not been written yet). I suspect the approach these authors took, will be of great interest to you.
AES Journal Volume 65 Issue 5, pp. 402-407
About 40 years ago, Ernst Nordholt came up with some simple heuristic rules. I don't remember exactly what he wrote, but it boiled down to something like:
1. Try to get the amplifier stable by just adding zeros
2. If 1 is insufficient or impossible, add local feedback loops that exchange overall loop gain for local loop gain over the frequency range where you need to reduce loop gain
3. If that doesn't work either, use brute-force methods that throw away overall loop gain without getting anything in return
By the way, you might be interested in the Ph.D. thesis of Hans Stoffels, Automation in high-performance negative feedback amplifier design | TU Delft Repositories
1. Try to get the amplifier stable by just adding zeros
2. If 1 is insufficient or impossible, add local feedback loops that exchange overall loop gain for local loop gain over the frequency range where you need to reduce loop gain
3. If that doesn't work either, use brute-force methods that throw away overall loop gain without getting anything in return
By the way, you might be interested in the Ph.D. thesis of Hans Stoffels, Automation in high-performance negative feedback amplifier design | TU Delft Repositories
Last edited:
It's free (and legal) here:
https://pdfs.semanticscholar.org/b96c/62efa54d464b7fbb7c5bf61906e3cbb9b830.pdf
Ok. This could be done more or less easy.
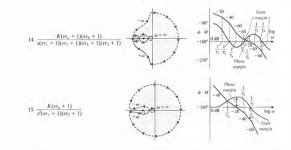
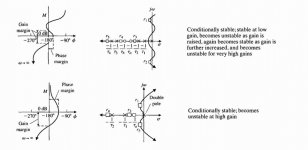
Dominant pole design have no optimisation criteria except bandwidth, so i have attached higher order plots.
Usually poles are defined by component selection - opamps, VAS stage capacitive load(which stabilizes small but deviating OPS input capacitance) or gain/freq ratio of the standalone transistor discrete stages.
There are some design goals for your choice:
1. As low as possible unity gain frequency
2. As low as possible additional components to PCB layout
3. As low as possible additional zeros to conditionally or unconditionally stabilize
4. As high as possible achieved gain at a given ULGF
5. As high as possible gain at a given freq (say 20 kHz for simplicity) with a fixed poles/zeros quantity.
So you will have some order relation with defined and undefined parameters and can easily use any choosed optimization method for choosed optimization criteria.
But, really, there are popular so simple amplifiers that, let me suppose, no such an optimization tasks was performed.
