No matter whether it is inductive, capacitive or resistive, when the source impedance is high, it doesn't short the termination resistor, does it?
You got me thinking...
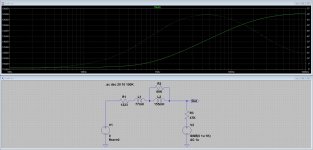
Here's a quick & dirty sim of an equivalent circuit as per Elliott. The moral is: you're half right above 1KHz, and I'm half right below. But since the RIAA EQ will filter the HF subsequently, the contribution of the inductances is negligible.
Here's a quick & dirty sim of an equivalent circuit as per Elliott. The moral is: you're half right above 1KHz, and I'm half right below. But since the RIAA EQ will filter the HF subsequently, the contribution of the inductances is negligible.
Attachments
Ever heard of psychoacoustic noise weighting? An A-weighting filter rolls off much faster below 1 kHz than a RIAA response increases. In the end, with RIAA- and A-weighting, it's the impedance around 3852 Hz that matters. With RIAA- and ITU-R 468 weighting, it's even a bit higher.
Last edited:
See the attachment for the derivation of that 3852 Hz. By taking the Norton equivalent of the termination resistor, that is, treating it as a noise current source in parallel with a resistor, you can see immediately that it contributes to i_n. It's 5179 Hz with RIAA and ITU-R 468 weighting.
Attachments
What's the equivalent input noise current of the measurement amplifier (including sqrt(4 k T/R) of the input resistor, if any)?
What's the equivalent input noise current of the measurement amplifier (including sqrt(4 k T/R) of the input resistor, if any)?
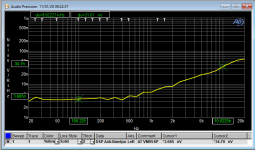
Just the LA article amplifier - not quite built to Sam's elegant design. Reality tested with 60 ohm and 10k ohm resistor.
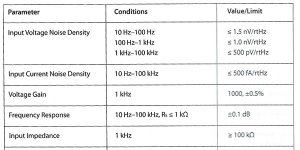
Here are some of the specs from the article:
Attachments
The noise goes as the square root of the resistance..
The step from 1kohm to 1Mohm is 30dB.
Oops somehow lost loads of responses..
The step from 1kohm to 1Mohm is 30dB.
Oops somehow lost loads of responses..
Assuming the magnitude of the impedance is close to the theoretical sqrt(R^2 + 4 pi^2 f^2 L^2):
500 fA/sqrt(Hz), 550 mH in series with 485 ohm and 10.0225 kHz boils down to 17.31933 nV/sqrt(Hz) of noise voltage due to the equivalent input noise current of the amplifier. You measure 34.7 nV/sqrt(Hz), so most of that, 30.07 nV/sqrt(Hz), must be real cartridge thermal noise.
The ESR at 10.0225 kHz is then about 55.8 kohm, which is more than the theoretical 34.6 kohm of impedance at 10.0225 kHz. Maybe it is getting too close to resonance with whatever capacitance it may have to assume that the magnitude of the impedance is close to the theoretical sqrt(R^2 + 4 pi^2 f^2 L^2). That also means that a larger part of the noise than just calculated may be due to the amplifier's input noise current. Besides, the input impedance of the amplifier may not be negligibly high anymore.
Doing a similar calculation with 13 nV/sqrt(Hz) at 3 kHz to hopefully stay well below resonance, I find a cartridge thermal noise of 11.919 nV/sqrt(Hz), an ESR of 8.7755 kohm and a theoretical impedance of 10.3786 kohm.
An acquaintance of mine once measured the impedance of a Shure V15-III and also found that the ESR increases a lot with frequency, as the phase angle never exceeded 72 degrees. Apparently your ATVM95_SP cartridge is even lossier than his V15-III.
500 fA/sqrt(Hz), 550 mH in series with 485 ohm and 10.0225 kHz boils down to 17.31933 nV/sqrt(Hz) of noise voltage due to the equivalent input noise current of the amplifier. You measure 34.7 nV/sqrt(Hz), so most of that, 30.07 nV/sqrt(Hz), must be real cartridge thermal noise.
The ESR at 10.0225 kHz is then about 55.8 kohm, which is more than the theoretical 34.6 kohm of impedance at 10.0225 kHz. Maybe it is getting too close to resonance with whatever capacitance it may have to assume that the magnitude of the impedance is close to the theoretical sqrt(R^2 + 4 pi^2 f^2 L^2). That also means that a larger part of the noise than just calculated may be due to the amplifier's input noise current. Besides, the input impedance of the amplifier may not be negligibly high anymore.
Doing a similar calculation with 13 nV/sqrt(Hz) at 3 kHz to hopefully stay well below resonance, I find a cartridge thermal noise of 11.919 nV/sqrt(Hz), an ESR of 8.7755 kohm and a theoretical impedance of 10.3786 kohm.
An acquaintance of mine once measured the impedance of a Shure V15-III and also found that the ESR increases a lot with frequency, as the phase angle never exceeded 72 degrees. Apparently your ATVM95_SP cartridge is even lossier than his V15-III.
By the way, that 3.685 nV/sqrt(Hz) low-frequency asymptote corresponds to a DC resistance of 838.77 ohm rather than 485 ohm.
As I said at some point, I'm not into anything extreme. I just didn't want to bother with those devices, if I would end up drowning the music in noise. From what I get from the last page I can even use the JFet's in a RIAA, as they are equally noisy as the LT1113 and that is good enough to me.
Thanks for your time ansering my question. It has been educational.
Thanks for your time ansering my question. It has been educational.
By the way, that 3.685 nV/sqrt(Hz) low-frequency asymptote corresponds to a DC resistance of 838.77 ohm rather than 485 ohm.
Amplifer is oscillating in the MHz region -- my bad! I hadn't experienced this before. Works fine with resistive input.
- Home
- Amplifiers
- Solid State
- What JFET should i choose for a preamp?