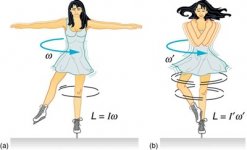
No.The work done by the skater in pulling in her arms results in an increase in rotational kinetic energy.
Increase in rotational speed.
Conservation of energy.
Approximately, because there is a bit of energy increase because of the skater effort to bring his arms to his body.
Talk about MOMENTUM!
In relation to your ice skater, you have to talk about conservation of angular momentum (L).
Linear momentum, p, is given by the product of mass (m) and velocity (v), and is conserved.
Angular momentum, L, is given bythe product of moment of inertia (I) and angular velocity (w), and is also conserved.
I'm pretty sure I explained the skater scenario to you earlier in the thread.
As the skater draws in her arms, her moment of inertia (the distribution of her mass around the axis of rotation) becomes smaller and so her angular velocity must increase in order to conserve the product, which is angular momentum.
Attachments
I'm hung up on additional energy requirement...
No... Conservation of energy.
I was at that point addressing Pete's particular reference to energy.
The full story lies, not with conservation of energy, but with conservation of angular momentum - as I have illustrated.
I often think that when one encounters an Obstacle in the Evolution of the Universe, one should take a break from it all .🙂
This Man claims to have solved the most Pressing Problem in Mathematics: The Riemann Hypothesis.
https://en.wikipedia.org/wiki/Riemann_hypothesis
TBH, I liked what I saw. 5040 and 7! an' all that.
Looks like a simple proof to me. But surely not that easy. Peer review will surely find a simple error.
This Man claims to have solved the most Pressing Problem in Mathematics: The Riemann Hypothesis.
https://en.wikipedia.org/wiki/Riemann_hypothesis
TBH, I liked what I saw. 5040 and 7! an' all that.
Looks like a simple proof to me. But surely not that easy. Peer review will surely find a simple error.
Attachments
...one should take a break from it all .🙂
My idea of a break is not pursuing the solutions to challenging mathematical hypotheses! 😱
Breaking news!
The W boson is more massive than theory predicts!
https://www.bbc.co.uk/news/science-environment-60993523
Just how "shocking" is this, Steve?
The W boson is more massive than theory predicts!
https://www.bbc.co.uk/news/science-environment-60993523
Just how "shocking" is this, Steve?
I told you that Quantum Mechanics is always throwing up Surprises! Why I love it.
https://www.bbc.co.uk/news/science-environment-60993523
The Mass of the W(0) Boson is being reviewed. 😱
https://www.bbc.co.uk/news/science-environment-60993523
The Mass of the W(0) Boson is being reviewed. 😱
The rotational energy of the skater is:I was at that point addressing Pete's particular reference to energy.
The full story lies, not with conservation of energy, but with conservation of angular momentum - as I have illustrated.
E = I omega² / 2 ( omega: speed in Radian per second )
With conservation of E, decreasing I, induces an omega increase.
It is interesting to see how the rotational kinetic energy of the skater changes when she pulls her arms in. Her initial rotational energy is
![\[{K}_{\text{Rot}}=\frac{1}{2}I{\omega }^{2},\] \[{K}_{\text{Rot}}=\frac{1}{2}I{\omega }^{2},\]](https://opentextbc.ca/universityphysicsv1openstax/wp-content/ql-cache/quicklatex.com-52315bff75d4b6cbff1bbdcdb6269750_l3.svg)
whereas her final rotational energy is
![\[{{K}^{\prime }}_{\text{Rot}}=\frac{1}{2}{I}^{\prime }{({\omega }^{\prime })}^{2}.\] \[{{K}^{\prime }}_{\text{Rot}}=\frac{1}{2}{I}^{\prime }{({\omega }^{\prime })}^{2}.\]](https://opentextbc.ca/universityphysicsv1openstax/wp-content/ql-cache/quicklatex.com-cf0c6570f2ae979ba3147eba3b4930d0_l3.svg)
Since
![\[{I}^{\prime }{\omega }^{\prime }=I\omega ,\] \[{I}^{\prime }{\omega }^{\prime }=I\omega ,\]](https://opentextbc.ca/universityphysicsv1openstax/wp-content/ql-cache/quicklatex.com-2c75a1c27d3e194ac2d61523facd9059_l3.svg)
we can substitute for
![\[{\omega }^{\prime }\] \[{\omega }^{\prime }\]](https://opentextbc.ca/universityphysicsv1openstax/wp-content/ql-cache/quicklatex.com-56cdbf22aff5201204ff71601af1ecc3_l3.svg)
and find
![\[{{K}^{\prime }}_{\text{Rot}}=\frac{1}{2}{I}^{\prime }{({\omega }^{\prime })}^{2}=\frac{1}{2}{I}^{\prime }{(\frac{I}{{I}^{\prime }}\omega )}^{2}=\frac{1}{2}I{\omega }^{2}(\frac{I}{{I}^{\prime }})={K}_{\text{Rot}}(\frac{I}{{I}^{\prime }})\text{}.\] \[{{K}^{\prime }}_{\text{Rot}}=\frac{1}{2}{I}^{\prime }{({\omega }^{\prime })}^{2}=\frac{1}{2}{I}^{\prime }{(\frac{I}{{I}^{\prime }}\omega )}^{2}=\frac{1}{2}I{\omega }^{2}(\frac{I}{{I}^{\prime }})={K}_{\text{Rot}}(\frac{I}{{I}^{\prime }})\text{}.\]](https://opentextbc.ca/universityphysicsv1openstax/wp-content/ql-cache/quicklatex.com-e13a45dabcb01b20e985b90371c86bd7_l3.svg)
Because her moment of inertia has decreased,
![\[{I}^{\prime }<I,\] \[{I}^{\prime }<I,\]](https://opentextbc.ca/universityphysicsv1openstax/wp-content/ql-cache/quicklatex.com-ac315b471ae3bcd0255f88ffeaeb1545_l3.svg)
her final rotational kinetic energy has increased. The source of this additional rotational kinetic energy is the work required to pull her arms inward.
This work causes an increase in the rotational kinetic energy, while her angular momentum remains constant.
Since she is in a frictionless environment, no energy escapes the system. Thus, if she were to extend her arms to their original positions, she would rotate at her original angular velocity and her kinetic energy would return to its original value.
Copied from here: https://opentextbc.ca/universityphysicsv1openstax/chapter/11-2-conservation-of-angular-momentum/
whereas her final rotational energy is
Since
we can substitute for
and find
Because her moment of inertia has decreased,
her final rotational kinetic energy has increased. The source of this additional rotational kinetic energy is the work required to pull her arms inward.
This work causes an increase in the rotational kinetic energy, while her angular momentum remains constant.
Since she is in a frictionless environment, no energy escapes the system. Thus, if she were to extend her arms to their original positions, she would rotate at her original angular velocity and her kinetic energy would return to its original value.
Copied from here: https://opentextbc.ca/universityphysicsv1openstax/chapter/11-2-conservation-of-angular-momentum/
I dong recall saying any of the inertial frames of reference were not valid. Just that if I accelerate an object, I’m shifting its inertial frame of reference from what it was previously to a new inertial frame of reference.Any frame of reference in which Newton 1 is valid is an inertial frame.
In what way can an inertial frame change according to the above definition?
I dong recall saying any of the inertial frames of reference were not valid.
Nor did I say that.
I said Newton 1 had to be valid for it to be an inertial reference frame.
I'm still not sure what makes one inertial frame different from another.
I can't believe it! The angular momentum of reprocessing my order for that True mirror due to it's "undeliverable" status(assume they broke it), has resulted in a second round of re-rder now expected this Saturday(assume someone now stole it...Prime Member status). There were 3 available, all of which are now in question. If this last one goes missing I'll have to take drastic measures and feel my face like a blind person to discover the difference! Good thing there's the required admiration as Einstein mentions for science to affirm itself, eh! 💋
Last edited:
When you move something from point A to point B, you accelerate it which simply means you are shifting its inertial frame. Once you remove the force (cease energy expenditure), it occupies a new inertial frame...
Let's revisit your original statement, Bonsai.
Obviously it is quite permissable for an object to accelerate within an inertial frame (since Newton's second law applies there), but during the acceleration why wouldn't the object stay within that same inertial frame?
Once the accelerating force is removed the object continues to move within the same inertial frame - surely it doesn't now occupy a new inertial frame?
True mirror
I've no idea what you are talking about, and I'm not going to google it as I am not a happy bunny!
Your lack of positive feedback to my discussions on the ice skater scenario you introduced dissuades me from answering any more of your questions.
Communication is a two-way process you know.
Sometimes we all need to look in the mirror!
Isn't inertial frame subject to change via acceleration? If kinetic energy is increased, does this not translate to a different inertial frame of reference?but during the acceleration why wouldn't the object stay within that same inertial frame?
Huh?I've no idea what you are talking about, and I'm not going to google it as I am not a happy bunny!
Your lack of positive feedback to my discussions on the ice skater scenario you introduced dissuades me from answering any more of your questions.
Communication is a two-way process you know.
Sometimes we all need to look in the mirror!
okay,..sure
it's weird that it took you a half hour to lash out..with a response to Bonsai in between.🤪
Last edited:
CORRECT!As the skater draws in her arms, her moment of inertia (the distribution of her mass around the axis of rotation) becomes smaller and so her angular velocity must increase in order to conserve the product, which is angular momentum.
thank you very much, spoken very quickly! 😎
expanding space doesn't expand field effective area . Ie. It's cannot make field strong or week . And light is made up of oscillating magnetic and electric fields . Therefore the speed of light is un effected by the fact universe is expanding.
Rate of expansion is not constant . It's higher in voids . Decent intergalactic space . Small in galaxy . And minimal inside black hole . That's what I think . Expansion is hindered by
If an object or objects are coasting through space their IFOR doesn’t change. I used the example of two objects which then had a force acting on one or both. So the IFOR’s between them changed.Let's revisit your original statement, Bonsai.
Obviously it is quite permissable for an object to accelerate within an inertial frame (since Newton's second law applies there), but during the acceleration why wouldn't the object stay within that same inertial frame?
Once the accelerating force is removed the object continues to move within the same inertial frame - surely it doesn't now occupy a new inertial frame?
- Status
- Not open for further replies.
- Home
- Member Areas
- The Lounge
- What is the Universe expanding into..