All this talk of death is deeply depressing. Time to lighten up and get back to Maths and Physics! 😀

Rockall is a tiny Island infested with fishy birds called Puffins, AFAIK. And not much else. Nominally owned by Dear Old Blighty, but so far not tested in the Courts. Reason it matters is it extends British fishing rights far out into the Atlantic. Possession is 9/10 of the Law.
My favourite Mathematical Island is that of the Prime Numbers. Good item at Quanta this week. The Riemann Hypothesis. Quanta Magazine
All our old mathematical favourites involved. Euler, Gauss and Bernhard Riemann. I have always been entranced by the Zeta function. Pi ^2 /6 and all that. Broken for odd values. I thought the zeroes were on the minus half line, but seems they are on the plus half line. Nevertheless, I think somebody, one day, shall prove the Riemann Hypothesis. 😎

Rockall is a tiny Island infested with fishy birds called Puffins, AFAIK. And not much else. Nominally owned by Dear Old Blighty, but so far not tested in the Courts. Reason it matters is it extends British fishing rights far out into the Atlantic. Possession is 9/10 of the Law.
My favourite Mathematical Island is that of the Prime Numbers. Good item at Quanta this week. The Riemann Hypothesis. Quanta Magazine
All our old mathematical favourites involved. Euler, Gauss and Bernhard Riemann. I have always been entranced by the Zeta function. Pi ^2 /6 and all that. Broken for odd values. I thought the zeroes were on the minus half line, but seems they are on the plus half line. Nevertheless, I think somebody, one day, shall prove the Riemann Hypothesis. 😎
But preferably where they apply to cosmology and not simply for academic purposes!All this talk of death is deeply depressing. Time to lighten up and get back to Maths and Physics! 😀
I think somebody, one day, shall prove the Riemann Hypothesis.
What's that got to do with the price of bread?! 😕In mathematics, the Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 12. ... It has zeros at the negative even integers; that is, ζ(s) = 0 when s is one of −2, −4, −6, .... These are called its trivial zeros.
I think the water current patterns around the island reminded Steve of Riemann......could be ADD as well? 😀
IMO, it won't be the Physicists who solve the Universe, it will be the Mathematicians. 😱
Gauss had an illustrious record as an Astronomer. He managed to rediscover the largest minor planet Ceres:
Ceres (dwarf planet) - Wikipedia
First glimpsed in 1801, it went missing! To lose a minor planet wreaks of carelessness. Gauss calculated where it had gone, and it was rediscovered. 😎
Euler, another guy who spent time calculating the moon discovered the Beta, Zeta and Gamma functions. Now considered essential to String Theory
Leonhard Euler - Wikipedia
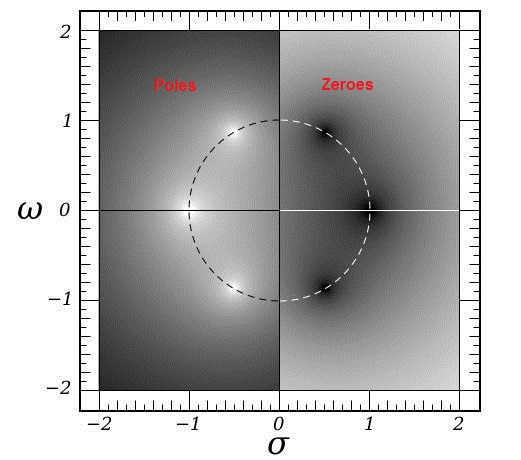
Believe me, complex poles and zeroes and primes have a great deal to do with Cosmology.
Just we are a bit too thick to figure it out. 😱
Gauss had an illustrious record as an Astronomer. He managed to rediscover the largest minor planet Ceres:
Ceres (dwarf planet) - Wikipedia
First glimpsed in 1801, it went missing! To lose a minor planet wreaks of carelessness. Gauss calculated where it had gone, and it was rediscovered. 😎
Euler, another guy who spent time calculating the moon discovered the Beta, Zeta and Gamma functions. Now considered essential to String Theory
Leonhard Euler - Wikipedia
The vertex operators were analytically continued into the complex plane by Mandelstam, who reinterpreted the string scattering as a 2-d quantum field theory on the worldsheet. Many people converted this scattering amplitude into a consistent S-matrix for scattering of open and closed strings both, but it requires a lot of physical insight, because the Euler beta function is just a simplest case of scattering, and you need to relate the scattering to more comprehensible physics, and the string picture introduced by Ramond, Susskind, Nielson, and Nambu was essential for this.
But the original idea was a phenomenological way to get scattering with integer spaced poles on straight lines, and this is what started string theory. Gamma function fits were done all the time in the 1960s, after Chew and Frautschi showed that the straight-line Regge trajectories described the known mesons, and this was verified as new mesons were discovered.
Believe me, complex poles and zeroes and primes have a great deal to do with Cosmology.
Just we are a bit too thick to figure it out. 😱
Tranquility Base
It's now the law that the historic sites where humans first landed on the Moon must be protected.
New law is first to protect Apollo sites from future moon missions | collectSPACE
It's now the law that the historic sites where humans first landed on the Moon must be protected.
New law is first to protect Apollo sites from future moon missions | collectSPACE
Attachments
Oh don't make me swoop in sideways eh!
OTOH, science be the judge, why pray tell is there no blast crater under that magnificent monstrosity?
OTOH, science be the judge, why pray tell is there no blast crater under that magnificent monstrosity?
Last edited:
In cosmology, their approach differs, but both study the mathematical apparatus of physical theories.IMO, it won't be the Physicists who solve the Universe, it will be the Mathematicians. 😱
In a nutshell, mathematical physicists develop mathematics and theoretical physicists develop theories! 😎A mathematical physicist is interested in the logical consequences of postulates, a theoretical physicist is interested in making predictions for and explanations of experimental results.
The lunar module descent engine at 25% throttle is about the same as the taxi thrust (5%) of a 737, the amount of thrust used to get the aircraft moving after it has pushed back from the gate. You don't see it throwing baggage carts or workers across the ramp. It is hard to imagine it digging down to bedrock. Clavius: Vehicles - the blast crater...why pray tell is there no blast crater under that magnificent monstrosity?
Applications Of Conformal Geometric Algebra To Transmission Line Theory
I never learned transmission line theory or Smith Chart but this presentation of the IEEE paper's Geometric Algebra was fun to for me:
Applications Of Conformal Geometric Algebra To Transmission Line Theory - YouTube
builds Riemann Sphere projective model of Smith Chart then goes up to Minkowski Space to turn all S-Chart transformations into Lorentz Transforms/Rotations
Geometric Algebra links:
Geometric Algebra: A collection of useful resources []
I never learned transmission line theory or Smith Chart but this presentation of the IEEE paper's Geometric Algebra was fun to for me:
Applications Of Conformal Geometric Algebra To Transmission Line Theory - YouTube
builds Riemann Sphere projective model of Smith Chart then goes up to Minkowski Space to turn all S-Chart transformations into Lorentz Transforms/Rotations
Geometric Algebra links:
Geometric Algebra: A collection of useful resources []
Whoa!!!, eeeasy tiguan. How about a mere disturbance?The lunar module descent engine at 25% throttle is about the same as the taxi thrust (5%) of a 737, the amount of thrust used to get the aircraft moving after it has pushed back from the gate. You don't see it throwing baggage carts or workers across the ramp. It is hard to imagine it digging down to bedrock. Clavius: Vehicles - the blast crater
That's your idea of fun?! 😱...this presentation of the IEEE paper's Geometric Algebra was fun to for me
You and Steve are going to get on like a house on fire! 😀
There are signs of sooting and the erosion pattern from the exhaust can be clearly seen in a higher resolution image than the one attached. The area directly beneath the nozzle, which would have been subjected to the most heat, is discoloured slightly red.How about a mere disturbance?

Unfortunately, this is what we expect to see under the lunar module. The exhaust plume is simply not powerful enough to dig holes in the tightly-packed regolith. Clavius: Vehicles - the blast crater
Attachments
I'm not that far along mathematically, my slight ambition is to get to a "Space Time Algebra" understanding of Electromagnetism
Complex numbers have been helpful in Linear Control theory, the following was more my former professional speed:
Complex numbers have been helpful in Linear Control theory, the following was more my former professional speed:
Originally posted by jcx
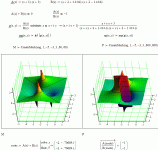
you could take a geometric pole/zero view
separate and then divide through to get
A(s)/B(s) = -1
then you could plot the | A(s)/B(s) | = 1 contours
and the Arg( A(s)/B(s) ) = pi isolines
their intersections are the roots of the summed polynomials, less the common roots which cancel in the division - of course the common roots are roots of the final sum too
computation wize this may not be a win but it should help in visualizing the relation of the roots of the sum to the starting polynomial's individual roots
there are likely lots of conformal mapping/complex analysis ideas that come in to play that I've mostly never learned or forgot

here I followed the above concept, but plotted ln(|g(s)|) - the poles and zeroes are more equally weighted by the log display, the ln(*) = 0 is of course the |*|= 1 locus, which is the hyperbolic appearing black contour line in the 1st plot
the phase surface is harder to interpret, there is a discontinuity where the arg function wraps from +pi to - pi, the intersections of these "tears" in the phase sheet with the 0 ln(magnitude) locus in the 1st plot are the locations of the roots of the sum of the polynomials
the phase wrap discontinuities connect poles with zeros in a conjugate symmetry preserving (minimal? ) set of phase isolines, this shows how the roots of the summed polynomial will be constrained to be "between" the pairs of roots of the A(s), B(s) starting polynomials
when the degree of A(s), B(s) are not equal, the "excess" poles or zeros in the ratio plot will be paired to the zeros or poles at infinity and be "connected" by a +/-pi phase wrap line to the paired infinity points, this indicates that "excess" roots in either A(s) or B(s) will be pushed away from the region of paired roots
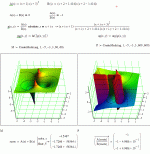
2nd pic:

this illustrates the pushing away of an "excess" root in A(s) vs the degree of B(s) - everything in the same positions/scale as the 1st plot, but the A(s) root (s+3) is squared giving a double zero in the A(s)/B(s) pole-zero surface
i think you can see the phase discontinuity ridge from the excess (s+3) heading out to its "paired" pole at -infinity on the left of the phase plot
numerically we now have a root at -4.5 in the summed polynomial which is "outside" of the region containing the A(s), B(s) roots
Attachments
Huh, have you seen the prints from their boots?? Signs of sooting?? Please. The actual response of the NASA scientists(I saw and heard it with my own better than now ears) was that the reason for no blast crater is because, and I quote, " they swooped in sideways and set down".
You're the only one digging a hole here, Pete. 😉The actual response of the NASA scientists . . . was that the reason for no blast crater is because, and I quote, " they swooped in sideways and set down".
Until the very last few seconds, the approach profile for the lunar module called for some forward motion. The exhaust probably wasn't focused on any one spot for very long.
Go pick a hole in jcx's 'Space Time Algebra'. 😀
Sure, whatever. It was a long time ago right?
like before the enabling technology. Still not there.
btw, you skipped over the footprints. No need to disturb them eh.🙂
like before the enabling technology. Still not there.
btw, you skipped over the footprints. No need to disturb them eh.🙂
Knockout bit of Maths from jcx there:

I am impressed. 🙂
Everything I love in Maths. 1.414 = Root 2 for a start. Not too sure about the lower numbers. Bit unfamiliar.
A bit of wormhole geometry thrown in. I have vague theories about wormholes.
But am frankly too thick to keep up with it all. I know my limits. 😀
I am impressed. 🙂
Everything I love in Maths. 1.414 = Root 2 for a start. Not too sure about the lower numbers. Bit unfamiliar.
A bit of wormhole geometry thrown in. I have vague theories about wormholes.
But am frankly too thick to keep up with it all. I know my limits. 😀
You don't seem to understand the rules of the game, Pete. 😉Sure, whatever. It was a long time ago right?
like before the enabling technology. Still not there.
I've given you some scientific reasons why there is no blast crater.
Now you have to give me some scientific reasons why there should be a blast crater.
- Status
- Not open for further replies.
- Home
- Member Areas
- The Lounge
- What is the Universe expanding into..