Isn't the question about the algorithm used?The simulation set-up of Hans can read in a .dsf file and calculate an FFT using LTSpice, if I understand it correctly.
To calculate a DFT directly from a DSD stream, wouldn't that require cross-correlation of sine and cosine waves with the DSD stream of 1-bit samples? It would presumably be a form of averaging, seems like anyway. (where a 1 is taken as a +1 sample, and a 0 is taken as a -1 sample, or something equivalent to that?)
Last edited:
The ADC and DAC have separate voltage references, so they will drift a bit with respect to each other when the temperature changes. How would that cause pumping?
It would not. But (if say) the regulator employed a complex AC/DC feedback scheme with peaking at sub-hz frequencies... (and yes, I did that and found out)...
Well, I'll be thunderstruck.
That's correct: the order is typically around five and any normal single-loop sigma-delta modulator of order greater than two is conditionally stable in the control-theoretical sense: reduce its loop gain too much without changing the loop's poles and zeros and it will oscillate. That's true no matter whether the loop filter is analogue or digital.
Why is this relevant?
I am trying to determine our confidence level that our digital domain modulators do not have some weird sub-Hz oscillation. I had some interesting experiences with sub Hz loop instability (in the analogue age) involving VERY large and VERY hot industrial plant machinery, which seared itself literally into both retina and memory. So I guess burned children and all that.
For PCM2DSD v4, my hypothesis was that there is some extremely small digital offset left, leading to split peaks with a distance well below the resolution bandwidth of the measurement. It sounded plausible until v3 and PWM8 also turned out to have varying distortion levels.
Well, we can only state that the system composed of Modulator(PCM2DSDV3, PCM2DSDV4, PWM8), DAC(RTZ) and ADC(suffusion of yellow) have what appears in an FFT to be varying distortion levels and unexpected distortion (I presume - as this unexpected distortion send us on this collective snark hunt and ALL THE WAY down the rabbit hole....
I can and have simulated the spectrum of PWM8 in the digital domain. I can run it longer and do DFTs on several parts of the output waveform.
Mind you, the SRC4392 asynchronous sample rate converter that I use and the interpolation chain are not included. The SRC4392 definitely has something with large time constants on board, namely the sample frequency ratio estimator.
Besides, I usually haven't included the dithered integer arithmetic used in the FPGA code, but rather extended wordlength floating point numbers - except for the quantizer output, of course.
Reminder to self, all simulation is only as good as the models are complete... As models are never complete, selecting what to omit is a minefield.
The simulation set-up of Hans can read in a .dsf file and calculate an FFT using LTSpice, if I understand it correctly.
Splendid, Does anyone with PWM8 and PCM2DSD hardware also happen to have a sufficiently fast logic analyser to record the output?
Thor
Isn't the question about the algorithm used?
To calculate a DFT directly from a DSD stream, wouldn't that require cross-correlation of sine and cosine waves with the DSD stream of 1-bit samples? It would presumably be a form of averaging, seems like anyway. (where a 1 is taken as a +1 sample, and a 0 is taken as a -1 sample, or something equivalent to that?)
Yes. You can also interpret it as 0 and 1, then you get a big DC peak.
Basically, a sigma-delta modulate is just a PCM signal with a rather short wordlength and a funny noise spectrum. Calculating its DFT is not different from doing the same with an ordinary PCM signal.
Yes. These measurements were made with my own ES9822PRO based ADC.
Ok, my bad. I must have missed that bit.
I guess given that Pjotr25 also noticed pumping, we can exclude the ADC, unless you both use the same one.
Thor
@ThorstenL I have a Saleae logic analyzer which is good for signals up to 50MHz or so, but no PWM8.
Don't know if Bohrok2610 can loopback a DSD stream or not. IIUC he did his own USB device implementation using STM32?
Don't know if Bohrok2610 can loopback a DSD stream or not. IIUC he did his own USB device implementation using STM32?
Last edited:
The DSD stream is a real and not a complex signal, treating it as compex doesn’t add anything since the phase is zero.Isn't the question about the algorithm used?
To calculate a DFT directly from a DSD stream, wouldn't that require cross-correlation of sine and cosine waves with the DSD stream of 1-bit samples? It would presumably be a form of averaging, seems like anyway. (where a 1 is taken as a +1 sample, and a 0 is taken as a -1 sample, or something equivalent to that?)
Multiplying it with sines and cosines happens within the DFT/FFT, that’s why you get a complex output.
With a real input this will result in a complex conjugate output.
There is only one Fourier algorithm, nothing to choose from. But what is shown in most cases are just the moduli of the positive transformation halve, where phase information is no longer available.
But that’s no part of the Fourier algorithm.
Hans
Who treated the DSD stream as complex? Not me.The DSD stream is a real and not a complex signal, treating it as compex doesn’t add anything since the phase is zero.
I was talking about the internal processing going on inside a DFT. One description of the ways to do it: https://www.dspguide.com/ch8/6.htm
It can be done graphically too. Please see attachment for one graphical approach.
In the end though, it all amounts to the same thing since it all performs a DFT on a real dataset.
Attachments
Last edited:
Sorry, that’s what I misunderstood from your suggestion to multiply the DSD stream with sines and cosines before doing the DFT.Who treated the DSD stream as complex? Not me.
But luckily we do agree that there is only one Fourier algorithm that can be executed through different steps, but all with the same output 😊
Hans
It wasn't before the DFT, it was the beginning of a DFT....suggestion to multiply the DSD stream with sines and cosines before doing the DFT.
"DFT is just correlation of digital signal x[n] with sine wave oscillating at frequency ωm"
https://erickson.academic.wlu.edu/files/courses2020/sigproc_s2020/readings/DFT_Intro.pdf
Also its important to recall that a DFT can be calculated for a single sine wave, or single cosine wave. It doesn't have to be a full blown FFT that calculates for all possible discrete sine and cosine waves at once.
Last edited:
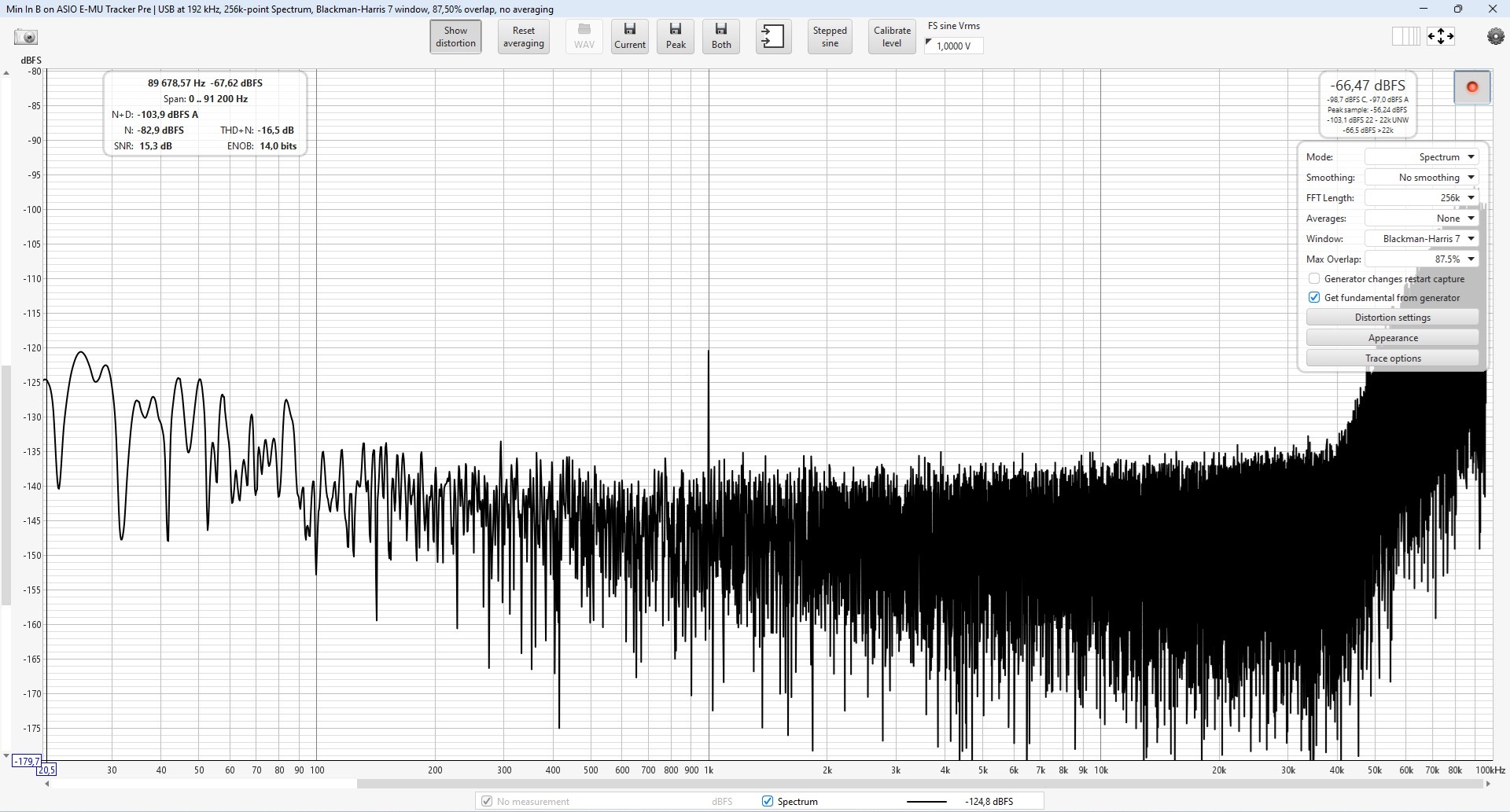
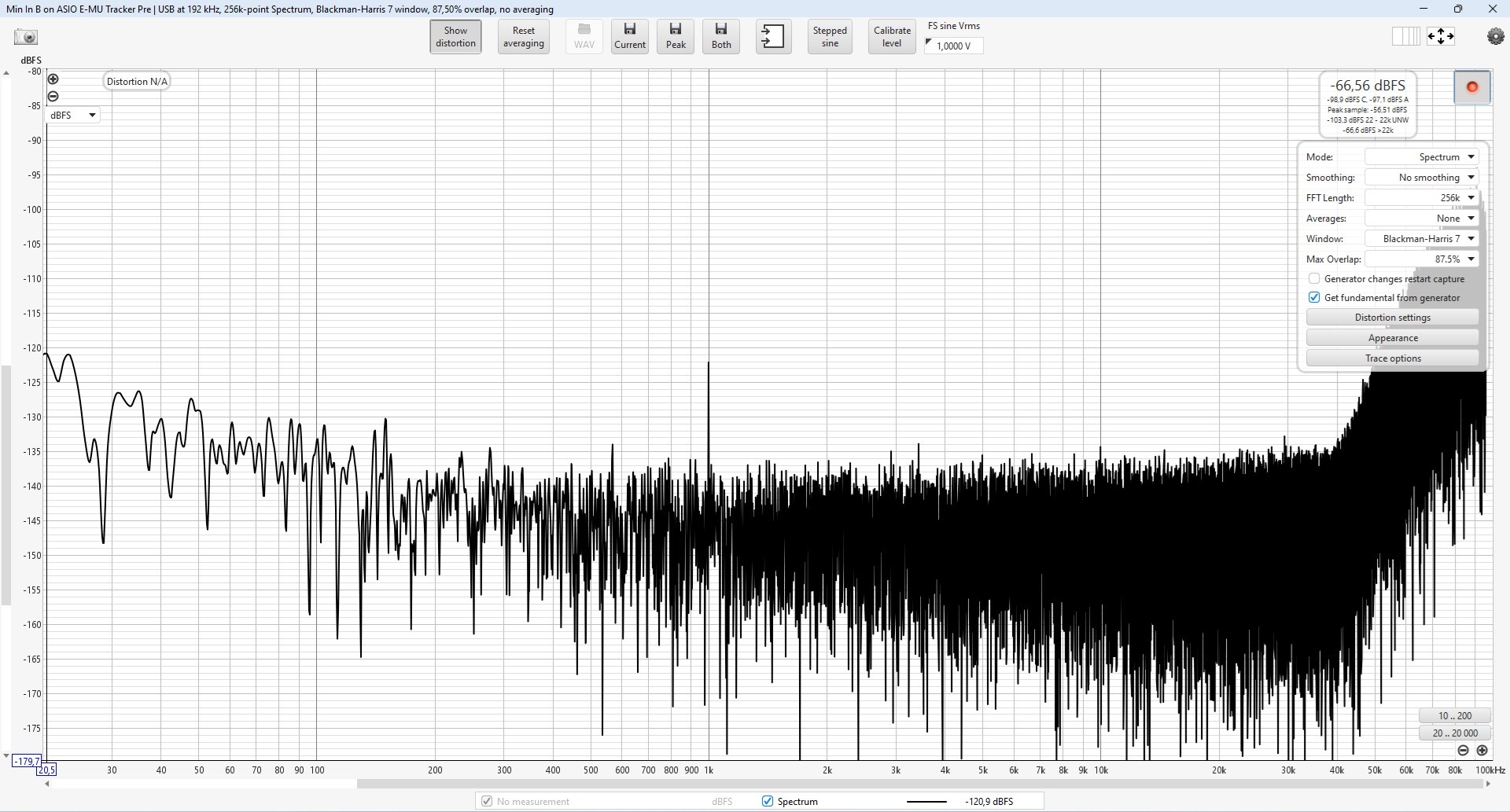
We are talking about harmonic pumping, but it's not just about harmonics...
I did a test for low levels of the carrier frequency
When we set the carrier low to around -100dBfs and below we can see carrier frequency pumping.
The lower the level, the more visible it is.
But I think that's we see it only. This is not real pumping.
It rather results from the way of the measurements.
These are simple measurements on simple equipment for signals at noise level.
When I look at the specifications of my measurement card I have: THD+N is about -100dB. This agrees with my measurements.
From this level I have pumping.
To see below -100dBfs we do various tricks.
We do averaging and select various parameters
Each sweep gives a different levels.
PWM8 -120dBfs:
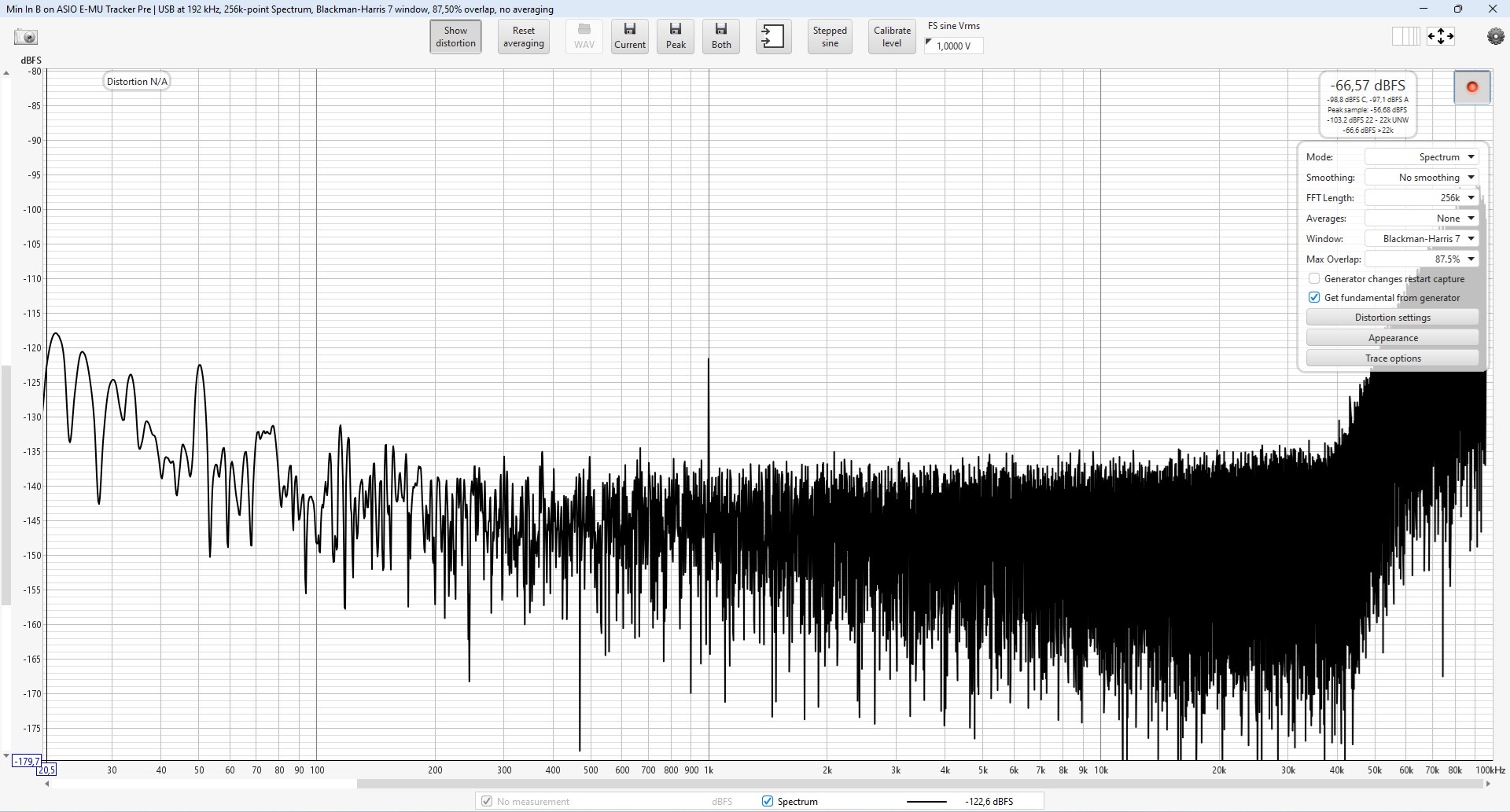
I did a test for low levels of the carrier frequency
When we set the carrier low to around -100dBfs and below we can see carrier frequency pumping.
The lower the level, the more visible it is.
But I think that's we see it only. This is not real pumping.
It rather results from the way of the measurements.
These are simple measurements on simple equipment for signals at noise level.
When I look at the specifications of my measurement card I have: THD+N is about -100dB. This agrees with my measurements.
From this level I have pumping.
To see below -100dBfs we do various tricks.
We do averaging and select various parameters
Each sweep gives a different levels.
PWM8 -120dBfs:
Good point, you always see some random level variations when the signal under test is too close to the noise floor. Sometimes the noise in the DFT bin or spectrum analyser resolution bandwidth is in phase with the signal, sometimes in antiphase, sometimes something in between.
Some kind of aliasing effect, like wagon wheels moving backwards in movies? And, or maybe a signal riding up and down on noise? Was wondering if it was real or not.
Not to be nitpicky but just to clarify, fs in lower case letters commonly refers to the sampling frequency (or sometimes f(s) is used instead). Whereas in the case of something like "-100dBFS," the FS in caps refers to "Full Scale," such as in the full scale output of a dac before it clips....around -100dBfs..
Sorry for the digression.
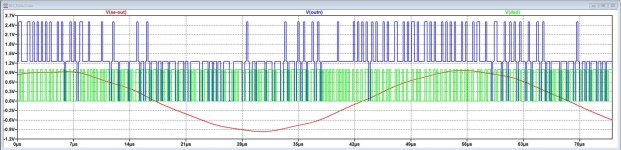
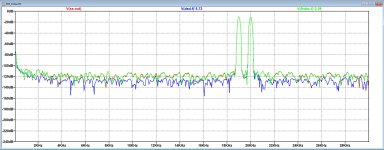
To show that the FFT of the DSD is no problem in LTSpice, here are 3 attachments taken while playing a 19+20Khz .dsf at -3dB peak.
The input DSD signal in the simulation switches between exactly 0 and 1Volt.
1) First attachment with a 75usec window of the DSD signal in Green, the Firdac's output without load in Blue and finally the filter output in Red are showing how much filtering takes place at each step.
2) Second attachment from a 16msec window shows a 500Mhz FFT with the DSD signal in Blue, the unloaded Firdac's output in Green and the SE filter output in Red.
To prevent folding into the audio spectrum, a simple 1K+10pF RC filter has been added after the DSD signal and also after the unloaded Firdac signal.
Signals are level adjusted in the FFT.
3) From this spectrum, a linear part has been zoomed in from 0 to 30Khz.
Obvious in this case is that the Firdac's signal and the SE Filter output are identical and exactly on top of each other.
However the DSD signal is ca. 10dB lower, so these 10dB must be lost somewhere in the digital processing part.
Hans
The input DSD signal in the simulation switches between exactly 0 and 1Volt.
1) First attachment with a 75usec window of the DSD signal in Green, the Firdac's output without load in Blue and finally the filter output in Red are showing how much filtering takes place at each step.
2) Second attachment from a 16msec window shows a 500Mhz FFT with the DSD signal in Blue, the unloaded Firdac's output in Green and the SE filter output in Red.
To prevent folding into the audio spectrum, a simple 1K+10pF RC filter has been added after the DSD signal and also after the unloaded Firdac signal.
Signals are level adjusted in the FFT.
3) From this spectrum, a linear part has been zoomed in from 0 to 30Khz.
Obvious in this case is that the Firdac's signal and the SE Filter output are identical and exactly on top of each other.
However the DSD signal is ca. 10dB lower, so these 10dB must be lost somewhere in the digital processing part.
Hans
Attachments
As I spend almost all my time at work behind a simulator, I really don't like doing simulations at home as well, so I'm building a prototype for my discrete filter on perfboard. One channel is ready, but it behaves as a common-mode oscillator so far.
Assuming I can get it stable and that I make a (SMD) version with a decent PCB, it is still very doubtful whether it will have any performance advantages at all compared to bohrok2610's latest filters. Still, it is fun to make it.
To be continued...

Assuming I can get it stable and that I make a (SMD) version with a decent PCB, it is still very doubtful whether it will have any performance advantages at all compared to bohrok2610's latest filters. Still, it is fun to make it.
To be continued...
Last edited:
Looking forward to seeing this Marcel , it’s nice having options to try with your FIRDAC . It’s always interesting to see how well a discrete option compares against op-amps
A bit surprised that I lost 10dB along the line from DSD input to Filter output, I found out that this was caused by the unloaded additional tap on the Firdac.To show that the FFT of the DSD is no problem in LTSpice, here are 3 attachments taken while playing a 19+20Khz .dsf at -3dB peak.
The input DSD signal in the simulation switches between exactly 0 and 1Volt.
1) First attachment with a 75usec window of the DSD signal in Green, the Firdac's output without load in Blue and finally the filter output in Red are showing how much filtering takes place at each step.
2) Second attachment from a 16msec window shows a 500Mhz FFT with the DSD signal in Blue, the unloaded Firdac's output in Green and the SE filter output in Red.
To prevent folding into the audio spectrum, a simple 1K+10pF RC filter has been added after the DSD signal and also after the unloaded Firdac signal.
Signals are level adjusted in the FFT.
3) From this spectrum, a linear part has been zoomed in from 0 to 30Khz.
Obvious in this case is that the Firdac's signal and the SE Filter output are identical and exactly on top of each other.
However the DSD signal is ca. 10dB lower, so these 10dB must be lost somewhere in the digital processing part.
Hans
Without this extra tap there is no loss and noise before and after stays at the same -130dB.
Hans
Marcel,As I spend almost all my time at work behind a simulator, I really don't like doing simulations at home as well, so I'm building a prototype for my discrete filter on perfboard. One channel is ready, but it behaves as a common-mode oscillator so far.
Assuming I can get it stable and that I make a (SMD) version with a decent PCB, it is still very doubtful whether it will have any performance advantages at all compared to bohrok2610's latest filters. Still, it is fun to make it.
To be continued...
View attachment 1312471
I think the pink things near the top are inductors.
If so, you may find this type to materially raise HD.
May I suggest you use the kind I used in the iDSD Pro for iFi AND that you pass a few mA DC current to "bias" the core?
Thor
- Home
- Source & Line
- Digital Line Level
- Return-to-zero shift register FIRDAC