At some very low frequency where the wavelength of the sound being reproduced by a closed- back (sealed) loudspeaker system is much greater than the dimensions of the speaker box, the sound pressure level (SPL) measured behind and in front of the speaker system is the same. That is, the difference of SPL readings front and back equals 0 dB. My question is, if frequency is increased to be equal to the baffle step frequency of the speaker system, what then is the difference of SPL readings front and back?
Please don't ask me why I want to know this; I have my reasons which I would rather not bring into the discussion for now anyway. Just think of it as a challenge to your understanding of the acoustics of closed-box loudspeaker systems.
This is a question excluding the open baffle or dipole type of speaker system.
Regards,
Pete
Please don't ask me why I want to know this; I have my reasons which I would rather not bring into the discussion for now anyway. Just think of it as a challenge to your understanding of the acoustics of closed-box loudspeaker systems.
This is a question excluding the open baffle or dipole type of speaker system.
Regards,
Pete
Last edited:
Actually, it would NOT apply to various different types of speakers. Many types do not exhibit a baffle diffraction step.
Regardless, there are myriad references to this. Here's just one:
http://www.t-linespeakers.org/tech/bafflestep/index.html
Dave.
Regardless, there are myriad references to this. Here's just one:
http://www.t-linespeakers.org/tech/bafflestep/index.html
Dave.
Yes, thank you, I realized what you write a few minutes after I had made the post. My post has been edited to reflect that.
Wavelength is the key, baffle width second, depth and shape of the box is far less important. There are many other factors as well, eg. driver diameter, interferences and resonances.
I am illiterate in maths, but I like to look at pictures, like a child!
Check these measured results as spectrograms. Remember to check if graph is normalized or not.
https://www.erinsaudiocorner.com/loudspeakers/https://www.audiosciencereview.com/forum/index.php?reviews/
I am illiterate in maths, but I like to look at pictures, like a child!
Check these measured results as spectrograms. Remember to check if graph is normalized or not.
https://www.erinsaudiocorner.com/loudspeakers/https://www.audiosciencereview.com/forum/index.php?reviews/
No. At some frequency several octaves below the baffle step frequency, the difference of SPL measured directly in front of the speaker and directly behind the speaker would equal zero, or nearly so. At some frequency several octaves about the baffle step frequency, the difference of SPL measured directly in front of the speaker and directly behind the speaker would be nearly be equal to the SPL reading taken in front of the speaker.
So the question is, assuming conditions that would exclude complicating factors, such as measurements taken far field in an anechoic chamber, what would be the difference of the two SPL readings (taken directly in front and behind the speaker) at the baffle step frequency? I'm looking for a specific number, such as 10 dB, 12 dB, 8 dB or whatever is correct. The ideal theoretical conditions might include Olson's spherical speaker box if that would make it easier to arrive at a solution.
Coming up with the answer I think would include an explanation of how the dB difference figure is arrived at, so to that extent I am asking what produces the baffle step.
Regards,
Pete
The way I visualise baffle step is that the speaker radiates sound as a sphere. The spheres size changes with frequency. If the sphere is smaller than the baffle, the rearward travelling portion of the sphere is bounced off the baffle, and adds to the output of the front travelling portion. (baffle reinforcement)
If the sphere is larger than the baffle, the sphere travels in all directions.
Depending on the shape of the baffle there will be some frequencies where parts of the sphere are larger than the baffle, and parts are smaller than the baffle. ie, there will be a transition area across a range of frequencies from full baffle reinforcement to no baffle reinforcement. The size and shape of baffle will affect this transition area.
For your question, maybe the best baffle shape to measure would be a circular flat baffle with the driver in the middle. This would reduce the step frequency to a single wavelength.
Rob.
If the sphere is larger than the baffle, the sphere travels in all directions.
Depending on the shape of the baffle there will be some frequencies where parts of the sphere are larger than the baffle, and parts are smaller than the baffle. ie, there will be a transition area across a range of frequencies from full baffle reinforcement to no baffle reinforcement. The size and shape of baffle will affect this transition area.
For your question, maybe the best baffle shape to measure would be a circular flat baffle with the driver in the middle. This would reduce the step frequency to a single wavelength.
Rob.
Pete,
This is all in the reference I linked in Post #2. Jason explains it very well.
You're asking the simple/classic 2pi/4pi radiation question......but in a very roundabout way. 🙂
The answer you're looking for is 3db.....if I'm understanding your question correctly.
Don't make it more complicated than it really is. 🙂
Dave.
This is all in the reference I linked in Post #2. Jason explains it very well.
You're asking the simple/classic 2pi/4pi radiation question......but in a very roundabout way. 🙂
The answer you're looking for is 3db.....if I'm understanding your question correctly.
Don't make it more complicated than it really is. 🙂
Dave.
https://sound-au.com/bafflestep.htm
6dB total difference from no baffle reinforcement to full baffle reinforcement, so I agree with Dave that we would have to assume 3dB right in the middle of the transition.
6dB total difference from no baffle reinforcement to full baffle reinforcement, so I agree with Dave that we would have to assume 3dB right in the middle of the transition.
This is not a quiz- I don't know the correct answer and explanation of how to arrive at it.
At a frequency several octaves above the baffle step frequency there is virtually 0 dB of sound to the rear.
Siegfried Linkwitz gave a presentation at Burning Amp (his last one before his death) that includes a plot of the phenomenon you are talking about. See slide 9 in the following pdf containing his presentation slides:
http://linkwitzlab.com/BA-2017/Radiation-BA2017.pdfYou can also listen to the presentation on YouTube:
The point that SL was making with these plots is that the baffle step of a boxed loudspeaker it is not happening the same, e.g. the baffle step curve is different, for various off axis angles around the loudspeaker. EQing the baffle step response to be flat is just making it worse (less flat) on some other axis. When the loudspeakers has a dipole response pattern the frequency response is the same shape, but different in level, as you move off axis. This is one reason why he was so interested in dipole loudspeakers. They have some major advantages over boxed loudspeakers (as well as generating some new problems, too!).
Yes, speakers start beaming once the wavelengths become smaller than the drive unit itself. A different phenomenon from baffle step.
Rob.
Maybe, instead of irritating everyone with statements like this, you could elaborate on your particular context/application??? Just a thought.
Dave.
Here is what is maybe the correct answer that I worked out. This is a very simple approach. Acoustics is something that I have been interested in for some time, but what i know about it I have only learned about on my own. So take this with a grain of salt. 😳
At some frequency well below (several octaves) the baffle step frequency sound pressure behind and in front of the speaker system is the same. That same sound pressure equals 1.
At the baffle step frequency sound pressure of the front wave has increased to 1.414 as 20*log1.414 = 3 dB.
Any sound pressure added to the front wave must be pressure taken away from the rear wave. Thus SPL of the rear wave becomes,
1- 0.414 = 0.59
Solving for the change of SPL of the rear wave at the baffle step frequency,
20*log0.59 = -4.58 dB
At the baffle step frequency,
dB difference = 3 dB -(-4.58 dB) = 7.58 dB
At some frequency well below (several octaves) the baffle step frequency sound pressure behind and in front of the speaker system is the same. That same sound pressure equals 1.
At the baffle step frequency sound pressure of the front wave has increased to 1.414 as 20*log1.414 = 3 dB.
Any sound pressure added to the front wave must be pressure taken away from the rear wave. Thus SPL of the rear wave becomes,
1- 0.414 = 0.59
Solving for the change of SPL of the rear wave at the baffle step frequency,
20*log0.59 = -4.58 dB
At the baffle step frequency,
dB difference = 3 dB -(-4.58 dB) = 7.58 dB
The pressure all starts in one place. With frequencies above baffle step the sound waves or whatever do not travel round the back of the speaker, get subtracted and then get placed back at the front to add to the front wave. They never get round the back of the speaker in the first place.
IOW, it's all one pressure, just being distributed differently according to baffle size / shape, and wavelength.
This at first seems like a "smart" approach using logic, math, etc. Unfortunately the answer is completely wrong.
Like I posted above, see Linkwitz's pdf to get the value you are looking for. It's the upper plot on slide #9. Just read the SPL value right off of the plot at the halfway point of the baffle step response curve for any of the angles he has plotted.
Is slide 9 on page 9 of the pdf? If so, and I'm looking at the top graph on p.9, is the X axis .01, .1. and 1 times the baffle step frequency? I suppose I could find out by watching the video which maybe i will do tomorrow.
Thanks,
Pete
These simulation results should help to answer the question. There is a 300mm wide cabinet that is 250mm deep with a simulation of a Satori WO24 woofer.
This is the 180 degree response and normalized polar, the area of greatest null is around 160 degrees off axis.
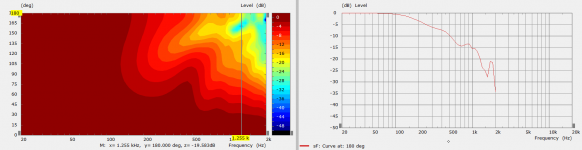
This is the normalized plot at 160 degrees.
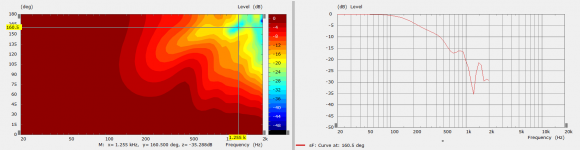
This is the plot without normalization at 160 degrees.
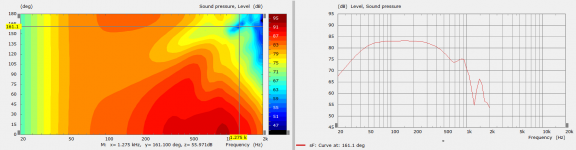
The greatest rejection is close to the wavelength of the baffle width which is 1146 Hz.
There are two steps in the directivity related to baffle size and box size. The first step is when the baffle is no longer constraining radiation and the second related to the width and depth of the cabinet combined. This image shows it clearly.
How much of an effect the shape and depth has varies quite a lot.