Question for Geddes and John K

[Borat]

Did you know that Porsche designed a hybrid electric vehicle in 1941? It was called the Elephant. A diesal engine driving a generator and electric motors on each track. The first "production" use of such a system to my knowledge.

Yes. Germany FTW !

http://www.box.net/shared/static/96q3fvikdu.mp3

if i was a brainwashed lemming i should be outraged that all these German companies have a past in building weapons for Hitler. i should also be outraged at the CO2 that some of the high performance cars produce.

unfortunately i know that politicians are the same everywhere. Bush's grandfather was financing Hiter for example. And global warming is a lie.

Therefore long live Porsche, BMW, Audi and Mercedes.

 

[thadman]

Yes. Germany FTW !

http://www.box.net/shared/static/96q3fvikdu.mp3

if i was a brainwashed lemming i should be outraged that all these German companies have a past in building weapons for Hitler. i should also be outraged at the CO2 that some of the high performance cars produce.

unfortunately i know that politicians are the same everywhere. Bush's grandfather was financing Hiter for example. And global warming is a lie.

Therefore long live Porsche, BMW, Audi and Mercedes.

It should be no surprise that those companies produced weapons for Hitler.

I'm sure Hitler acquired the best minds that were available within the state for research and development. The U.S. acted along similar lines with the Manhattan project.

I'm sure many engineers would consider working on advanced projects with significant funding, even if the pay wasn't the best.

Example: NASA

I'm sure many of the engineers/scientists at NASA could operate their own businesses and probably make more money doing it. However, they will never have the checkbook that the government possesses.

Following defeat, there was no longer a source of funding for the engineers. What were they supposed to do, start gardening? The auto industry was a natural segway for these engineers as there was significant funding in place.

Point is: R&D follows funding. Politicians control funding (ahem, global warming). It is not necessarily a direct reflection of the engineers.

 

[john k...]

It didn't read like that.



"a succession of pulse may result in greater heating" - no John, it WILL result in greater heating - two pulses, twice the heat, three, three times, etc. It doesn't take many pulses until you have a lot of heating. Your own data showed that a tweeter has time constants on the order of ms - thats what "over time" means here. Its not the effect on a single impulse that I am concerned with but the effect on a string of them, ala noise or music. I think you are looking at it the wrong way.

I looked at your results and see support that it is a possibility and you see it otherwise - what can I say.

Earl,

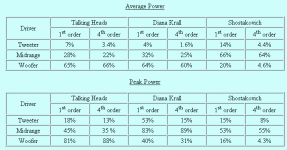
You completely miss what these figures are saying. Remember, cooling has been ignored. Thus looking at this figure which is for 28.3 V and goes out to 1 sec. it tells me the following. If the temperature at the application of the pulse is T*, then I can compute (T*-To)/To and go to the time, t*, location on the red curve where (T-To)/To is equal to that value. That is the t=0 for the pulse. Then if the pulse I am considering has a duration of td, the pulse ends at t= t*+ td on the plot. I can read the value of (T-To)/To at that time call it (T**-To)/To. Then, backing out T**, (T**-T*) is the rise in VC temp dues to the pulse. But the rise will always be greatest between t = 0 and t = td. That is the rise will always be greastest when starting at room temperature.

An externally hosted image should be here but it was not working when we last tested it.

Now, since cooling is not yet considered, it makes no difference is I have 1 pulse of 100 msec duration or 100 pulses of 1 msec duration. The maximum change in VC temperature due to either (regardless of spacing between pulses) is given for any starting temperature by locating the time where (T-To)/To is equal to the value for the starting temperature and then going out 100 msec. to find the rise. For example, 1 pulse of 1 sec duration starting from T= To, or 1000, 1 msec pulses in succession will yield a rise in (T-To)/To to 2.0, or the VC temp will be 3 To at the end of 1 sec. This is the maximum rise in temperature that could occur. If there were cooling involved, and each of the 1000 pulses were separated by some finite time, then the rise would be less dues to the relaxation between pulses. Like wise, if it was a single 1 sec pulse, the rise would be less because the rate of increase would decrease as time went by because of cooling.

I don't disagree that the multiple pulses results in heating of the VC over time. And while the first pule in the 1000 pulse chain would be reproduced at the 110.5dB level, the 1000th pulse would be at 108.74dB. So, yes, there may be compression due to thermal effects (I say may because with cooling it is possible the temperature relaxes back to the value at the start of the pulse, depending on the interval between pulses). That is not in dispute. But, and I guess there is were Internet terminology gets in the way, I would not refer to that as dynamic compression. To me that is just compression due to longer term operation at high power. When I think "dynamic compression" I am thinking of a case where the temperature rise actually alters the amplitude over the duration of a short term (like 1 msec) pulse. That is a short term, high amplitude dynamic event, like a rim shot, actually suffers "self compression. So, yes, the 1000th pulse is reproduced at a level 1.76dB lower than the 1st, but the difference between the 999th and 1000th is negligible. Self compression is negotiable if the duration of the event is short, short be defined arbitrarily as, for example, not more that 1/2 dB or what ever you like. 1/2dB would translate to no more that a 12% increase in Re over the transient or a 30 degree C temperature rise. If you like 0.1 dB then a 2.3% increase in Re or a 6 degree C rise.

As I said, I performed the analysis w/o bias. How the web page reads reflects my interpretation of the results.

Furthermore, looking at the last plot which probably should be first (but I didn't think about that until I saw the results of the analysis) if the operating temperature of the VC stays below 400 C (which I suspect is extreme considering the comments about ferrofluid from the manufacture), then the entire thermal compressing thing is limited to about 2 dB, significant, but not dramatic.

An externally hosted image should be here but it was not working when we last tested it.

We can argue about the interpretation but not the results. The analysis is simple and straight forward: Heat in goes to increase in T.

 

[gedlee]

So, yes, there may be compression due to thermal effects (I say may because with cooling it is possible the temperature relaxes back to the value at the start of the pulse, depending on the interval between pulses). That is not in dispute. But, and I guess there is were Internet terminology gets in the way, I would not refer to that as dynamic compression. To me that is just compression due to longer term operation at high power. When I think "dynamic compression" I am thinking of a case where the temperature rise actually alters the amplitude over the duration of a short term (like 1 msec) pulse.

We can argue about the interpretation but not the results. The analysis is simple and straight forward: Heat in goes to increase in T.

John, goods points, several counter points.

1) as to "dynamic" it all depends on the time constants involved, just as I have said from the begining. It is not a steady state analysis and so it is "dynamic", but its not on the order of a single pulse we agree on that, but music is not a single pulse.

Here is a point that I thought of last night: Consider a noise signal from 0 Hz to 10 kHz (convenient numbers). Now, as I am sure that you know, the Power Spectral Density (PSD) is in V^2 / Hz - thats linear Hz not log Hz. That means that the power disipate in a tweeter crossed over at 1 kHz is 9 time the power disipated in the woofer (0-1 kHz versus 1-10 kHz). As your analysis shows the tweeter is the most sensitive and yet it is getting 90% of the power. Now if that not a cause for concern I don't know what is. Your analysis assumed the tweeter gets a small amount of the thermal power when in fact it gets the vast majority of it.

Music is not distributed uniformly in frequency and thats a factor, but not enough to change the conlusions.

And if you did your analysis in % change, as we do for nonlinear distortion, then the numbers would be very large. Thats why I dispute the use of dB. Many think that nonlinear distortion is audible, but on a dB scale it is much less that the thermal modulation that we are talking about here. THD does change the amplitude of the waveform by even .5 dB, but people claim thats audible (I don't of course, but thats not the point). The thermal changes are at least an order of magnitude greater than the changes due to nonlinearity.

They are entirely different things, granted, but we just cannot go about saying that one is audible and the other not when the one being claimed as inaudible is much the much greater effect than the one claimed is audible. It just doesn't make sense. Maybe they are both inaudible, thats possible, and it's something else entirely. But what it cannot be is nonlinearity is audible and thermal is not. There is far too much data to say that is not the case.

The results depend on the analysis and I didn't check that so I can't say either way. But as I said, I saw the results as confirmation of my points so I didn't see any reason to question them - just your conclusions.

 

[Robh3606]

Your analysis assumed the tweeter gets a small amount of the thermal power when in fact it gets the vast majority of it.

Wow I am confused. This can't be the same as PSD in music content. I always thought it was the opposite where all the power is in the low end. We talking apples and oranges or do I have it wrong?? Does it make sense to consider the PSD in program content to simulate a real world application??

Rob🙂

 

[gedlee]

Wow I am confused. This can't be the same as PSD in music content. I always thought it was the opposite where all the power is in the low end. We talking apples and oranges or do I have it wrong?? Does it make sense to consider the PSD in program content to simulate a real world application??

Rob🙂

It makes sense to consider the actual power delivered to the driver and a single impulse is hardly sufficient.

A lot of poeple don;t realize how much electrical power gets put into the high frequencies because they are always looking at log frequency scales. But power is not logarithmic. This is why white noise sounds so bright and pink noise nuetral. Pink noise might be a better example for this situation in which case the power below 1 kHz is about three times that above. More reasonable, but still, a tweeter, which is at least ten times more sensitive than a woofer will still receive 1/3 the power of the woofer making it still a concern. My only point here is that a single impulse IS NOT the issue. It is power we are talking about here and you have to use power numbers that are relavent.

 

[markus76]

This discussion leads us nowhere. It just serves defining a new "belief system". We already have too much of them in audio.

All we need to do is measure. Real loudspeakers with real music at calibrated levels. Someone smarter than me would need to define a way to derive the amount of dynamic compression from that data.

 

[gedlee]

This discussion leads us nowhere. It just serves defining a new "belief system". We already have too much of them in audio.

All we need to do is measure. Real loudspeakers with real music at calibrated levels. Someone smarter than me would need to define a way to derive the amount of dynamic compression from that data.

Not true Markus. All understanding comes from a hypothesis, you need that first. The more concrete and based in scientific fact this hypothesis is the better quantified the proposed tests will be. Then testing is necesary as you suggest, but not with music since that is too hard to quantify and there is no "standard". Noise is a better source since it can be defined very precisely in mathematical terms to have "comparable" statistics to music. I have done the music statistics and they are all over the map - no consistancy whatever. So noise targeted at the "mean" values of music is the best source.

I have already done a lot of that. I have a hypothesis, as stated, even though some discount it - thats fine as long as its based on facts. I have tested this hypothesis and found that there is significant thermal modulation of a loudspeaker system with signal. What the issue is now, in my mind, is precisely what John points out - what are the time constants involved. I do not know the time constants involved enough to know if this is truely "dynamic" or simply another approach to what is basically hust the steady state thermal compression. I have a test that I believe will tell me that and I have taken data. I have not had the chance to analyze that data.

Now, if there are time constants short enough to be significant, say < 10 ms and there temperature changes are sufficient to cause say 10-20% change in the levels of any parts of the waveform, then a subjective test would then be required to determine the metric for audibility.

So this is not just an achademic exercize as you suggest. It's a scientific study and to do it right requires patience and diligence to get to the real facts. You just cannot "jump to the answer" as you imply. Thats what audiophools usually do and they usually get it wrong because not enough controls are in place to get at the facts.

 

[catapult]

It makes sense to consider the actual power delivered to the driver

Art Ludwig analyzed 3 music clips in Matlab and simulated crossovers at 300 and 3K, either 1st order or 4th order. There was little peak power going to the tweeter with either Shostakovich or Talking Heads. Diana Krall had a higher percentage but that's not the kind of music you listen to really loud. The numbers assume equal-efficiency drivers and he explains why they don't all add up to 100%.

Music and the Human Ear

 

[Robh3606]

Someone smarter than me would need to define a way to derive the amount of dynamic compression from that data.

I think someone already has. It's available on some of the JBL system spec sheets we have over at Lansing Hertage. On some of the newer systems they have a less than .5db power compression spec. @ 100dB. I am assuming that's at 1 meter. It's the only place I have ever seen a power compression limit even mentioned on commercial speakers. I have seen it published on the Pro stuff and the non powered monitors.

Rob🙂

 

[gedlee]

Art Ludwig analyzed 3 music clips in Matlab and simulated crossovers at 300 and 3K, either 1st order or 4th order. There was little peak power going to the tweeter with either Shostakovich or Talking Heads. Diana Krall had a higher percentage but that's not the kind of music you listen to really loud. The numbers assume equal-efficiency drivers and he explains why they don't all add up to 100%.

Music and the Human Ear

Dennis

Thanks. Given the high crossover point of 3 kHz as opposed to 1 kHz, those number all look reasonable. And by no means is the tweeter sheltered from the power input given the fact that it is far more sensitive than the other two drivers. Its going to be the tweeter that has problems and this is waht all my measurements said. For two-way with a typical 1" tweeter the modulation at 10 kHz was almost 10 dB, but this was far more steady state stuff so that number is high for the more dynamic short term situation.

 

[john k...]

John, goods points, several counter points.

1) as to "dynamic" it all depends on the time constants involved, just as I have said from the begining. It is not a steady state analysis and so it is "dynamic", but its not on the order of a single pulse we agree on that, but music is not a single pulse.

Here is a point that I thought of last night: Consider a noise signal from 0 Hz to 10 kHz (convenient numbers). Now, as I am sure that you know, the Power Spectral Density (PSD) is in V^2 / Hz - thats linear Hz not log Hz. That means that the power disipate in a tweeter crossed over at 1 kHz is 9 time the power disipated in the woofer (0-1 kHz versus 1-10 kHz). As your analysis shows the tweeter is the most sensitive and yet it is getting 90% of the power. Now if that not a cause for concern I don't know what is. Your analysis assumed the tweeter gets a small amount of the thermal power when in fact it gets the vast majority of it.

Music is not distributed uniformly in frequency and thats a factor, but not enough to change the conlusions.

And if you did your analysis in % change, as we do for nonlinear distortion, then the numbers would be very large. Thats why I dispute the use of dB. Many think that nonlinear distortion is audible, but on a dB scale it is much less that the thermal modulation that we are talking about here. THD does change the amplitude of the waveform by even .5 dB, but people claim thats audible (I don't of course, but thats not the point). The thermal changes are at least an order of magnitude greater than the changes due to nonlinearity.

They are entirely different things, granted, but we just cannot go about saying that one is audible and the other not when the one being claimed as inaudible is much the much greater effect than the one claimed is audible. It just doesn't make sense. Maybe they are both inaudible, thats possible, and it's something else entirely. But what it cannot be is nonlinearity is audible and thermal is not. There is far too much data to say that is not the case.

The results depend on the analysis and I didn't check that so I can't say either way. But as I said, I saw the results as confirmation of my points so I didn't see any reason to question them - just your conclusions.

No argument with what you are saying but you are misinterpreting the tweeter results. The power delivered to the tweeter is E^/Re in the analysis. E could represent the magnitude of a flat top pulse or a step. That power is dissipated constantly over time in the analysis. The filtered impulse I showed is just to indicate that if, for example, a speaker with a 1 KHz LR2 high pass tweeter filter was subjected to a step change in input from 0 V to E, then what the tweeter would see is the a sharp rise in level , followed by a decay to zero in less then 1.25 msec. Therefore, in the analysis I argued that a flat top pulse of 1.25 msec would represent much more power than would be actually dissipated int he tweeter as a result of that application of a step change in input voltage to the speaker. On the other hand, if the speaker were subject to a steady sine wave at 5 Kz with RMS amplitude = E, then the analysis would represent the growth of the temperature, on average to, that signal. The actually increase in T would be a stair case affair, but the trend would be the same (same average rate of increase). In such a case,the analysis would show the temperature rising until the VC melted since no cooling is in the analysis.

One other thing I have to correct. I stated that the calculations were for room temperature and wrote 63 C. That is in error, as room temp = 20 C. The calculations are correct, but to calculate the temperature the from the curves use T = 20 + (T-To) x 63. That is, the temperature rise is correct, but normalized by the wrong reference temperature. I may replace the figures with corrected ones later today so there is no confusion.

Regarding the compression in percent, -1dB is roughly a 10% reduction in amplitude. What I might suggest is to take a waveform with a sharp peak and compress the peak nonlinearly as an exercise and compare harmonic content. I.e, A(t) = A(input) x C(A) where C(A) would be 1 and maybe exponentially approach 0.9 as A(input) approaches 1.0 so there would be no compression at low amplitude.


P S: I will probably have something with cooling in ti tomorrow. I have some ideal on how to get a reasonable estimation of the cooling rate.

 

[gedlee]

No argument with what you are saying but you are misinterpreting the tweeter results. The power delivered to the tweeter is E^/Re in the analysis. E could represent the magnitude of a flat top pulse or a step. That power is dissipated constantly over time in the analysis.

Then I don't agree with what you are doing since this is not really a spectral power approach at all and basically can't get there from here. To do this problem correctly you must look at the spectrum or PSD of the signal from which you can get the power disipated for an arbitrary signal, use that to calculate the temp and hence the Re. From this you can track how the power will affect the actual signal "dynamicly". This is why I refered to your analysis as "quasi-steady state" and why I think the results were misleading.

 

[Key]

Would correlation with real music examples show anything meaningful? I don't think the feature is working 100% accurately in Holm but it's an idea of how to measure with real music signals.

 

[gedlee]

Would correlation with real music examples show anything meaningful? I don't think the feature is working 100% accurately in Holm but it's an idea of how to measure with real music signals.

That is what I do, but corelation takes many forms. Autocorrelation is a statistical process that gives you frequency domain statistics and the PSD. I use histograms to give me amplitude domain statistics, basically sets the PDF of the amplitudes - noise is always Gaussian, unless you do something with it - but it can simulate the types of PDF and PSDs seen in music. If you have comparable PDFs for the amplitides and PSD for the frequencies then for all practical purposes the signals are the same - except for the envelope. But this can be modulated to simulate music. Of course one is highly coherent and the other random and so they will sound different, but from a thermal aspect - most engineering aspects in fact - they are the same.

 

[Key]

Are they the same though? It just seems to me there are a lot of wiggles and bumps in real music and I just don't know if correlation testing with real music would uh... correlate with correlation testing with noise and tones. I could see them being pretty much the same though. But when it comes down to it I haven't done enough of it or seen enough of it done to have an opinion.

And I guess I was thinking it would be less theory and easier to pin down. For instance all you need to do is for a given set of speakers that display compression characteristics play a bunch of music until you find a portion of music which you think induces dynamic compression. You then use that music passage as the test tone and do a correlation with it. It wont show you THD but you said you aren't looking for that - so I would expect amplitude distortions right?

 

[gedlee]

find a portion of music which you think induces dynamic compression.

Not very scientific.

 

[john k...]

Then I don't agree with what you are doing since this is not really a spectral power approach at all and basically can't get there from here. To do this problem correctly you must look at the spectrum or PSD of the signal from which you can get the power disipated for an arbitrary signal, use that to calculate the temp and hence the Re. From this you can track how the power will affect the actual signal "dynamicly". This is why I refered to your analysis as "quasi-steady state" and why I think the results were misleading.

Let's put if this way. In either case we need to know s(t), the input signal. My next step with cooling is a transient approach. Thus, I will integrate

dT/dt = Q' -L'

where Q' is the generation (s(t)^2/Re) and L' represents the losses. Thus I will compute T(t) directly. PSD will tell you how much power is dissipated at what frequencies but I don't think it will tell you when. And besides, AFAIK, the PSD requires that the signal be stationary. Random noise is stationary, a musical signal is not.

 

[Key]

lol you always forget who you're talking to 🙂 I wouldn't just use one. But average over many examples to see the behavior of the VC under dynamic compression. And it's just a weird way to correlate what the actual problem is - subjective perception of dynamic compression artifacts.

 

[thadman]

With regards to a transient,

Is anyone aware of any psychoacoustics tests which attempted to quantify the audible threshold for a thermally compressed pulse? 10% 1% .1%?