So the initial tone at 1Khz works well, it looks like it's 1KHz, centre 10KHz and 2KHz/division:
I have noise - this is mostly from the open tube chassis I have connected the probes inside.
10KHz:
20KHz moved across a little
I have noise - this is mostly from the open tube chassis I have connected the probes inside.
10KHz:
20KHz moved across a little
Last edited:
So two main improvements can be made:
First - zero crossover detection
When the data buffer is created, a zero crossover can be used - this detects the last crossover sign change and allows the data to be adjusted so that there's a seamless crossover.
Now I have the code for zero crossover in the next version, however it's not fully working because of point 2 (it assumes a start at zero).
Second - reduce change latency
When the 1104 does it's bode plot to sweeps slowly and gets faster as it gives up the logarithmic scale. The current code has a limitation in that frames per buffer is set to 44100 - ie a full second of audio per buffer fill. This means that the minimum time between the pitch changes is 1 second. Not fast enough for the 1104. So I'm trying the reduction of the buffer fill to 1/10th the size or 0.1 second. This means more python callbacks and higher CPU but less problems with the 1104.
The initial results seem promising.
The complication is attempting to keep as much out of python as possible - using only the numpy and pre-compiled code/libraries as possible. Also pre-calculating the output required for each buffer fill (as much as you can) - this has to be done dynamically at callback to fill the next set of data.
The C version of a callback has the luxury of being fast enough to conditionally fill a buffer. The python less so.
It's close but not there just yet.
Normally python is easily fast enough to generate samples on the fly for reasonable samplerates and channel counts. In your case of virtualbox running on small mac ntb your mileage may vary but I would be surprised if it were too slow to generate a single stream at 48kHz.
Typically the blocks generated between callbacks are not so long, just tens of ms. That gives you a reasonable latency and reaction time to commands. The buffers generated do not have to contain whole periods (which conflicts with the fixed buffer size for various frequencies), just make them continue from the phase where the previous buffer ended.
If I were to code the thing, I would make a generator which takes number of samples, final phase of the previous buffer, current required frequency, sample period time. Using this info I would the generate number of samples, at the required frequency, starting at the last phase + phase shift of sample period time for the current required frequency (sample n+1). All this can easily be generated with numpy. The generator would return the generated array and phase of the last sample, to be remembered for the next cycle. This can be generated in the callback.
This would allow keeping the phase continuous, even if the required frequency changes to a new value. If needed, a linear sweep from f_prev to f_new can be easily implemented e.g. within one buffer callback to allow even smoother transition, again efficiently with numpy (precalculate vector with sine phases for each sample, each phase corresponding to linearly interpolated frequency for the given sample, and pass that to sine calculation, instead of time vector * 2 * pi * frequency). To simplify, this method could be used for generating the fixed frequency too (with f_prev = f_new). That would automatically sweep from f_prev to f_new within one callback and than stay at f_new.
Many ways possible.
Typically the blocks generated between callbacks are not so long, just tens of ms. That gives you a reasonable latency and reaction time to commands. The buffers generated do not have to contain whole periods (which conflicts with the fixed buffer size for various frequencies), just make them continue from the phase where the previous buffer ended.
If I were to code the thing, I would make a generator which takes number of samples, final phase of the previous buffer, current required frequency, sample period time. Using this info I would the generate number of samples, at the required frequency, starting at the last phase + phase shift of sample period time for the current required frequency (sample n+1). All this can easily be generated with numpy. The generator would return the generated array and phase of the last sample, to be remembered for the next cycle. This can be generated in the callback.
This would allow keeping the phase continuous, even if the required frequency changes to a new value. If needed, a linear sweep from f_prev to f_new can be easily implemented e.g. within one buffer callback to allow even smoother transition, again efficiently with numpy (precalculate vector with sine phases for each sample, each phase corresponding to linearly interpolated frequency for the given sample, and pass that to sine calculation, instead of time vector * 2 * pi * frequency). To simplify, this method could be used for generating the fixed frequency too (with f_prev = f_new). That would automatically sweep from f_prev to f_new within one callback and than stay at f_new.
Many ways possible.
Last edited:
That is pretty much what it does and the redesign of the internals.
Python my have some speed but as this is my first python programming it’s a painful experience. Doubly so due to focusing on numpy todo the CPU intensive work.
Python my have some speed but as this is my first python programming it’s a painful experience. Doubly so due to focusing on numpy todo the CPU intensive work.
It seems happy making the tone you want although I detected something and managed to catch this on the scope
The issue is when it switches tone.
The issue is when it switches tone.
Done - it works 😀
1. I've switched from 44.1K to 192K - this solved the issues further up the frequency range.
2. Did sums on paper then moved them across - I'd got confused and so this solved it all.
3. Cleaned up and added a mute although I disable it.
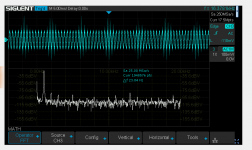
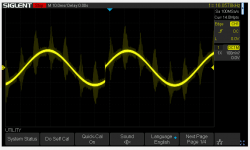
Just testing a 16KHz sine wave and this looks reasonably tidy:
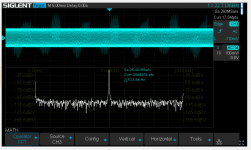
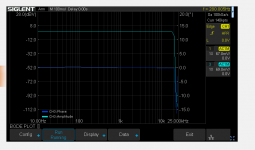
Proof of the pudding, a bode plot Vin dbV which shows the Mac mini headphone filter rolloff:
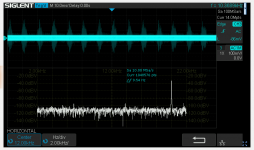
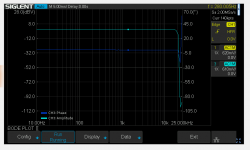
Several cycles later - it still shows the same profile:
Code for your pleasure:
1. I've switched from 44.1K to 192K - this solved the issues further up the frequency range.
2. Did sums on paper then moved them across - I'd got confused and so this solved it all.
3. Cleaned up and added a mute although I disable it.
Just testing a 16KHz sine wave and this looks reasonably tidy:
Proof of the pudding, a bode plot Vin dbV which shows the Mac mini headphone filter rolloff:
Several cycles later - it still shows the same profile:
Code for your pleasure:
Last edited: