Phono preamp: RIAA EQ using IIR digital filters

[jiiteepee]

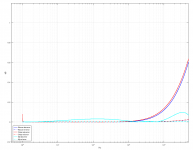
If you need better overall response for 96kHz filter, I suggest using my 3rd order coefficients instead of Orban's/Wurcer's 4th order (2x biquad) coefficients (error plot attached). My 3rd order MZT/MIM based coefficients are:

b = [0.112505293158829  -0.033756941867625  -0.066435946167708  -0.006063956599930];
a = [1.000000000000000  -1.378665728551891  -0.044341939523520   0.423638954754309];

Coefficients based on Orban's poles/zeros:

z = [-0.4510059, -0.1619979, -0.2531282E-01, 0.9678047];
p = [-0.3815793, -0.8907574E-01, 0.8703285, 0.9967329];

are:

1.000000000000000e+00   6.130038000000005e-01   7.306200868761005e-02   1.000000000000000e+00   4.706550399999999e-01 3.398945851618199e-02
1.000000000000000e+00  -9.424918799999991e-01  -2.449786616625399e-02   1.000000000000000e+00  -1.867061400000001e+00 8.674850497576508e-01

Wurcer's 4th order (2 x biquad) implementation can be found from his article.

 

[ariendj]

If you need better overall response for 96kHz filter, I suggest using my 3rd order coefficients instead of Orban's/Wurcer's 4th order (2x biquad) coefficients (error plot attached). My 3rd order MZT/MIM based coefficients are:

b = [0.112505293158829  -0.033756941867625  -0.066435946167708  -0.006063956599930];
a = [1.000000000000000  -1.378665728551891  -0.044341939523520   0.423638954754309];

Coefficients based on Orban's poles/zeros:

z = [-0.4510059, -0.1619979, -0.2531282E-01, 0.9678047];
p = [-0.3815793, -0.8907574E-01, 0.8703285, 0.9967329];

are:

1.000000000000000e+00   6.130038000000005e-01   7.306200868761005e-02   1.000000000000000e+00   4.706550399999999e-01 3.398945851618199e-02
1.000000000000000e+00  -9.424918799999991e-01  -2.449786616625399e-02   1.000000000000000e+00  -1.867061400000001e+00 8.674850497576508e-01

Wurcer's 4th order (2 x biquad) implementation can be found from his article.

Wow that's neat, thanks for sharing this! Will definately give these coefficients a try. It'll take some time until I get my setup back together though. But it's something to look forward to 🙂

 

[jiiteepee]

If you need better overall response for 96kHz filter, I suggest using my 3rd order coefficients instead of Orban's/Wurcer's 4th order (2x biquad) coefficients (error plot attached). My 3rd order MZT/MIM based coefficients are:

b = [0.112505293158829  -0.033756941867625  -0.066435946167708  -0.006063956599930];
a = [1.000000000000000  -1.378665728551891  -0.044341939523520   0.423638954754309];

Coefficients based on Orban's poles/zeros:

z = [-0.4510059, -0.1619979, -0.2531282E-01, 0.9678047];
p = [-0.3815793, -0.8907574E-01, 0.8703285, 0.9967329];

are:

1.000000000000000e+00   6.130038000000005e-01   7.306200868761005e-02   1.000000000000000e+00   4.706550399999999e-01 3.398945851618199e-02
1.000000000000000e+00  -9.424918799999991e-01  -2.449786616625399e-02   1.000000000000000e+00  -1.867061400000001e+00 8.674850497576508e-01

Wurcer's 4th order (2 x biquad) implementation can be found from his article.

I used old (from ~2005) zero-pole data for Orban's 4th order filter coefficients. Here are newer (from 2007) but 3rd order data taken from his comp.dsp post back in 2007:

poles and zeros

z = [-0.3096394, -0.4513594e-01, 0.9677730];
p = [-0.1992839, 0.8703280, 0.9967002];

which results to a 3rd order filter coefficients:

b = 1.141249286497031e-01 -6.995831420993498e-02 -3.758888605595347e-02 -1.543592747073277e-03
a = 1.000000000000000 -1.667744300000000 0.495387430559620 0.172870033025878

Second order sections are then:

1.000000000000000   0.354775340000000   0.013975865380036   1.000000000000000  -0.671044099999998  -0.173442358119200
1.000000000000000  -0.967773000000000                   0   1.000000000000000  -0.996700200000003                   0

Attached error plot shows similarity between Orban's and Wurcer's calculation methods.