Note:This is split from this thread:
What do you think makes NOS sound different?
As you know, our test files are produced via the PGGB upsampling software. This is because it’s the highest performing audio resampling filter of which I’m aware. My only reservations regarding the PGGB have been it’s cost, which reflects it’s performance. (A quick aside, if you recall, our thread members are generously offered a 50% discount by ZB, author of the PGGB). Plus, the fact that it’s extreme performance necessitated it work offline. In other words, it doesn’t support real-time streaming content, such as from disc or the internet.
First, a disclaimer. I believe the below information to be correct, however, the responsibility is on you to verify all details. That said, ZB has just released an essentially real-time version of the PGGB, and which functions as a Foobar2000 plug-in. Even better, this Foobar version is free for download and use! So, you now may upsample, downsample, dither and experiment to your heart’s content, and at no cost.
As I understand it, the main performance limitation here is the maximum number of filter taps. Which is ONLY 2-million, in the free version. If you desire, a license may be optionally purchased which expands the maximum filter taps to 1-billion. For reference, the offline version PGGB supports a maximum of 8-billion taps. Ridiculously large figures for an interpolation-filter in either case. It’s an effective business strategy when a company manifestly believes in the benefits of it’s product. No risk for potential users to find out what PGGB technology may do for their listening enjoyment. Enough talking by me. Below is a link to the ‘remastero’ website with the intriguing details.
foo-RT - ZB's Guide
What do you think makes NOS sound different?
As you know, our test files are produced via the PGGB upsampling software. This is because it’s the highest performing audio resampling filter of which I’m aware. My only reservations regarding the PGGB have been it’s cost, which reflects it’s performance. (A quick aside, if you recall, our thread members are generously offered a 50% discount by ZB, author of the PGGB). Plus, the fact that it’s extreme performance necessitated it work offline. In other words, it doesn’t support real-time streaming content, such as from disc or the internet.
First, a disclaimer. I believe the below information to be correct, however, the responsibility is on you to verify all details. That said, ZB has just released an essentially real-time version of the PGGB, and which functions as a Foobar2000 plug-in. Even better, this Foobar version is free for download and use! So, you now may upsample, downsample, dither and experiment to your heart’s content, and at no cost.
As I understand it, the main performance limitation here is the maximum number of filter taps. Which is ONLY 2-million, in the free version. If you desire, a license may be optionally purchased which expands the maximum filter taps to 1-billion. For reference, the offline version PGGB supports a maximum of 8-billion taps. Ridiculously large figures for an interpolation-filter in either case. It’s an effective business strategy when a company manifestly believes in the benefits of it’s product. No risk for potential users to find out what PGGB technology may do for their listening enjoyment. Enough talking by me. Below is a link to the ‘remastero’ website with the intriguing details.
foo-RT - ZB's Guide
Last edited:
A linear phase filter with 2 million taps has 11.3379 seconds of group delay at 88.2 kHz, 2.6042 seconds at 384 kHz. With 1 000 000 000 taps, that would be 1 hour, 34 minutes and 28.93 seconds at 88.2 kHz and 21 minutes and 42.08 seconds at 384 kHz.
So for the maximum number of taps, when you interpolate CD audio by a factor of two, you start hearing the first track long after the CD has finished.
This gets a bit inconvenient for real time use. Are there any tricks used like skipping some taps after initialization or filling the filter at an increased speed?
So for the maximum number of taps, when you interpolate CD audio by a factor of two, you start hearing the first track long after the CD has finished.
This gets a bit inconvenient for real time use. Are there any tricks used like skipping some taps after initialization or filling the filter at an increased speed?
Last edited:
ZB hasn't discussed the details with me, Marcel, so I can only point to the below sentences from his linked website:
"...We say 'near real-time' because remastering using insanely long filters require a finite time. Depending on the length of your track and the filter length (in millions of taps) you choose, the very first track will take anywhere from a few seconds to a few ten seconds to start. The subsequent tracks would play in a gap-less fashion."
I presume that is only true for tracks stored on disc, or in other local mass storage, but not true for non-local streaming files, such as from an Internet based music service. However, I don't know. I feel rather sure that ZB would clarify if asked.
Last edited:
You're filling chains of flip-flops for hardware (or, basically the same for software) digital FIR filters. You can't fill them faster than your clockrate without a degradation in quality. You could feed-forward copies of the sample at 8x 16x, etc. the rate as direct copies, but this might lead to audible artifacts. There's no crystal ball for causality in an LTI system.
The obvious way to do this is to oversample by an insane amount, reducing the bitrate as necessary because you don't have enough data to resolve accurately (converting amplitude accuracy to time accuracy), then use a feedback mechanism to force the generated noise to an inaudible frequency, and finally filter the output to remove the high-frequency noise. (See sigma-delta modulators and DSD audio)
You can apply your filters after the oversampling since you have the clockrate to do so already.
Last edited:
If you can somehow read the input data at a higher than normal rate, you can first fill almost half the filter at an increased rate, then go back to the normal sample rate and turn on the output. That would not work for streaming or any other application where the data only become available at the normal sample rate.
Hi Marcel,
When I’m right it takes even twice the time before the filter starts producing output.
To fill 2M taps at 88.2 for the first time takes 22.67 sec. The GD after being filled is then indeed 11.34 sec but it is the 22.67 sec delay you have to wait before the music starts playing.
Hans
I think the music starts playing immediately but at such a low level that you probably won't notice it, until the first samples reach the taps with large weights near the centre of the filter.
Exactly. If you would mute the output until the filter is completely filled, you would miss the first 11 seconds.
If you can just buffer the whole file and keep the buffer filled, this becomes a non-issue, of course. I was thinking in regards to limited input bandwidth. Even with streaming (modern, not CD transport), there's buffering happening.
Yes, true as always. Think of it as if the file was preceded by 11seconds undithered silence.
Hans
ZB's speaks about PGGB-RT latency
I received the below email from ZB this morning. It regards our thread discussion on the PGGB-RT playback latency.
================================================
I saw some questions raised regarding tap length and delays and feasibility of doing the upsampling (or downsampling) in real-time.
The tap lengths are the maximum PGGB will use but they are not used all the time if the length of the track is not long enough. The taps are for the output rate. So choosing 2M and setting an output rate of 88.2kHz implies a maximum of 2M taps would be used at 88.2kHz and the track length has to be longer than or equal to 2M at the output rate, else the number of taps used will be reduced. If 1B taps are chosen, you need a very very long track. More here: PGGB - FAQ
I mention PGGB-RT is 'near real-time', this is because, in reality, it is doing exactly what the offline upsampling is doing except using memory not disk. It reads in a whole track into memory, does the upsampling and spits out the whole track into memory. It does not work like a typical DSP which has to wait in real-time to collect the necessary samples and then process, this would cause too much delay. For this reason, in foobar PGGB does not appear as a DSP but rather as a decoder under 'tools'.
So the real delay is the time taken to process the first track and this is possible because PGGB-RT always has access to whole tracks on disk. The results are the same as what you have already seen with the offline PGGB upsampled files.
When you have a playlist in foobar and hit play, there will be a delay equal to what it takes to process the first track, but this delay depends both on length of the track and also the CPU speed, generally a few seconds to a few 10 seconds. I use Intel IPP and also make use of multiple cores so the computation is quite efficient. While the first track is playing, PGGB-RT will start processing the second track so by the time the first track is done playing, the second track is already processed and is in memory, ready to be played.
Though streaming is not currently supported, most streaming apps have access to full tracks (at least for Qobuz and Tidal), so the same concept can be applied there too.
Regards,
-ZB
I received the below email from ZB this morning. It regards our thread discussion on the PGGB-RT playback latency.
================================================
I saw some questions raised regarding tap length and delays and feasibility of doing the upsampling (or downsampling) in real-time.
The tap lengths are the maximum PGGB will use but they are not used all the time if the length of the track is not long enough. The taps are for the output rate. So choosing 2M and setting an output rate of 88.2kHz implies a maximum of 2M taps would be used at 88.2kHz and the track length has to be longer than or equal to 2M at the output rate, else the number of taps used will be reduced. If 1B taps are chosen, you need a very very long track. More here: PGGB - FAQ
I mention PGGB-RT is 'near real-time', this is because, in reality, it is doing exactly what the offline upsampling is doing except using memory not disk. It reads in a whole track into memory, does the upsampling and spits out the whole track into memory. It does not work like a typical DSP which has to wait in real-time to collect the necessary samples and then process, this would cause too much delay. For this reason, in foobar PGGB does not appear as a DSP but rather as a decoder under 'tools'.
So the real delay is the time taken to process the first track and this is possible because PGGB-RT always has access to whole tracks on disk. The results are the same as what you have already seen with the offline PGGB upsampled files.
When you have a playlist in foobar and hit play, there will be a delay equal to what it takes to process the first track, but this delay depends both on length of the track and also the CPU speed, generally a few seconds to a few 10 seconds. I use Intel IPP and also make use of multiple cores so the computation is quite efficient. While the first track is playing, PGGB-RT will start processing the second track so by the time the first track is done playing, the second track is already processed and is in memory, ready to be played.
Though streaming is not currently supported, most streaming apps have access to full tracks (at least for Qobuz and Tidal), so the same concept can be applied there too.
Regards,
-ZB
Last edited:
It seems this thread hasn't been been frequented lately, however, I am tempted to purchase it. I have had the pleasure to listen to some PGGB treated albums and I feel I would like to have this software on my computer. I wonder if I should approach ZB via here to obtain the 50% discount? What do you guys think?
You should give me your money and listen to soxr-upsampled files instead, which is free in itself. Kudos to FOSS! 🍻
Just kidding, do, as you please 😁
Just kidding, do, as you please 😁
Since our original thread concluded a number of months ago, you’ll need to contact ZB, author of the PGGB software, to inquire about diyAudio member current pricing. In addition to the maximum performing fee-license PGGB product, ‘remastero’ also offered a no-cost-license product which is a somewhat more limited version of the PGGB as a Foobar2000 plug-in. I’ve no idea whether or not the no-cost-license for the plug-in is still their policy.
There is a link in my post #1 above, to the ‘remastero’ website for more PGGB product information. ZB lists his email as: zb.pggb@gmail.com
Last edited:
Ive been using PGGB with the Foobar plugin and for me its sounds very good.
Ive compared it with SOX in Foobar using this great DSP that allows the filter parameters to be dialled in for eg great impulse response:
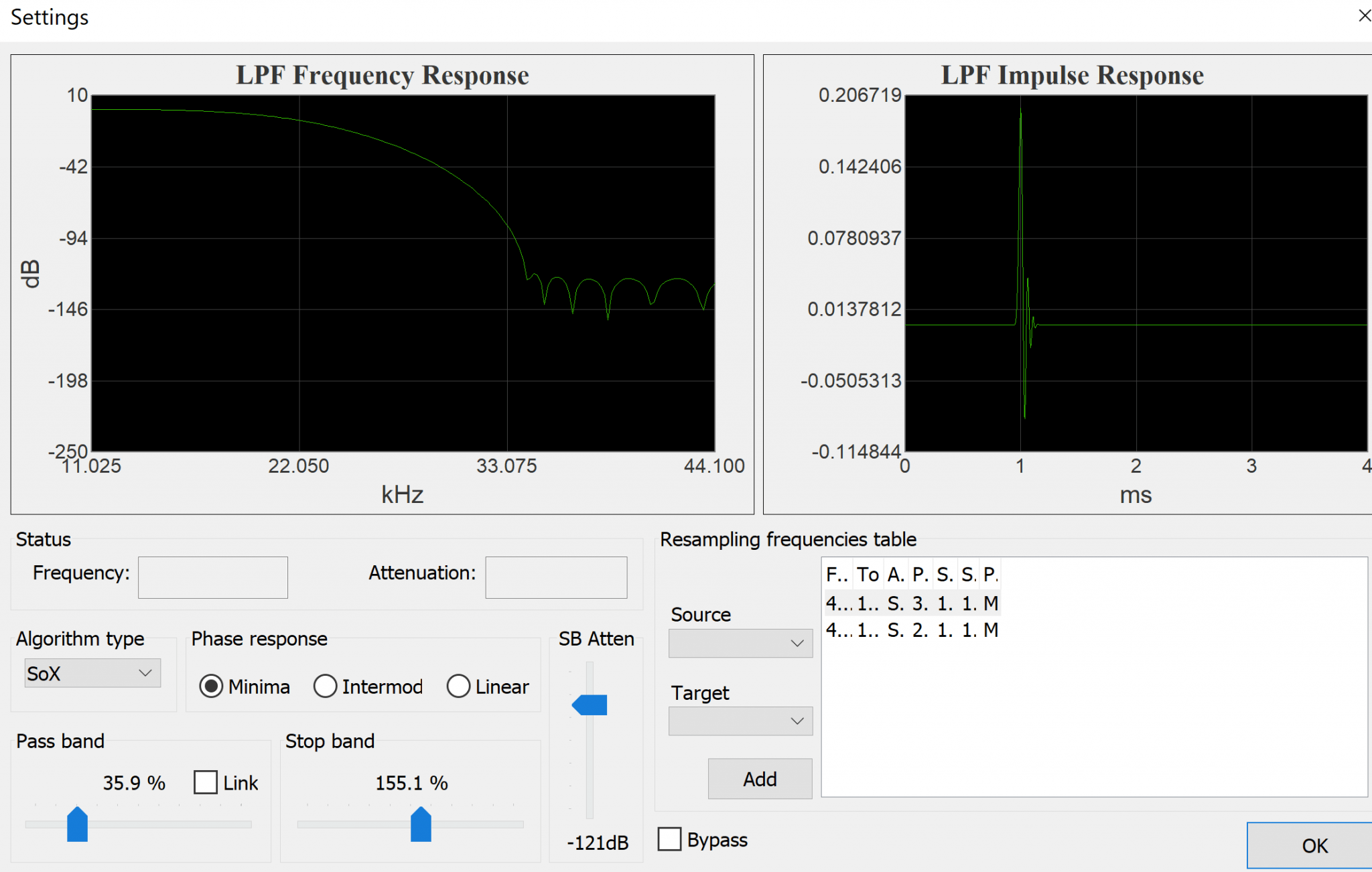
Im mostly using PGGB. Its doing something good for me.
Ive compared it with SOX in Foobar using this great DSP that allows the filter parameters to be dialled in for eg great impulse response:
Im mostly using PGGB. Its doing something good for me.