Bear with me I'm trying to get a handle on basic tube math.
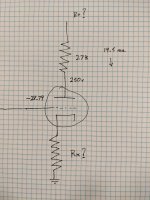
I would be eternally grateful if someone can guide me on the algebra needed to solve this diagram for the unknown B+ and Rk values.
Assuming I know the following static DC values as shown:
250V at the plate
27K Rp
-28.79 grid bias
19.5 ma through the tube
What is the algebra to determine what my B+ and Rk should be to arrive back at these same values? And solve it.
I would assume you have to first solve the B+ then use that to solve the Rk?
Why am I doing this? My load line tool is able to let me try many different plate resistors, plate voltages and currents by just dragging a dot around, easy-peasy. In doing so it gives immediate read out of the NegV on the grid, distortion, Vout, Pout etc. But it doesnt give me a direct reading of what B+ or Rk I'd need to actually build something at that operating point.
So I need to learn how to back into those two values (B+ and Rk) given these four known values, and hoping for some algebra help.
I would be eternally grateful if someone can guide me on the algebra needed to solve this diagram for the unknown B+ and Rk values.
Assuming I know the following static DC values as shown:
250V at the plate
27K Rp
-28.79 grid bias
19.5 ma through the tube
What is the algebra to determine what my B+ and Rk should be to arrive back at these same values? And solve it.
I would assume you have to first solve the B+ then use that to solve the Rk?
Why am I doing this? My load line tool is able to let me try many different plate resistors, plate voltages and currents by just dragging a dot around, easy-peasy. In doing so it gives immediate read out of the NegV on the grid, distortion, Vout, Pout etc. But it doesnt give me a direct reading of what B+ or Rk I'd need to actually build something at that operating point.
So I need to learn how to back into those two values (B+ and Rk) given these four known values, and hoping for some algebra help.
B+ = 250 + 27000x0.0195 = 776.5v
Rk = 28.79/0.0195 = 1476 ohms assuming grid is at 0v
Not a very practical operating point😉
Rk = 28.79/0.0195 = 1476 ohms assuming grid is at 0v
Not a very practical operating point😉
Givens…
This is harder, since the EG is a negative voltage, and the tube's datasheet isn't given. Whatever value of RK, it will force the grid (as far as the catnode is concerned) to look even more negative than the –28.79 volts given.
Thus without knowing the valve (and looking up its datasheet, to see what the transconductance curves are), one can't really determine RK with any convincing authority.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
EA = 250.0 V
RA = 27 kΩ
EG = –28.79 V
IA = 19.5 mA[/sub]
So, using some basic electronics mathRA = 27 kΩ
EG = –28.79 V
IA = 19.5 mA[/sub]
E = IR
E = 27 kΩ × 1,000 Ω/kΩ × 19.5 mA × 0.001 mA/A
E = 526.5 V
andE = 27 kΩ × 1,000 Ω/kΩ × 19.5 mA × 0.001 mA/A
E = 526.5 V
B+ = EA + ERA
B+ = 250 + 526.5
B+ = 776.5 V
Now for the RKB+ = 250 + 526.5
B+ = 776.5 V
This is harder, since the EG is a negative voltage, and the tube's datasheet isn't given. Whatever value of RK, it will force the grid (as far as the catnode is concerned) to look even more negative than the –28.79 volts given.
Thus without knowing the valve (and looking up its datasheet, to see what the transconductance curves are), one can't really determine RK with any convincing authority.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
Thanks! I know its not practical its a transmitting tube (1626 triode) and I just picked a random resistor and spot out of my butt. I'll try this with some known good operating points on other tubes for practice. I was sort of on this track but wasn't adding the 250V back again and messing up.
I really appreciate it, I'm finally beginning to get some baby step traction on learning load lines.
Thanks! I kind of suspected I'd see you answering here GoatGuy! 🙂.
It is a 1626 transmitting triode a very cute little ST tube:
https://frank.pocnet.net/sheets/049/1/1626.pdf
Here is the curve trace of the actual tube taken live, and the parameters I entered (27K @ 250V @ 19.5 ma). The math works! The chart only goes to 500V but as you can see by the angle of the load line that it will be terminating somewhere in that > 700V range at 0 ma. I hope I'm interpreting this right.
In practicality to use this tube as a voltage amp with a more practical and safer B+ (maybe 400V), I'd have to make the load line steeper (decrease resistor) and/or decrease the plate voltage (move the dot farther left) and/or decrease the ma (move the dot down)?
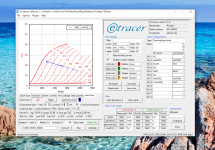
In practicality to use this tube as a voltage amp with a more practical and safer B+ (maybe 400V), I'd have to make the load line steeper (decrease resistor) and/or decrease the plate voltage (move the dot farther left) and/or decrease the ma (move the dot down)?
Last edited:
Well, there you are. A datasheet! Will wonders never cease.
So, here's what I do when trying to 'home in' on a steady-state solution. Look at the upper set of curves. First, assume the EK is '0' or ground, so that the ΔEA-K is exactly 250 volts. (We'll adjust later). To get a current of 19 mA requires something between EG –32 and –40 volts. The given grid bias is already –28.8 V, so going with the median of –36 volts, that's what, another 7 volts or so.
Close enough. EK then needs to be ⊕7 V above ground. Again using
There you go!
⋅-=≡ GoatGuy ✓ ≡=-⋅
So, here's what I do when trying to 'home in' on a steady-state solution. Look at the upper set of curves. First, assume the EK is '0' or ground, so that the ΔEA-K is exactly 250 volts. (We'll adjust later). To get a current of 19 mA requires something between EG –32 and –40 volts. The given grid bias is already –28.8 V, so going with the median of –36 volts, that's what, another 7 volts or so.
Close enough. EK then needs to be ⊕7 V above ground. Again using
E = IR
7 = (0.0195 A) • RK
RK = 7 ÷ 0.0195 → about 360 Ω.
OK! Noiw is it “worth correcting” for the 250 - 7 or 243 volt EA-K voltage? No, not really. This valve has pretty soft curves, so the approximation is just fine. Not so, if you were using a 12AX7 or 6SN7 or other much 'gain-i-er' tube. 7 = (0.0195 A) • RK
RK = 7 ÷ 0.0195 → about 360 Ω.
There you go!
⋅-=≡ GoatGuy ✓ ≡=-⋅
The plate voltage is relative to the cathode, so for cathode bias, B+ needs to be increased by the cathode voltage.
B+ = 0.0195 * 27 000 + 250 + 29 = 806V
B+ = 0.0195 * 27 000 + 250 + 29 = 806V
needs to be increased by …
I disagree: it is not how voltages are listed in schematics. Rather, voltages are almost always referenced to ground as the '0 volt' value unless specified between 2 measurement points.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
I disagree: it is not how voltages are listed in schematics. Rather, voltages are almost always referenced to ground as the '0 volt' value unless specified between 2 measurement points.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
The plate voltages shown in tube curve characteristic charts are relative to the cathode. The curves are then independent of the cathode voltage. If you pick an operating point (plate voltage) from the curves, the actual plate voltage to ground in the circuit must account for any cathode voltage.
Right you are.
Yes, and no (with your wording): the curves show operating point of the (VA - VK) current relative to VK - VG 'grid' bias point difference.
Yes, that is so. But one does not write '250 V' on the diagram adjacent to the plate, and have that mean 'relative to cathode'. It means 'relative to ground', as vexing as that is to compute.
Moreover, (agreeing with you), when one picks a VA voltage (like '+250' in this example), one must take into account the increased cathode voltage imposed by the RK cathode auto-bias resistor.
If you read again my example calculation, note that I used not one, but two set-points in utilizing the curve data. The stated VA of +250, the not stated VK cathode, the current for all intents and purposes being IA ≡ IK, and the intersection on the chart of a current of about 19 mA with a plate of about 250, requiring a VG bias of about –36 V … relative to cathode.
Since the voltage of –28.8 VG was printed on the diagram, I assumed it was a measured value. Hardly seems like the theoretical value, since –28.8 VG relative to VK would not result in 19.5 mA flowing thru the valve at VA being around 250 V.
Therefore, the VK has to be higher than VGND, increasing the relative negative voltage of VG → VK.
(–28.8 V minus about 7 V) gives –36 V., which matches the spot on the data sheet curves corresponding to the 19 mA.
I've grown pretty adept at this kind of real-circuit squishiness … because I have taken the time and “burned my fingers” measuring a whole lot of circuits I've both designed, and been tasked to repair. And 'tube roll' for friends. That, and I still love mathematics, as opaque as it sometimes can be.
Thank you for your continued discussion.
⋅-=≡ GoatGuy ✓ ≡=-⋅
Last edited:
I'm beginning to not understand, thats ok. but the negative grid voltage came right from the calculator in etracer, post #7.
Windcrest77,
I know nothing about an etracer.
But most curve tracers do not use self bias in the circuit.
They use fixed bias in the circuit.
So . . .
You are probably talking about Fixed Bias (-) that comes from the etracer to the grid.
In that case, the cathode is at ground ('ground' being the B+ return).
And the Fixed Bias return (+) is also returned to the B+ return (again 'ground').
That is how it is when there is no self bias resistor in the circuit.
Does that explain it?
I know nothing about an etracer.
But most curve tracers do not use self bias in the circuit.
They use fixed bias in the circuit.
So . . .
You are probably talking about Fixed Bias (-) that comes from the etracer to the grid.
In that case, the cathode is at ground ('ground' being the B+ return).
And the Fixed Bias return (+) is also returned to the B+ return (again 'ground').
That is how it is when there is no self bias resistor in the circuit.
Does that explain it?
Last edited:
Yes that makes sense, the device does ground the cathode and I assume pulses the grid across each plate voltage increment. The tab I'm displaying in post 7 is not the trace tab, its the load line tab that uses the curves just obtained from the trace.
My favorite tube tester are my amplifiers.
The first time I built a stereo single ended 45 amplifier, it sounded great!
I had just finished it, and I listened from 12 midnight, until 2:00 in the morning.
Then I turned it off. The next morning, about 10:00, I turned it on, and it screamed at me.
One of the NOS 45 tubes was glowing from gas, and that made the amplifier a good tube tester (it showed a bad one).
The first time I built a stereo single ended 45 amplifier, it sounded great!
I had just finished it, and I listened from 12 midnight, until 2:00 in the morning.
Then I turned it off. The next morning, about 10:00, I turned it on, and it screamed at me.
One of the NOS 45 tubes was glowing from gas, and that made the amplifier a good tube tester (it showed a bad one).
GoatGuy- what software are you typing your equations with? Or, are you typing in Word and cutting/pasting?
Just wondering...
Just wondering...
Thanks. So the B+ calculation is pretty reliable but Rk is tricky. I can even nearly get Bb+ visually by extending the load line down to 0 ma on the right. But for a 65 year old limited-math limited-time hacker like me, I look for a repeatable process even if that means strapping up a quick circuit and doing trial and error...
So if I use my loadline calculator here to quickly and brainlessly come up with an operating point I like distortion-wise, gain-wise, power-wise, because I have direct readout for an exact tube I just scanned... I'll have reliable values for B+, Ea, Ra, Eg and Ia! I can then calculate a ballpark Rk even if thats just doing Eg / IA and strap up the circuit with a rheostat for Rk that is near mid rotation for that value (I have a collection of 15 different Ohmite 25W rheostats). Then just turn the rheostat while measuring for Eg to hit the target I obtained on my easy-peasy loadline calculator? Or should I be trying to hit 19.5 MA instead with rotating the rheostat? Then all I'd have to do is replace it with a fixed resistor.
I know this sounds like a rude and crude way to do it, but why were resistor substitution boxes considered to be "essential gear" in the 1950's but today nobody needs a resistor substitution box? And why did so many regular "dads" dabble in kits and Tubes in the 1950's who I'm sure didn't have as great a handle on the math and certainly no sim, just loadlines. I would think resistor substitution would have been standard operating procedure for those hobbyists back then?
Last edited:
What is your actual circuit? Is it a combination of grid bias and self bias, or is it strictly self bias with just a cathode resistor and no negative voltage applied to the grid?
No other negative voltage applied...
Knowing my B+, Ea, Ra, Eg and Ia already...
My goal is to learn how to calculate or discover through breadboarding how to determine the Rk value in order to do simple self bias. Where that Rk value will be the value that will best retain the operating point of the B+, Ea, Ra, Eg and Ia I already know I want. To determine the last missing value (Rk) needed to build that voltage stage as self bias grounded Cathode stage. By math or experimentation / substitution, either method would be fine.
Last edited: