Easy, in to a resistive load. Maybe, not so easy if the load exhibits significant capacitive reactance.
If the bandwidt of the signal is 20kHz, you will never have any higher frequency components, cymbal or rim shot or anything else. It may look to you like a square wave, but when bandlimited to 20kHz, that's the highest frequncy component that is in the signal.
Jan
Yes, 20kHz is the highest frequency component in the signal after you do a Fourier on it. But that is not the question. The question is: "what is the highest slew-rate of the original sound?" And the slew-rate of a signal composed of sines can be higher than that of the highest frequency making it up. That is the reason that for measuring something like a square wave with a scope, your scope needs at least 3 to 5 times the (steady state) bandwidth of the fundamental.
I seem to remember there have been some studies into creating the fastest possible slew-rate starting from a spectrum. But I cannot remember where.
Problem is when go into "sound", then you have to consider what is the maximum compression rate you can give to air before you go into the non-linear zone of the curve. Because you could argue you go into slew-limitation of air. From a JAES article (vol 13 n°3) about a horn driven with compressed air, they got to somewhere near 140dB at some 60Hz before the "sound" got distorted because the air became non-linear.
I seem to remember there have been some studies into creating the fastest possible slew-rate starting from a spectrum. But I cannot remember where.
Problem is when go into "sound", then you have to consider what is the maximum compression rate you can give to air before you go into the non-linear zone of the curve. Because you could argue you go into slew-limitation of air. From a JAES article (vol 13 n°3) about a horn driven with compressed air, they got to somewhere near 140dB at some 60Hz before the "sound" got distorted because the air became non-linear.
I assumed the OP was interested in recorded signals.You only need to worry when doing live recording. The usual bandwidth limiter is the microphone and it sets max slew until your A/D and its anti-aliasing filters.
'Real life' max slew are with clap sticks and drum rim shots. But these are incredibly difficult to record without overloading, microphone & A/D. The good news is that you usually can't hear these overload on a good microphone & recorder.
If so, max slew depends on Bandwidth & Level ... fancy maths by Tom et al.
Bats have very high bandwidth but I'm not sure there's any situation where we have high levels too
Cymbals and jangling keys have very high bandwidths but the transients with clap sticks & drum rim shots usually give higher slews cos they usually overload the recording system.
Microphones should set the Bandwidth, Level & hence slew in a good recording system at least until the A/D anti-aliasing filters.
Nope. This is a popular misconception among people who don't "do-the-math". No combination of frequencies that does not clip the amplifier has a higher slew rate than the highest frequency with an amplitude near clipping, Vp. Granted, an amp that has just enough slew to avoid slew limiting is probably not great THD, so a slew margin of 2x or more is wise. However, making other compromises for the sake of unnecessary slew is a bad idea.
Exactly.
Math is useful for figuring out how much (or little) you need. Engineering (and experience) is useful for figuring out how close you want to get to the minimum/maximum determined by math in the design. A good design is the result of multivariate optimization. There may be many good solutions to an engineering problem ... or no good solutions.
Tom
Math is useful for figuring out how much (or little) you need. Engineering (and experience) is useful for figuring out how close you want to get to the minimum/maximum determined by math in the design. A good design is the result of multivariate optimization. There may be many good solutions to an engineering problem ... or no good solutions.
Tom
Bats have very high bandwidth but I'm not sure there's any situation where we have high levels too
Cymbals and jangling keys have very high bandwidths but the transients with clap sticks & drum rim shots usually give higher slews cos they usually overload the recording system.
There is no recording system in the thread starter's question, according to posts #22 and #30, https://www.diyaudio.com/community/threads/maximum-typical-slew-rates-in-audio.403357/post-7454692 and https://www.diyaudio.com/community/threads/maximum-typical-slew-rates-in-audio.403357/post-7454927
For what it's worth, my frequency-divider-based bat detector detects my jangling keys up to about 3 m distance and the bats in my neigbourhood up to about 20 m. It uses a MEMS microphone that was designed for humans, so its bandwidth is not very good.
Here is an understanding of the phenomenon. The required Slew Rate is determined by at least two requirements:
1. the frequency band and this can be easily calculated and has already been explained by colleagues above and the requirements from this point of view are very relaxed and can be satisfied very easily with the current components and a correctly designed schematic.
2. the intermodulation distortions that are generated due to the negative reaction, and from this point of view a very high slewrate is needed. In fact, the input-output transition time is the one that matters more, but it is closely related to the slew rate.
1. the frequency band and this can be easily calculated and has already been explained by colleagues above and the requirements from this point of view are very relaxed and can be satisfied very easily with the current components and a correctly designed schematic.
2. the intermodulation distortions that are generated due to the negative reaction, and from this point of view a very high slewrate is needed. In fact, the input-output transition time is the one that matters more, but it is closely related to the slew rate.
OP used the term slew rate but asks for a natural phenomen. Slew rate exists in electronics where there is a "volt" around. In nature, which this seem to be about, there is no "volt" so no slew rate. But there is spectral content so you just have to make up your mind of what is the highest frequency you like to pose the question for and then the steepness of the signal is known. You also use the term "audio" in your question, begging for a "gear" answer but are disappointed people talk about gear
The way one asks, one shall be answered...
//
The way one asks, one shall be answered...
//
I think these posts are missing practicalities - what an entire amp needs to achieve for good distortion characteristics. As it's handy I chose JLH's class A. It's not just slew rate really in the terms that have been mentioned in posts.
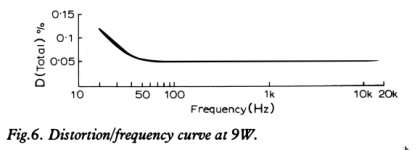
Taking the TL072H distortion is low with a gain of 10, 1Vrms out and and an input impedance of 1k. Slew rate typ 20v/uSec. With a 40v supply. Bandwidth with a gain of 10 is similar to JLH's.
Higher spec amp's - bandwidth goes up.
Slew rate at 80kHz is 4 times that at 20kHz.
Whoops may have added one image twice.
Taking the TL072H distortion is low with a gain of 10, 1Vrms out and and an input impedance of 1k. Slew rate typ 20v/uSec. With a 40v supply. Bandwidth with a gain of 10 is similar to JLH's.
Higher spec amp's - bandwidth goes up.
Slew rate at 80kHz is 4 times that at 20kHz.
Whoops may have added one image twice.
http://nwavguy.blogspot.com/2011/08/op-amp-measurements.html
Slew Rate – Here’s another huge myth: The faster the slew rate the better. But the fastest “slew” you can get from a 16/44 digital recording has a period of about 22 uS. So the O2, worst case, needs to slew 20 volts in 22 uS or a slew rate of 0.9 V/uS. And even considering those rare 24/96 recordings, the requirement is still 1.8 V/uS. SACD or 24/192, in theory, could require about 3.6 V/uS but, in practice, never will as that would be a 0 dBFS signal close to 100 Khz. Such a signal would never make it through the recording chain, and if it did, would fry tweeters and cause bats to fly into the side of your house. The peak levels in music generally fall as the frequency rises. This is especially true at ultrasonic frequencies. If you think I’m wrong, please reference a recording than can challenge even a 1.5 V/uS headphone amp. The industry rule of thumb, even on the recording side of the signal chain, is 0.2 V/uS per volt RMS of maximum output. I’ve doubled that just to be ultra conservative so 7*0.4 = 2.8 V/uS for the O2’s requirement. As I have explained elsewhere,slew rates well in excess of what’s needed come at a price. Somewhere in the range of 2.5 – 5 V/uS is ideal for a high output headphone amp like the O2.
Hope this answers your original question
Slew Rate – Here’s another huge myth: The faster the slew rate the better. But the fastest “slew” you can get from a 16/44 digital recording has a period of about 22 uS. So the O2, worst case, needs to slew 20 volts in 22 uS or a slew rate of 0.9 V/uS. And even considering those rare 24/96 recordings, the requirement is still 1.8 V/uS. SACD or 24/192, in theory, could require about 3.6 V/uS but, in practice, never will as that would be a 0 dBFS signal close to 100 Khz. Such a signal would never make it through the recording chain, and if it did, would fry tweeters and cause bats to fly into the side of your house. The peak levels in music generally fall as the frequency rises. This is especially true at ultrasonic frequencies. If you think I’m wrong, please reference a recording than can challenge even a 1.5 V/uS headphone amp. The industry rule of thumb, even on the recording side of the signal chain, is 0.2 V/uS per volt RMS of maximum output. I’ve doubled that just to be ultra conservative so 7*0.4 = 2.8 V/uS for the O2’s requirement. As I have explained elsewhere,slew rates well in excess of what’s needed come at a price. Somewhere in the range of 2.5 – 5 V/uS is ideal for a high output headphone amp like the O2.
Hope this answers your original question
I have only looked at the digital side recently. DSP's The input levels appear to be 1v rms. Slew rate 0.126v/uSec at 20k. This particular one is also analogue out. What happens. The hf is way above audio so it's filtered out. Distortion depends on how accurately it's digitised and converted back. The BBC did work on the bit levels needed yonks ago. Blind testing with a variety of well educated ears.
A class D amp amplifies these pulses. The output signal is bigger, the hf is filtered out. % wise distortion is still the same as the initial digitised recording - other than failings in it's performance and losses on the way to conversion..
The analogue world. A typical TL072H will just about meet it's 20k distortion spec with a gain of 10. 1volt rms out and a 40v supply. It wont with gains above that This has a far greater feedback factor than J:LH's amp. That mean as always that distortion before feedback is important. In both cases a bandwidth of ~5 times the audio bandwidth is needed to maintain the performance. That appears to be typical of higher performance analogue designs.
A class D amp amplifies these pulses. The output signal is bigger, the hf is filtered out. % wise distortion is still the same as the initial digitised recording - other than failings in it's performance and losses on the way to conversion..
The analogue world. A typical TL072H will just about meet it's 20k distortion spec with a gain of 10. 1volt rms out and a 40v supply. It wont with gains above that This has a far greater feedback factor than J:LH's amp. That mean as always that distortion before feedback is important. In both cases a bandwidth of ~5 times the audio bandwidth is needed to maintain the performance. That appears to be typical of higher performance analogue designs.
Still very easy on typical speaker. Just add more output transistors. In VFA, slew rate depend on LTP current and the compensation. In CFA, it more easy to achieve high slew rate.
If you want to low distortion in high frequency, use 2 or more pole compensation. Several member here demonstrated how to achieve very low distortion at 20kHz. So I think, very low distortion at high frequency and very high slew rate are not the problem, except you are a novice at designing an audio amplifier.