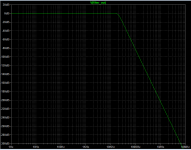
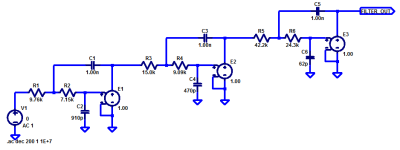
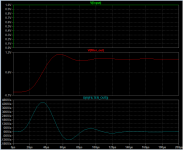
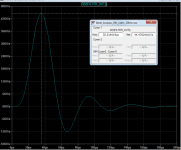
regarding the simulation described in post #40: it can be calculated by hand more easily.
20 kHz --> TAU = (1 / (2 * pi * freq)) = 7.958 usec
V(t) = Amplitude * (1 - exp(-t/TAU))
derivative of V(t) = dV/dt = (Amplitude / TAU) * exp(-t/TAU)
dV/dt is highest at t=0. Plugging in numerical values for Amplitude, TAU, and t :
dV/dt = (1.00 / 7.958E-6) * exp(0) = 1.257E+5 volts/second = 0.1257 volts/usec = 125.7 mV/usec
no simulator required.
20 kHz --> TAU = (1 / (2 * pi * freq)) = 7.958 usec
V(t) = Amplitude * (1 - exp(-t/TAU))
derivative of V(t) = dV/dt = (Amplitude / TAU) * exp(-t/TAU)
dV/dt is highest at t=0. Plugging in numerical values for Amplitude, TAU, and t :
dV/dt = (1.00 / 7.958E-6) * exp(0) = 1.257E+5 volts/second = 0.1257 volts/usec = 125.7 mV/usec
no simulator required.
Last edited:
Thanks, I know that. Just thought for some a simulation might be easier to understand. Good to do it both ways. In the past I always did a circuit design by hand calculation. Then I would give the design to a junior to simulate. They would consider it magic how close my calculations came to sym results. Often no rework was needed. Designs came back from prototype and just worked.
When you have a step from -V to +V, the initial rate of change after a first-order filter with time constant RC will be 2V/(RC) rather than V/(RC). In any case, I don't see what it has to do with the question how large the rate of change of practical acoustical signals can be.
The answer is: This calculations show the upper limit of possible slew rate in real audio. Musical or other audio events may produce quite different slewrates, but never will these exceed the boundaries given by 20kHz bandwidth. There are many hints for being them far below that limits - except some German marching music. Honestly, I never missed that too much 😉
The point is that all real signals are band limited. Pick the limit you want to impose. For audio it’s generally well accepted that 20 kHz is a practical limit for bandwidth. Even if you chose 40 kHz the slew calculated eariler would only double. The step includes the band limit and everything below it to generate the fastest band limited slew that’s possible for that bandwidth.
If I understand the thread starter's question correctly, which is a big if as the question still isn't entirely clear to me, he is interested in the rate of change of practical acoustical signals. That can be the echolocation signal of a bat. Bats are anything but band limited to 20 kHz.
This is certainly true - but not relevant to us humans with our band limited hearing capabilities. Admittedly I do not focus on audio equipment for bats.
I repeated this experiment except I simulated a six pole Butterworth lowpass filter with a 20 kHz corner frequency. For simplicity of simulation I chose a Sallen-Key implementation, and I used ideal unity gain buffers (spice "E" devices) having infinite bandwidth and infinite input impedance.
As you can see, with a 1V step input, the six pole filter's step response hits a maximum slew rate of 44.5 volts per milllisecond , which equals 44.5 millivolts per microsecond, i.e. 0.0445 volts per microsecond. The Butterworth "maximally flat" criterion looks like it was met.
_
Attachments
Agreed! In this context not only the bandwidth but also the magnitude and the respective behaviour of compressed air will be relevant. I am thinking of atomic explosions, for example.
I think we need a clearer question.
@HalFoster
Are you interested in the peak rate of change of practical acoustical signals, or is that just my misinterpretation?
Is it the peak rate of change as such that matters, or rather the ratio of the peak rate of change to the peak sound pressure?
Are there any constraints on the sounds? For example, which of these are relevant to you:
-Marching music
-Gamelan music
-Bats
-Mice
-Conventional bombs
-Atomic bombs
-Cannon shots (those are used in music sometimes)
-Medical ultrasound equipment
@HalFoster
Are you interested in the peak rate of change of practical acoustical signals, or is that just my misinterpretation?
Is it the peak rate of change as such that matters, or rather the ratio of the peak rate of change to the peak sound pressure?
Are there any constraints on the sounds? For example, which of these are relevant to you:
-Marching music
-Gamelan music
-Bats
-Mice
-Conventional bombs
-Atomic bombs
-Cannon shots (those are used in music sometimes)
-Medical ultrasound equipment
I agree with @MarcelvdG here.
The question as posed reads to me like "what is the slew rate of the sound that has the fastest rise time?" (Except that specific numbers were requested)
So far, informed commentators have referenced the slew rate of a 20Khz sine wave. Of course the concept of "slew rate" as we know it applies to electrical signals and as such we have to get the signal from the analogue sound pressure domain into an electrical signal. This step requires a transducer, of course a microphone in this case, and it will have a corresponding pre-amplifier that will be bandwidth and hence slew rate limited by the input filter. Thus we are back to 20Khz sinewaves as soon as we move from the sound pressure domain to the electrical domain.
IIRC correctly Douglas Self did do some experiments looking at recorded music and did not find any recordings with unusually high slew rate regardless of musical genre. I think Hal was looking to avoid recorded music as the source for this, however I'm not sure that is a valid exclusion in the sense that any high quality audio equipment should be able to reproduce with exceptional accuracy any signal , be it from a live stage performance or from a recording of that event.
I understand that this may feel deeply unsatisfying as intuitively it is easy to imagine that a snare hit or cymbal crash must surely have a spectacular transient at the beginning, but in reality anything over 20Khz in terms of its spectral bandwidth won't be heard by typical humans and will get filtered out of most audio equipment pretty quickly.
It may of course be possible using s special high frequency transducer and a very high bandwidth amplifier such as you may find in your 'scope input stage along with a very fast ADC (again like your 'scope) to actually measure such a sound and see if there really is a super fast transient but I'm not altogether sure what you would do with that information 🙂 apart from to say "I knew it!".
Anyway - I'm done for today as it getting rather late here.
The question as posed reads to me like "what is the slew rate of the sound that has the fastest rise time?" (Except that specific numbers were requested)
So far, informed commentators have referenced the slew rate of a 20Khz sine wave. Of course the concept of "slew rate" as we know it applies to electrical signals and as such we have to get the signal from the analogue sound pressure domain into an electrical signal. This step requires a transducer, of course a microphone in this case, and it will have a corresponding pre-amplifier that will be bandwidth and hence slew rate limited by the input filter. Thus we are back to 20Khz sinewaves as soon as we move from the sound pressure domain to the electrical domain.
IIRC correctly Douglas Self did do some experiments looking at recorded music and did not find any recordings with unusually high slew rate regardless of musical genre. I think Hal was looking to avoid recorded music as the source for this, however I'm not sure that is a valid exclusion in the sense that any high quality audio equipment should be able to reproduce with exceptional accuracy any signal , be it from a live stage performance or from a recording of that event.
I understand that this may feel deeply unsatisfying as intuitively it is easy to imagine that a snare hit or cymbal crash must surely have a spectacular transient at the beginning, but in reality anything over 20Khz in terms of its spectral bandwidth won't be heard by typical humans and will get filtered out of most audio equipment pretty quickly.
It may of course be possible using s special high frequency transducer and a very high bandwidth amplifier such as you may find in your 'scope input stage along with a very fast ADC (again like your 'scope) to actually measure such a sound and see if there really is a super fast transient but I'm not altogether sure what you would do with that information 🙂 apart from to say "I knew it!".
Anyway - I'm done for today as it getting rather late here.
Agreed, I would be willing to bet a cymbal crash would be loaded with ultrasonics that could be recorded with specialized recording equipment. So yes a beter question is in order. For audio, it's important to band limit signals so that things like ultrasonics, noise , and EMI do not excite nonlinearities in the subsequent circuitry.
Would a complete end to end "ideal" audio recording and playback system with 1 MHz bandwidth sound better? Quite doubtful for humans. But I never heard one, so who knows.
Would a complete end to end "ideal" audio recording and playback system with 1 MHz bandwidth sound better? Quite doubtful for humans. But I never heard one, so who knows.
Seen recent threads with research related to distortion analysis
and multiple tone analysis.
Rather theoretical or real often a argument I'm sure.
Far as I remember around 20 to 30V/us
considered to eliminate the distortion.
Is comforting to know with calculations people have shown. How low
the required slew rate is.
Assuming that is single tone sine wave used for the formula.
With complicated waveforms and wider range
of harmonic content. Then more slew rate wouldn't hurt, Seems
logical at least.
Im all for fastest slew as possible.
Assuming there is a theoretical limit to currently available power devices.
I have seen numerous numbers mentioned as the limit.
Interesting the mentioned slew limits of recorded music using microphones.
And having seen/heard some rather intense waveforms which
direct recording or electronic synthesis can produce. Being fan of more
aggressive ambient or experimental electronic music. Seems
high slew rate would be very beneficial for electronic.
Possibly combination would be high level of transient or
speed described by horn loaded systems combined with
high slew amplifier. And even planar or ribbons
and multiple tone analysis.
Rather theoretical or real often a argument I'm sure.
Far as I remember around 20 to 30V/us
considered to eliminate the distortion.
Is comforting to know with calculations people have shown. How low
the required slew rate is.
Assuming that is single tone sine wave used for the formula.
With complicated waveforms and wider range
of harmonic content. Then more slew rate wouldn't hurt, Seems
logical at least.
Im all for fastest slew as possible.
Assuming there is a theoretical limit to currently available power devices.
I have seen numerous numbers mentioned as the limit.
Interesting the mentioned slew limits of recorded music using microphones.
And having seen/heard some rather intense waveforms which
direct recording or electronic synthesis can produce. Being fan of more
aggressive ambient or experimental electronic music. Seems
high slew rate would be very beneficial for electronic.
Possibly combination would be high level of transient or
speed described by horn loaded systems combined with
high slew amplifier. And even planar or ribbons
Last edited:
ST datasheets for the TDA2030 mention 8 V/us as the maximum slew rate.
The new Class D amps may be able to withstand a highr slew rate, the speakers are the ultimate barrier.
And your ears' ability to respond, of course.
In real life situations, the driver is the limiter for the maximum rate, as it must flex as fast as needed.
So I think the question was more theoretical than practical.
The OPA 2134 can go above 40 IIRC, but building a matching power section needs expertise, which is not needed in most cases, like using a big SUV to go to the nearest big store.....the 4x4 function is superfluous.
The new Class D amps may be able to withstand a highr slew rate, the speakers are the ultimate barrier.
And your ears' ability to respond, of course.
In real life situations, the driver is the limiter for the maximum rate, as it must flex as fast as needed.
So I think the question was more theoretical than practical.
The OPA 2134 can go above 40 IIRC, but building a matching power section needs expertise, which is not needed in most cases, like using a big SUV to go to the nearest big store.....the 4x4 function is superfluous.
Last edited:
I think it is theoretical question.
So I think the slew rate must be high as possible.
50V/uS in 100W 8 Ohm amplifier is very easy to achieve, why we should limit the slew rate?
Power bandwidth around 200 kHz is very easy to achieve.
So I think the slew rate must be high as possible.
50V/uS in 100W 8 Ohm amplifier is very easy to achieve, why we should limit the slew rate?
Power bandwidth around 200 kHz is very easy to achieve.
It would help if the question was worded somewhat coherently and there was a question mark at the end of the question. For example: "Which musical instrument requires the highest slew rate to reproduce?"
I answered the question, "what is the minimum slew rate required for high fidelity audio reproduction?". My answer more than covers your question.
Marcel answered the question, "which piece of music requires the highest slew rate to reproduce?". You can find his answer in Post #20.
I suspect the clicks and pops in an LP groove are pretty high slew rate too. Is a click or pop an instrument?
I've had similar thoughts. Here's how I view it: The highest rate of change would be to go from the lowest output voltage to the highest within one sample period.
For CD audio at 2 V RMS line level that works out to: SR = 2*Vpeak/ts = 2*Vpeak*fs -> SR = 2*2.82*44100 = 249 kV/s (aka 0.249 V/µs).
For pro audio at 4 V RMS, 192 kHz: SR = 2*sqrt(2)*4*192000 = 2.17 V/µs.
One could argue that this is a bit simplistic as I assume the signal changes linearly from one sample to the next. I would also argue that the signal should more than reach the required voltage. It should be allowed to settle a bit. But still... Even if you bump the numbers up by a factor of 10 you would have no trouble finding an opamp that could reproduce the required output.
It seems pretty clear to to me that audio reproduction is mostly limited by the power amp - at least for slew-rate.
Tom
Yep! Make the amp as close to an ideal amp as possible. Vout = A*Vin. That's it.
Tom
How dare you introduce other variables?! It was a simple question... 🙂
Graceful clipping and overload recovery is another interesting topic.
Tom
Rats are up there too. Their ultrasonic vocalizations extend to 65 kHz. The also seem to use several discrete frequency bands for their communications. The lowest band is just above human hearing. The second band is in the 40-50s kHz. Not thereby said that their hearing covers the continuous spectrum up to 65 kHz.
More here: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4598429/
Is a rat a musical instrument?
🙂 Tom